Objetivo de la Sesin Al concluir esta sesin

Objetivo de la Sesión. Al concluir esta sesión manejaras los principales sistemas de numeración

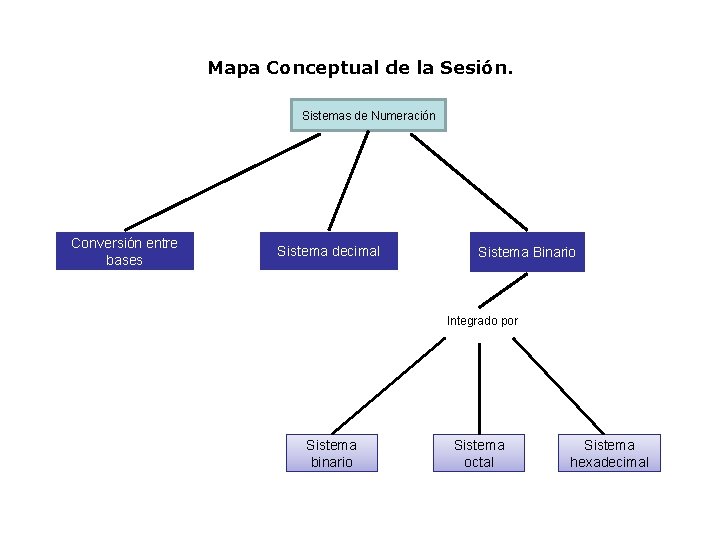
Mapa Conceptual de la Sesión. Sistemas de Numeración Conversión entre bases Sistema decimal Sistema Binario Integrado por Sistema binario Sistema octal Sistema hexadecimal

¿Qué son los sistemas de numeración ? Un sistema de numeración es un conjunto de símbolos y reglas que permiten representar datos numéricos. Los sistemas de numeración actuales son sistemas de tipo posicional, que se caracterizan porque cada elemento tiene valor distinto según la posición que ocupa en la cifra o cantidad representada. MSD – Most Significant Digit (Digito más significativo) LSD – Least Significant Digit (Digito menos significativo)

Sistemas de Numeración Un sistema de numeración en base b utiliza para representar los números un alfabeto compuesto por b símbolos o cifras Ejemplos: b = 10 (decimal) {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} b = 16 (hexadecimal) {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F} b = 2 (binario) {0, 1} El número se expresa mediante una secuencia de cifras: N . . . n 4 n 3 n 2 n 1 n 0 n 1 n 2 n 3. . . El valor de cada cifra depende de la cifra en sí y de la posición que ocupa en la secuencia

¿A que nos referimos conversión entre bases? La forma más comúnmente usada para realizar la conversión entre diferentes bases es utilizando el sistema posicional; el valor significativo asignado a cada digito es una cantidad que está en función de su posición. N = dp 1 np 1 + dp 2 np 2 + … + d 0 n 0 + d (q 1) + d (q 2)n (q 2) Forma compacta N= dini + djn (j) d son los dígitos (coeficientes del número) n la base del sistema P el número de dígitos externos q el número de dígitos fraccionarios El digito más a la derecha se le conoce como menos significativo El dígito más a la izquierda se le conoce como más significativo

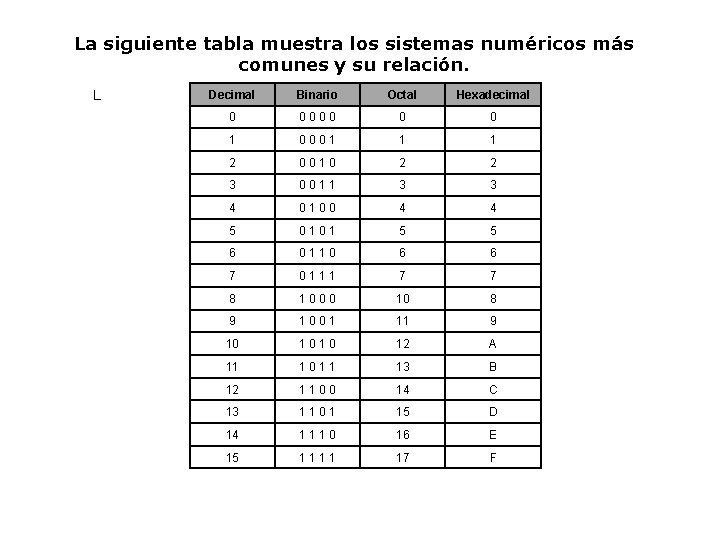
La siguiente tabla muestra los sistemas numéricos más comunes y su relación. L Decimal Binario Octal Hexadecimal 0 0000 0 0 1 0001 1 1 2 0010 2 2 3 0011 3 3 4 0100 4 4 5 0101 5 5 6 0110 6 6 7 0111 7 7 8 1000 10 8 9 1001 11 9 10 1010 12 A 11 1011 13 B 12 1100 14 C 13 1101 15 D 14 1110 16 E 15 1111 17 F

Sistema Decimal Emplea diez diferentes dígitos { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 } Por esto se dice que la base del sistema decimal es diez. Ejemplo. Representar el número 3637. 2510 en forma posicional. Datos: 4 dígitos, p = 4 y 2 dígitos fraccionarios q=2 3637. 25 = di 10 i + dj 10 –(i) = [ 7 x 100 + 3 x 101 + 6 x 102 + 3 x 103 ] + [ 2 x 10 1 + 5 x 10 2 ] = [ 7 x 1 + 3 x 10 + 6 x 100 + 3 x 1000 ] + [ 2/10 + 5/100 ] = [ 7 + 30 + 600 + 3000] + [ 0. 2 + 0. 05 ] = 3637. 25

Conversión de decimal a binario El método para convertir un número decimal a binario es el método de divisiones sucesivas. 1. Dividir el numero decimal entre 2. 2. El residuo (uno o cero) es el dígito menos significativo, el cual se almacena en un arreglo unidimensional. 3. Dividir entre 2 el cociente de la división anterior, pero ahora el residuo se coloca en la siguiente posición de más significativo valor. 4. Repetir el paso anterior y el residuo se coloca en la siguiente posición de más significativo valor. 5. Repetir el paso anterior hasta obtener un cociente cero. 6. Los números en el arreglo unidimensional se muestran de abajo hacia arriba.

Conversión de decimal a binario, ejemplo: 2610 = 110102 0, 187510 = 0, 00112 26, 187510 = 11010, 00112 Fuente: Higinio Mora;

Conversión de decimal a binario, ejemplo: Convertir 17310 a ? 2 173 2 86 1 43 0 21 1 10 1 5 0 2 1 1 0 0 1 17310 = 101011012 Convertir 312910 a ? 2 3128 2 1564 1 782 0 391 0 195 1 97 1 48 1 24 0 12 0 6 0 3 0 1 312910 = 1100001110012

Conversión de decimal a Octal Primer Método. [ ]10 [ ]2 [ ]8 Decimal a binario, de binario a octal Ejem. Convertir el número 15310 a base ()8 15310 [ 010 011 001 ]2 2318 (en la lamina 7 podrá visualizar esta relación) Nota: La conversión de binario a octal se explicara con más detalle cuando se vea el sistema binario

Conversión de decimal a Octal Segundo Método. De las divisiones sucesivas, consiste en dividir el número decimal entre 8 hasta que el cociente sea igual a cero. Convertir 7565810 a ? 8 75658 9457 1182 147 18 2 2 0 8 2 1 6 3 2 2 7565810 = 2236128 Convertir 634810 a ? 8 6348 793 99 12 1 1 0 8 4 1 3 4 1 7565810 = 143148

Conversión de decimal a Hexadecimal Primer Método. Consiste en convertir el numero en base 10 a base 2 y luego de base 2 a base 16 [ ]10 [ ]2 [ ]16 Decimal a binario, de binario a hexadecimal Ejm. Convertir el número 15310 a base ()16 15310 [ 0 1001 ]2 9916 (en la lamina 7 podrá visualizar esta relación) Nota: La conversión de binario a hexadecimal se explicara con más detalle cuando se vea el sistema hexadecimal

Conversión de decimal a Hexadecimal Segundo Método. Consiste en realizar divisiones sucesivas pero dividiendo entre 16 Convertir 1037910 a ? 16 10379 648 40 2 0 16 11 B 8 8 2 1037910 = 288 B 16

Sistema Binario El sistema de numeración binario utiliza sólo dos dígitos, el cero (0) y el uno (1). En una cifra binaria, cada dígito tiene distinto valor dependiendo de la posición que ocupe. El valor de cada posición es el de una potencia de base 2, elevada a un exponente igual a la posición del dígito menos uno. Se puede observar que, tal y como ocurría con el sistema decimal, la base de la potencia coincide con la cantidad de dígitos utilizados (2) para representar los números. Representar el número (1010)2 en forma posicional. Tiene cuatro dígitos enteros p=4 y 0 dígitos fraccionarios. (1010)2 = di 2 i + d j 2 –(i = d 02 0 + d 12 1 + d 22 2 + d 32 3 + d = 0 x 1 + 1 x 2 + 0 x 4 + 1 x 8 (1010)2 = (10)10 42 4

Conversión de binario a decimal, ejemplo: Convertir el número (11011) a decimal 110112 = 1 x 24 + 1 x 23 + 0 x 22 + 1 x 21 + 1 x 20 = 16 + 8 + 0 + 2 + 1 110112 = 2710

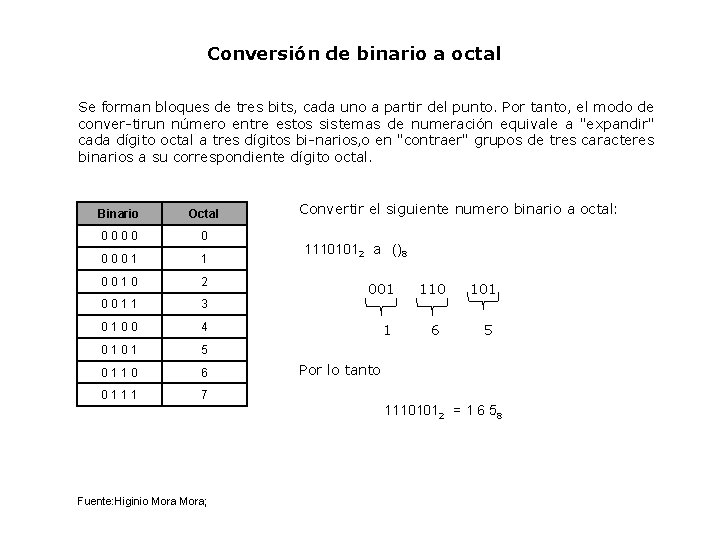
Conversión de binario a octal Se forman bloques de tres bits, cada uno a partir del punto. Por tanto, el modo de conver tir un número entre estos sistemas de numeración equivale a "expandir" cada dígito octal a tres dígitos bi narios, o en "contraer" grupos de tres caracteres binarios a su correspondiente dígito octal. Binario Octal 0000 0 0001 1 0010 2 0011 3 0100 4 0101 5 0110 6 0111 7 Convertir el siguiente numero binario a octal: 11101012 a ()8 001 110 101 1 6 5 Por lo tanto 11101012 = 1 6 58 Fuente: Higinio Mora;

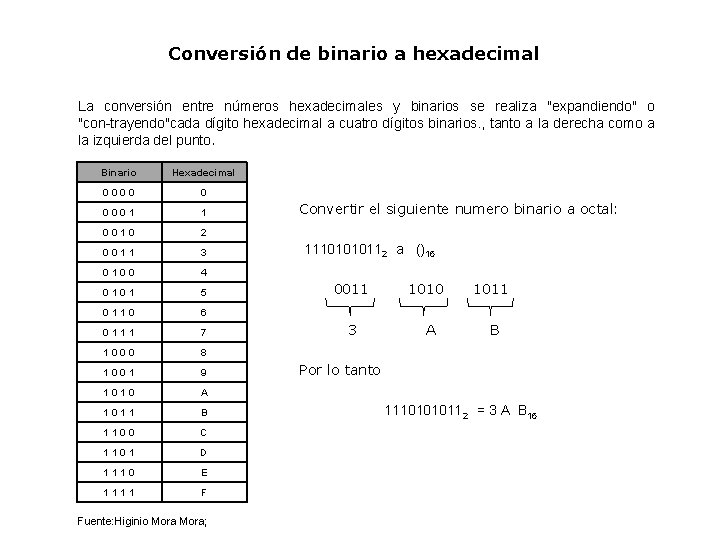
Conversión de binario a hexadecimal La conversión entre números hexadecimales y binarios se realiza "expandiendo" o "con trayendo"cada dígito hexadecimal a cuatro dígitos binarios. , tanto a la derecha como a la izquierda del punto. Binario Hexadecimal 0000 0 0001 1 0010 2 0011 3 0100 4 0101 5 0110 6 0111 7 1000 8 1001 9 1010 A 1011 B 1100 C 1101 D 1110 E 1111 F Fuente: Higinio Mora; Convertir el siguiente numero binario a octal: 11101010112 a ()16 0011 1010 1011 3 A B Por lo tanto 11101010112 = 3 A B 16

Sistema Octal En el sistema de numeración octal, los números se representan mediante ocho dígitos diferentes: 0, 1, 2, 3, 4, 5, 6 y 7. Cada dígito tiene, naturalmente, un valor distinto dependiendo del lu gar que ocupen. El valor de cada una de las posiciones viene determinado por las potencias de base 8. Correspondencia con el binario: 8 = 23 Una cifra en octal corresponde a 3 binarias Ejemplos: 10001101100. 110102 = 2154. 648 (Binario a Octal) 537. 248 = 101011111. 0101002 (Octal a Binario) Conversión Decimal – Octal 760. 3310 1370. 25078 Fuente: Higinio Mora;

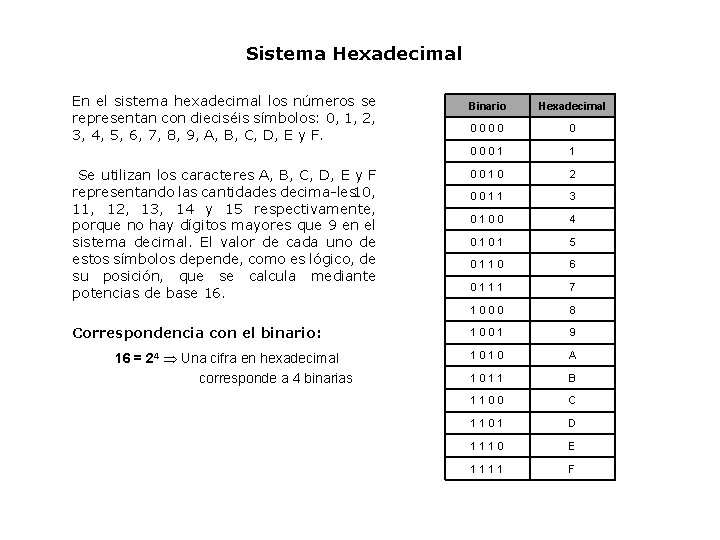
Sistema Hexadecimal En el sistema hexadecimal los números se representan con dieciséis símbolos: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E y F. Se utilizan los caracteres A, B, C, D, E y F representando las cantidades decima les 10, 11, 12, 13, 14 y 15 respectivamente, porque no hay dígitos mayores que 9 en el sistema decimal. El valor de cada uno de estos símbolos depende, como es lógico, de su posición, que se calcula mediante potencias de base 16. Correspondencia con el binario: 16 = 24 Una cifra en hexadecimal corresponde a 4 binarias Binario Hexadecimal 0000 0 0001 1 0010 2 0011 3 0100 4 0101 5 0110 6 0111 7 1000 8 1001 9 1010 A 1011 B 1100 C 1101 D 1110 E 1111 F

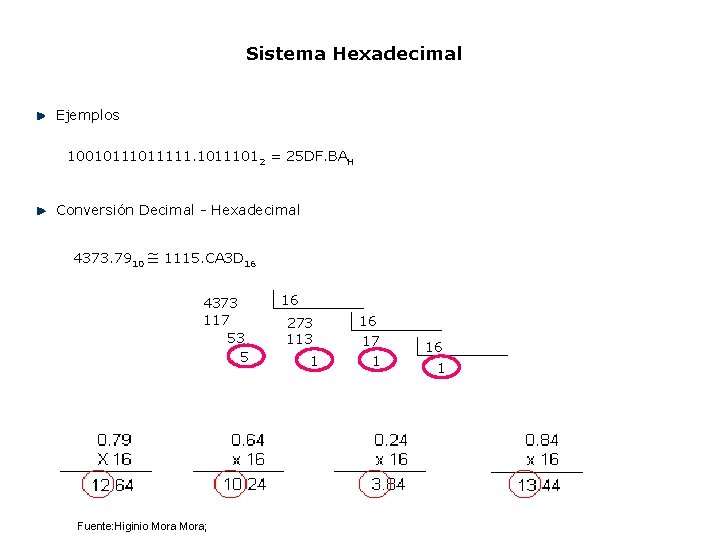
Sistema Hexadecimal Ejemplos 1001011111. 10111012 = 25 DF. BAH Conversión Decimal Hexadecimal 4373. 7910 1115. CA 3 D 16 4373 117 53 5 Fuente: Higinio Mora; 16 273 113 1 16 17 1 16 1

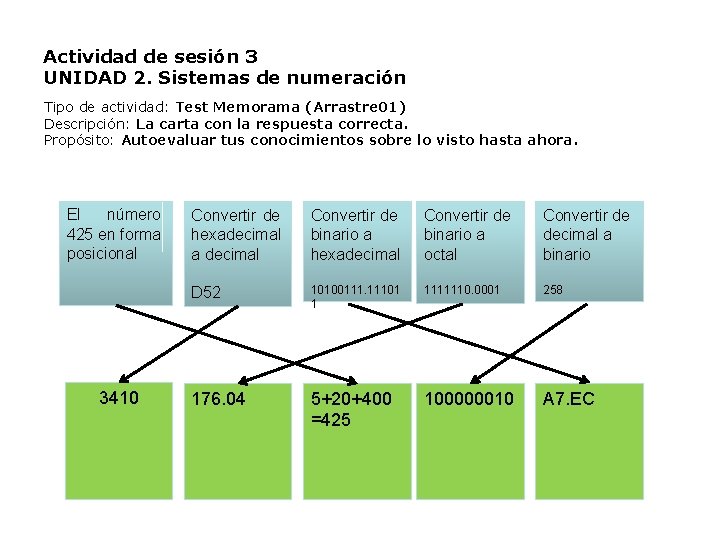
Actividad de sesión 3 UNIDAD 2. Sistemas de numeración Tipo de actividad: Test Memorama (Arrastre 01) Descripción: La carta con la respuesta correcta. Propósito: Autoevaluar tus conocimientos sobre lo visto hasta ahora. El número 425 en forma posicional 3410 Convertir de hexadecimal a decimal Convertir de binario a hexadecimal Convertir de binario a octal Convertir de decimal a binario D 52 10100111. 11101 1 1111110. 0001 258 176. 04 5+20+400 =425 100000010 A 7. EC

Conclusiones En este momento eres capaz comprender lo que es un microprocesador y reconocer los elementos que lo integran Ingresa al link http: //books. google. com/books? id=bm. Lu. H 0 Cs. Ih 0 C&printsec=frontcover&dq=sistemas+ digitales+tocci&hl=es&ei=d 9 j. JTdi. PBKTUi. AK_8 t 2 i. BQ&sa=X&oi=book_result&ct=result&res num=1&ved=0 CCk. Q 6 AEw. AA#v=onepage&q&f=false y ejercita, estudia el primer capitulo para reafirmar tus conocimientos. Ingresa al link http: //www. luventicus. org/articulos/02 A 035/index. html

Lo que veremos en la sesión próxima. • En la siguiente sesión conoceremos aritmética binaria

GLOSARIO sistemas posicionales. se caracterizan porque un símbo lo tiene distinto valor según la posición que ocupa en la cifra. Bit: 0 ó 1

Referencias de Consulta Tocci, Ronald J y Widmer Neals. Sistemas Digitales, Octava Edición. Ed. Pearson Educación. Mexico 2003 DE MIGUEL, Miguel, Arquitectura de computadoras, Teoría y ejercicios resueltos, España, Alfa omega Rama, 2002.

¡Enhorabuena! • Has concluido la Sesión 3 de la Asignatura Arquitectura de Computadoras, correspondiente al Cuarto Cuatrimestre. • Continúa incrementando tus conocimientos, revisa tu siguiente sesión programada.