ObjectOriented Knowledge Representation Jacques Robin Ontologies Reasoning Components

Object-Oriented Knowledge Representation Jacques Robin Ontologies Reasoning Components Agents Simulations

Outline E Object-oriented languages E Review: key concepts of objectorientation E History of OO languages E Motivation for OO software engineering and knowledge representation E First generation OOKR languages E Semantic networks x Classical First-Order Logic (CFOL) E Frames x Semantic Networks E Frames x CFOL E UML E The variety of UML diagrams E Class diagrams E Object diagrams E Meta-knowledge representation and MOF E The UML meta-model E Activity diagrams E UML x Semantic networks E UML x Frames E Limitations of UML Diagrams

Review of Key Object-Orientation Concepts E Class (or concept, or category): abstract representation of a set of individuals with common structural and/or behavioral properties E A class defines a complex type E Object (or individual, or instance): individual instance of a given class E An object conforms to the complex type defined by its class E An object is created by instantiating its class (constructor method) E Each object has a unique identifier (oid) that distinguishes it from other instances of the same class sharing the same properties E The structural properties of a class are a set of attributes (also called fields or slots), which value is constrained to be of a certain subset of types (primitive types or classes) E The structural properties of an object are specific values for these attributes within the ranges defined by its class E The behavioral properties of a class are a set of operations (also called methods, procedures, deamons or functions) that its instances can execute E The signature of a class is the set of type constraints on its attributes and on the parameters and return value of its operations E The properties of a class have various visibilities such as public, protected and private allowing their encapsulation E Classes are organized in a generalization (specialization) hierarchy E Properties are inherited down the hierarchy from a class to its subclasses and its objects

Inheritance E Allows concise knowledge representation through reuse of specifications and implementations among classes and objects down a specialization hierarchy E Types of inheritance: E Structural inheritance E Attribute signature inheritance (constraint inheritance) E Value inheritance E Behavioral inheritance E Operation signature inheritance (constraint inheritance) E Operation code inheritance E Inheritance multiplicity E Simple inheritance (each class restricted to having a single super-class, and each object restricted to belong to a single class) E Multiple inheritance of different properties from different sources E Multiple inheritance of same property from different sources E Inheritance monotonicity E Monotonic inheritance: simple without overriding E Non-monotonic inheritance: with overriding, logically equivalent to default reasoning, semantics beyond Classicial First-Order Logic

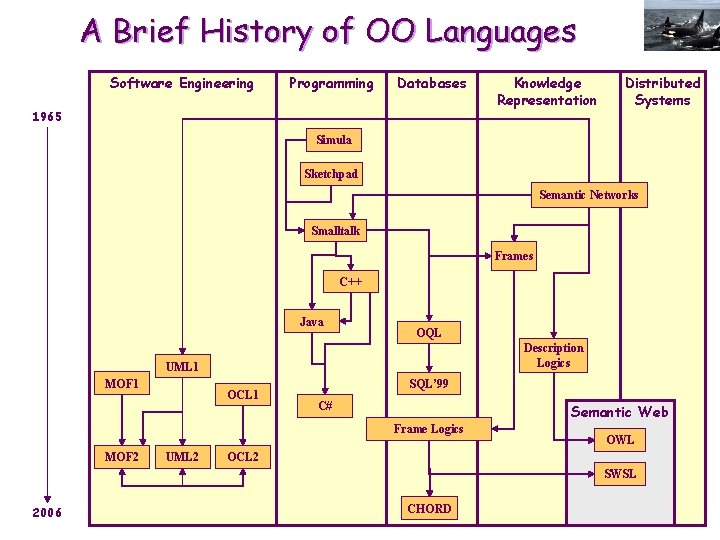
A Brief History of OO Languages Software Engineering Programming Databases 1965 Knowledge Representation Distributed Systems Simula Sketchpad Semantic Networks Smalltalk Frames C++ Java OQL Description Logics UML 1 MOF 1 OCL 1 SQL’ 99 C# Semantic Web Frame Logics MOF 2 UML 2 OWL OCL 2 SWSL 2006 CHORD

Motivation for OO in Software Engineering E Improved productivity, quality, legibility and maintainability in developing software artifacts E Software reuse instead of rewriting or cut and paste E More intuitive E Divide software in abstract entities and relations that directly match common cognitive abstraction of modeled domain E Easy to learn E Unifying notation E Single representation paradigm for all software process stages E Single, unified modeling language (UML)

Initial Motivation for OO in Knowledge Representation E Reasoning at the level of categories E Inheritance as reasoning task E Representing structural knowledge with a notation that is more intuitive than formal logic E Easier to acquire, understand, maintain, etc. E Reasoning about classifying instances into categories and inheritance can internally reuse a logic-based theorem prover, but in a way that is transparent, hidden from the domain expert E Benefits of software engineering carrying over to knowledge (base) engineering

Categories E The organization of objects in categories is a vital part of knowledge representation E Most human reasoning occurs at the abstract level of general categories (intentional knowledge), rather than at the level of individual objects (extensional knowledge) E Partial information: E coming for example from the sensors of an agent, E about an object can be sufficient to classify it into a set of fixed categories E about which general knowledge has been formalized E The missing information: E needed for example for an agent to make a decision about how to handle the object or predict its behavior E about the object can then be derived from the properties of the category E Complex taxomonies involving generalization and composition relationships among categories form a rich network of abstract knowlege onto which to base the reasoning of an agent

Properties of Categories E Disjointness E No common elements E Ex. : male and female E Exhaustive decomposition E Covers the entire set of entities in the represented domain E Ex. : an animal that is not male, must be female E Partition E Exhaustive decomposition into disjoint categories E Counter-example: citizenships E Composition E A category of objects has another category of objects as one of its constituing parts E Ex. : A state is part of federal nation, a chapter is part of a book

Semantic Networks E Category-oriented knowledge visual modeling E Each category and instance is represented by a network node E Each relationship between categories and instances is represented by a network link E Special subset. Of and part. Of relationships among categories E Special member. Of relationship between a category and its instances E Early semantic networks had single isa relationship that did not distinguish between subset. Of and member. Of E Efficient algorithms to derive instance properties from their category: E By value inheritance E By link path query

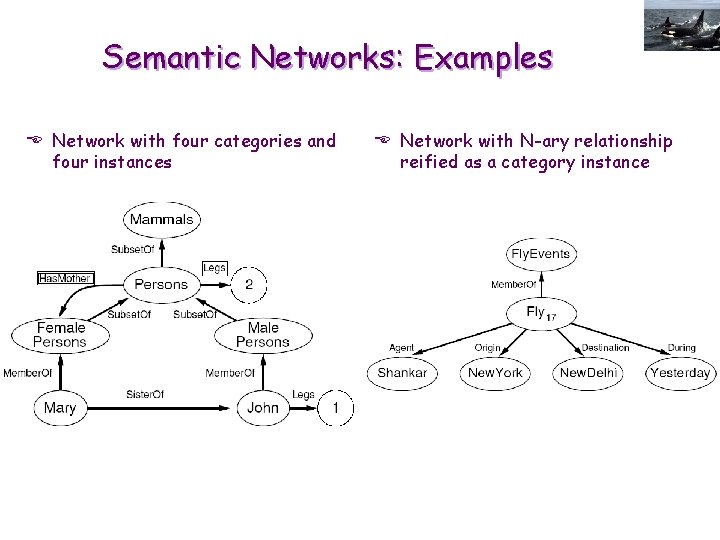
Semantic Networks: Examples E Network with four categories and four instances E Network with N-ary relationship reified as a category instance

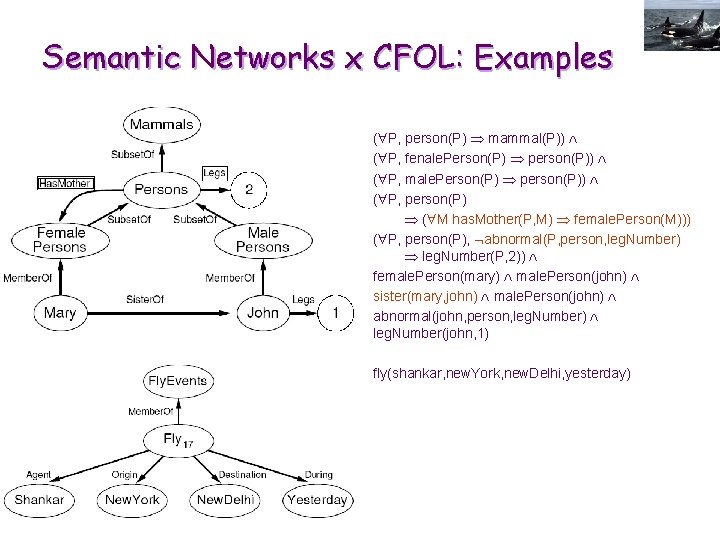
Semantic Networks x CFOL: Examples ( P, person(P) mammal(P)) ( P, fenale. Person(P) person(P)) ( P, male. Person(P) person(P)) ( P, person(P) ( M has. Mother(P, M) female. Person(M))) ( P, person(P), abnormal(P, person, leg. Number) leg. Number(P, 2)) female. Person(mary) male. Person(john) sister(mary, john) male. Person(john) abnormal(john, person, leg. Number) leg. Number(john, 1) fly(shankar, new. York, new. Delhi, yesterday)

Early Semantic Networks E Shortcut the formalization level of knowledge representation E Directly mapped the graphical, knowledge level to the user-hidden programming code, implementation level E Inference engines implemented reasoning that was unsound with semantic networks defined by most users, due to lack of: E Well-defined semantics for non-monotonic inheritance and reification of N-ary relationships as categories E Distinction between categories and instances

Late Semantic Networks E Incorporated ever increasing types of links to get back expressive power close to that of CFOL E Lost visual modeling simplicity and intuitiveness E Remaining limitations: E Inheritance and link navigation sole inference services E No construct to represent behavioral knowledge, state changes, events and time E Currently obsolete, superseded by Description Logics E Most recent DL engines use CFOL theorem proving techniques instead of graph traversal techniques to reason correctly and efficiently

Frames E A frame has a name as its identification and describes a complex category or instance using a set of attributes (called slots) E A frame system is a hierarchical organized set of frames. E An evolution of semantic networks E They also implement monotonic and non-monotonic inheritance E Nodes are replaced by frames E Edges are replaced by attributes (slots) E Procedures may be attached to the slots of a frame to: E E Represent behavioral knowledge Implement other forms of reasoning than mere inheritance Provide a knowledge acquisition user-interface Provide a reasoning explanation user-interface

Frames E E Categories (classes) and instances (objects) represented by Frames A frame is composed by slots A slot is composed by facets Facets may be: E Value specification (known or by default) E Constraint over value (type, cardinality) E Procedures (triggers for when the slot is acessed, modified or necessary to derive some fact during reasoning) E Frames hierarchically organized with multiple inheritance of slots E Inheritance is complex (without no formal definition) due to the variety of facets and interactions E Reasoning is implemented comgining inheritance and triggers E Frames used for: E Knowledge representation E Inference engine implementation E Knowledge acquisition interface implementation E Reasoning explanation interface implementation E Frames are always an extension of some host programming language (Lisp, C++, Prolog, etc. )

Frames: example Frame: Course in KB University Slot: enrolls Type: Student Cardinality. Min: 2 Cardinality. Max: 30 Slot: taughtby Type: (UNION Grad. Student Professor) Cardinality. Min: 1 Cardinality. Max: 1 Frame: Bas. Course in KB University Is-a: Course Slot: taughtby Type: Professor Frame: Adv. Course in KB University Is-a: Course Slot: enrolls Type: (INTERSECTION Grad. Student (NOT Undergrad)) Cardinality. Max: 20 Frame: Grad. Student in KB University Is-a: Student Slot: degree Default: Bachelor Frame: Professor in KB University Slot: degree Default: Ph. D. Frame: Student in KB University Frame: Undergrad in KB University Is-a: Student

Frames x CFOL: Example Frame: Course in KB University Slot: enrolls Type: Student Cardinality. Min: 2 Cardinality. Max: 30 Slot: taught. By Type: (UNION Grad. Student Professor) Cardinality. Min: 1 Cardinality. Max: 1 Frame: Adv. Course in KB University Is-a: Course Slot: enrolls Type: (INTERSECTION Grad. Student (NOT Undergrad)) Cardinality. Max: 20 Frame: Professor in KB University Slot: degree Default: Ph. D. part. Of(course, kb. University) fsfv(course, enrolls, type, student) fsfv(course, enrolls, min. Card, 2) fsfv(course, enrolls, max. Card, 30) fsfv(course, taught. By, type, course. Taught. By. Type) ((course. Taught. By. Type = grad. Student) (course. Taught. By. Type = professor)) fsfv(course, taught. By, min. Card, 1) fsfv(course, taught. By, max. Card, 1) part. Of(adv. Course, kb. University) isa(adv. Course, course) fsfv(adv. Course, enrolls, type, adv. Course. Enrolls. Type) includes(adv. Course. Enrolls. Type, grad. Student) excludes(adv. Course. Enrolls. Type, undergrad. Student) part. Of(professor, kb. University) fsfv(professor, degree, default, phd)

Frames: limitations E Non-declarative behavior knowledge representation as host programming language code as prevents direct acquisition from domain expert E No formal semantics E No distinction between categories and instances E Ad-hoc implementation of deduction and abduction usually inefficient as compared to logic-based ones E There are no inductive inference engines for frame learning E Lacks key reuse-oriented facilities of modern OO programming languages such as visibility, interfaces, components, etc.

UML as KR Language E Class diagram: E Modern, well-founded version of semantic networks E Activity diagram E Modern, well-founded version of flow charts E Graphical syntax for procedures E Class diagrams + Activity diagrams : E Graphical syntax of expressive power approximately equivalent to that of Frames E Strengths: E Universal standard, well-thought, well-known and well-tooled (CASE) E Facilitates convergence between software and knowledge engineering E Limitations: E Lack of full UML compilers to executable languages E Lack of inference engine to automatically reasoning with knowlege represented only as UML models E No mathematically defined formal semantics yet E Thus: E Only useful at the knowledge level E Need to be used in conjunction with other language(s) that provide the formalization and/or implementation level

UML Class Diagram E Categories represented as classes (nodes) E Classes encapsulates: E Primitive type properties, attributes E Behaviors, operations E Relationships between classes represented as associations (edges) E Special associations for: E Specialization relationship (reciprocal of isa) E part. Of relationship (aggregation and compositions) E E Reified relationships represented as association classes Role names and cardinality constraints on associations Many other logical constraints built-in class diagram syntax Arbitrary logical constraints relating any part of the class diagram using Object Constraint Language (OCL, cf. next lecture)

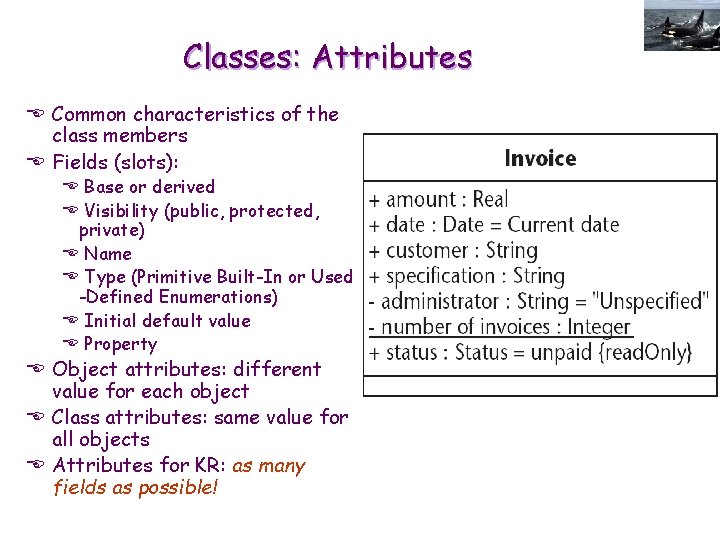
Classes: Attributes E Common characteristics of the class members E Fields (slots): E Base or derived E Visibility (public, protected, private) E Name E Type (Primitive Built-In or Used -Defined Enumerations) E Initial default value E Property E Object attributes: different value for each object E Class attributes: same value for all objects E Attributes for KR: as many fields as possible!

Classes: Operations E Common signature of services provided by the class members E Fields: E Visibility E Name E Input parameter E E E Direction Name Type Multiplicity Default value Property E Return type E Property E Object methods: called on objects E Class methods: called to manipulate class attributes E Operations for KR: as many fields as possible!

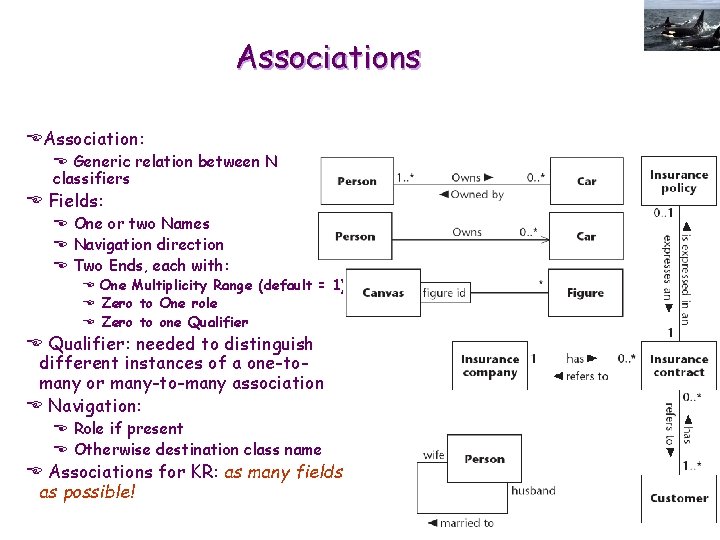
Associations EAssociation: E Generic relation between N classifiers E Fields: E One or two Names E Navigation direction E Two Ends, each with: E One Multiplicity Range (default = 1) E Zero to One role E Zero to one Qualifier E Qualifier: needed to distinguish different instances of a one-tomany or many-to-many association E Navigation: E Role if present E Otherwise destination class name E Associations for KR: as many fields as possible!

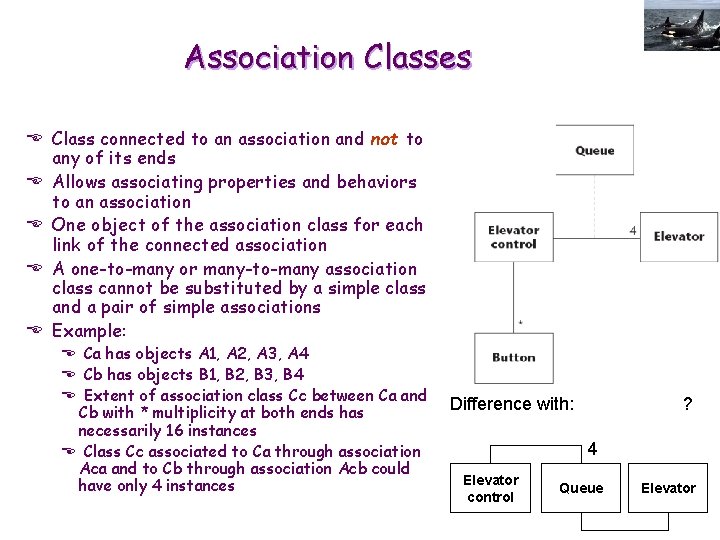
Association Classes E Class connected to an association and not to any of its ends E Allows associating properties and behaviors to an association E One object of the association class for each link of the connected association E A one-to-many or many-to-many association class cannot be substituted by a simple class and a pair of simple associations E Example: E Ca has objects A 1, A 2, A 3, A 4 E Cb has objects B 1, B 2, B 3, B 4 E Extent of association class Cc between Ca and Cb with * multiplicity at both ends has necessarily 16 instances E Class Cc associated to Ca through association Aca and to Cb through association Acb could have only 4 instances Difference with: ? 4 Elevator control Queue Elevator

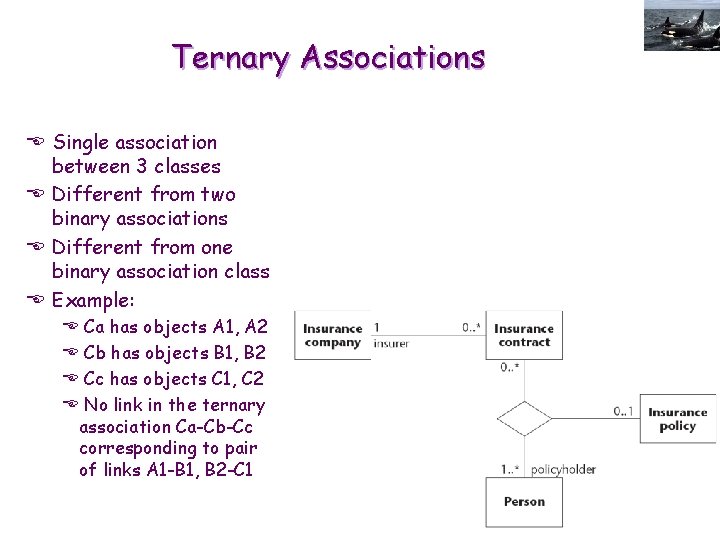
Ternary Associations E Single association between 3 classes E Different from two binary associations E Different from one binary association class E Example: E E Ca has objects A 1, A 2 Cb has objects B 1, B 2 Cc has objects C 1, C 2 No link in the ternary association Ca-Cb-Cc corresponding to pair of links A 1 -B 1, B 2 -C 1

Aggregation Associations E Association with “part-whole” semantics E Associate composite class to its building blocks E Static, definitional characteristic of the “whole” class E In contrast to composite structure diagrams that model dynamic, configuration characteristic of the containing class E Shared aggregation: E Many-to-many aggregation

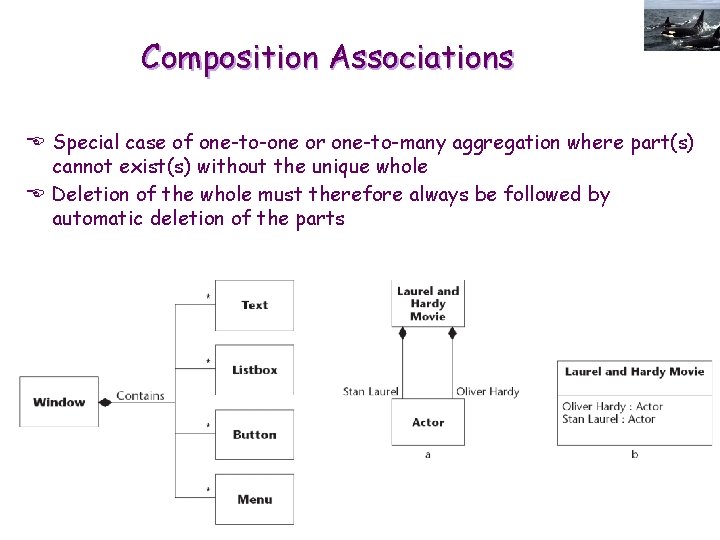
Composition Associations E Special case of one-to-one or one-to-many aggregation where part(s) cannot exist(s) without the unique whole E Deletion of the whole must therefore always be followed by automatic deletion of the parts

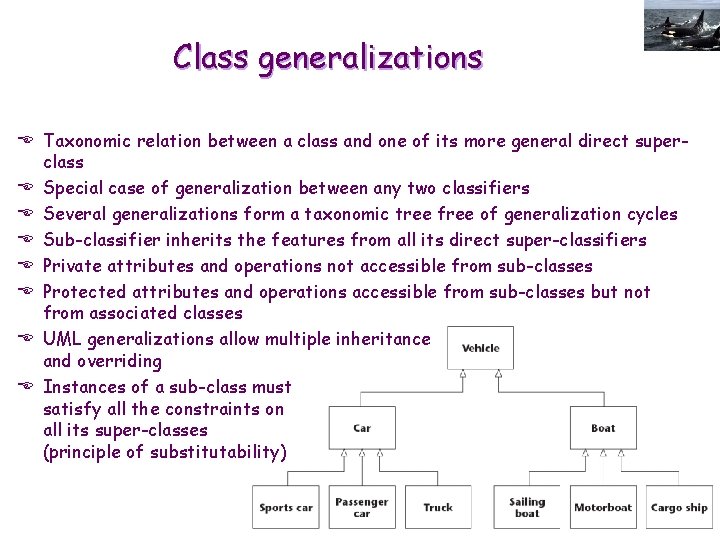
Class generalizations E Taxonomic relation between a class and one of its more general direct superclass E Special case of generalization between any two classifiers E Several generalizations form a taxonomic tree free of generalization cycles E Sub-classifier inherits the features from all its direct super-classifiers E Private attributes and operations not accessible from sub-classes E Protected attributes and operations accessible from sub-classes but not from associated classes E UML generalizations allow multiple inheritance and overriding E Instances of a sub-class must satisfy all the constraints on all its super-classes (principle of substitutability)

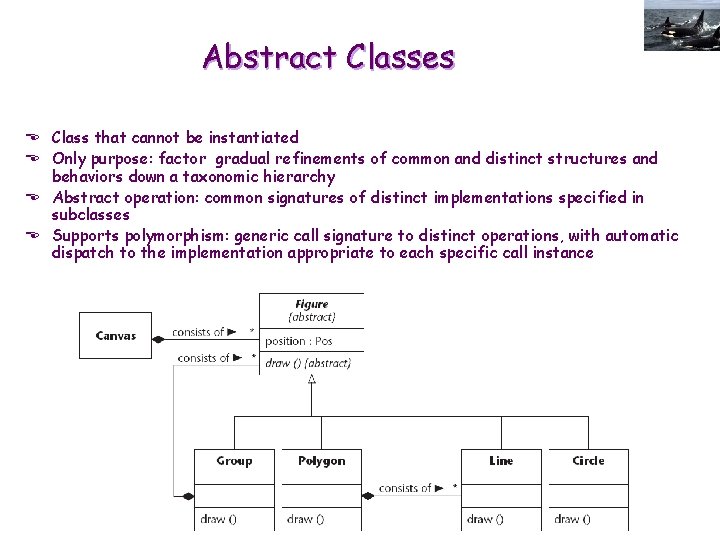
Abstract Classes E Class that cannot be instantiated E Only purpose: factor gradual refinements of common and distinct structures and behaviors down a taxonomic hierarchy E Abstract operation: common signatures of distinct implementations specified in subclasses E Supports polymorphism: generic call signature to distinct operations, with automatic dispatch to the implementation appropriate to each specific call instance

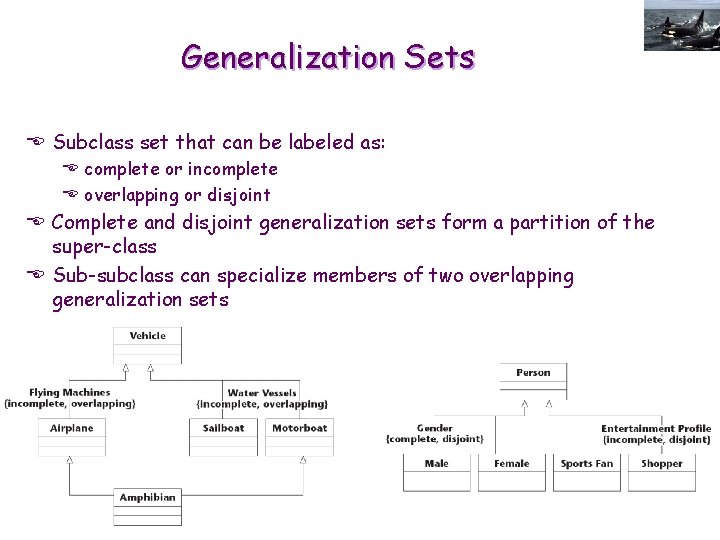
Generalization Sets E Subclass set that can be labeled as: E complete or incomplete E overlapping or disjoint E Complete and disjoint generalization sets form a partition of the super-class E Sub-subclass can specialize members of two overlapping generalization sets

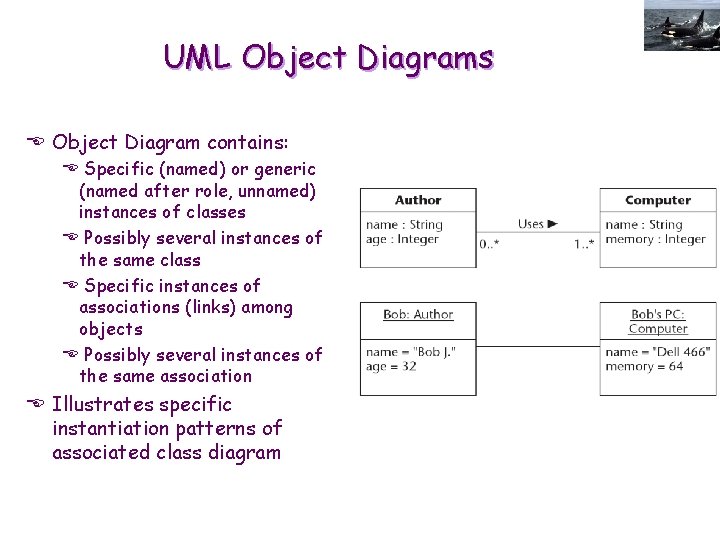
UML Object Diagrams E Object Diagram contains: E Specific (named) or generic (named after role, unnamed) instances of classes E Possibly several instances of the same class E Specific instances of associations (links) among objects E Possibly several instances of the same association E Illustrates specific instantiation patterns of associated class diagram

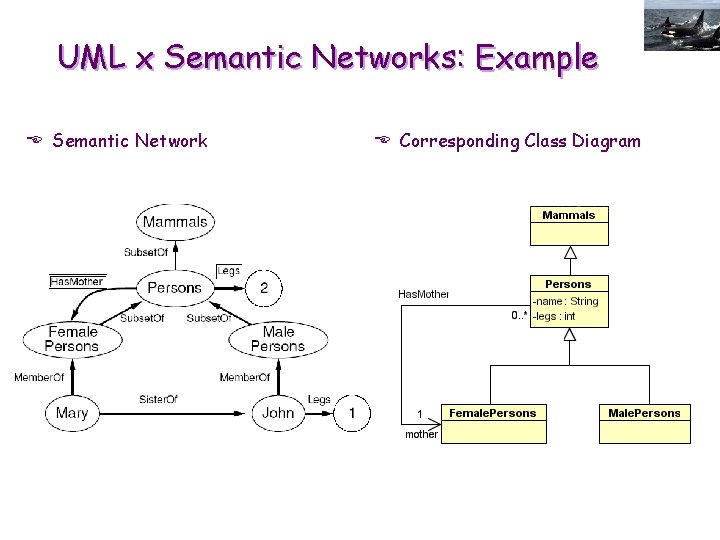
UML x Semantic Networks: Example E Semantic Network E Corresponding Class Diagram

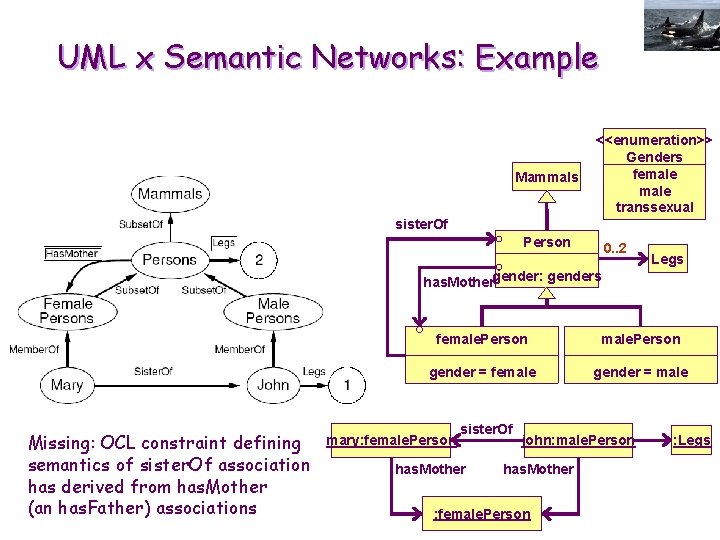
UML x Semantic Networks: Example Mammals <<enumeration>> Genders female transsexual sister. Of Person 0. . 2 Legs has. Mothergender: genders Missing: OCL constraint defining semantics of sister. Of association has derived from has. Mother (an has. Father) associations female. Person gender = female gender = male mary: female. Person sister. Of has. Mother john: male. Person has. Mother : female. Person : Legs

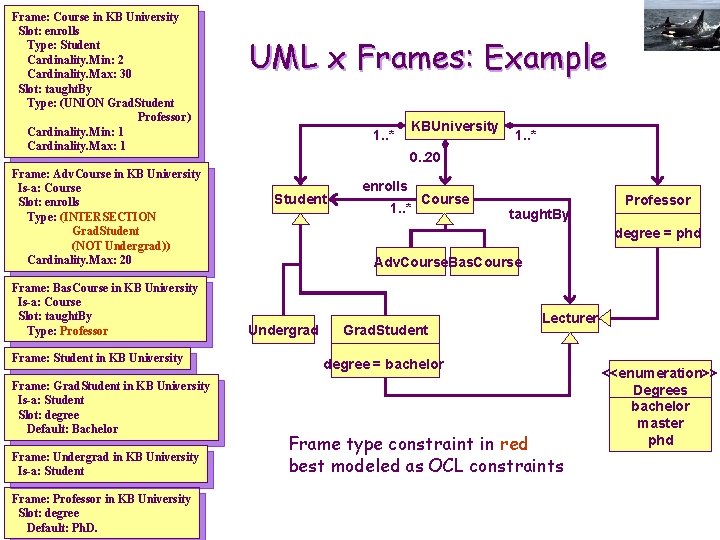
Frame: Course in KB University Slot: enrolls Type: Student Cardinality. Min: 2 Cardinality. Max: 30 Slot: taught. By Type: (UNION Grad. Student Professor) Cardinality. Min: 1 Cardinality. Max: 1 Frame: Adv. Course in KB University Is-a: Course Slot: enrolls Type: (INTERSECTION Grad. Student (NOT Undergrad)) Cardinality. Max: 20 Frame: Bas. Course in KB University Is-a: Course Slot: taught. By Type: Professor Frame: Student in KB University Frame: Grad. Student in KB University Is-a: Student Slot: degree Default: Bachelor Frame: Undergrad in KB University Is-a: Student Frame: Professor in KB University Slot: degree Default: Ph. D. UML x Frames: Example 1. . * KBUniversity 1. . * 0. . 20 Student enrolls 1. . * Course taught. By Professor degree = phd Adv. Course. Bas. Course Undergrad Grad. Student Lecturer degree = bachelor Frame type constraint in red best modeled as OCL constraints <<enumeration>> Degrees bachelor master phd

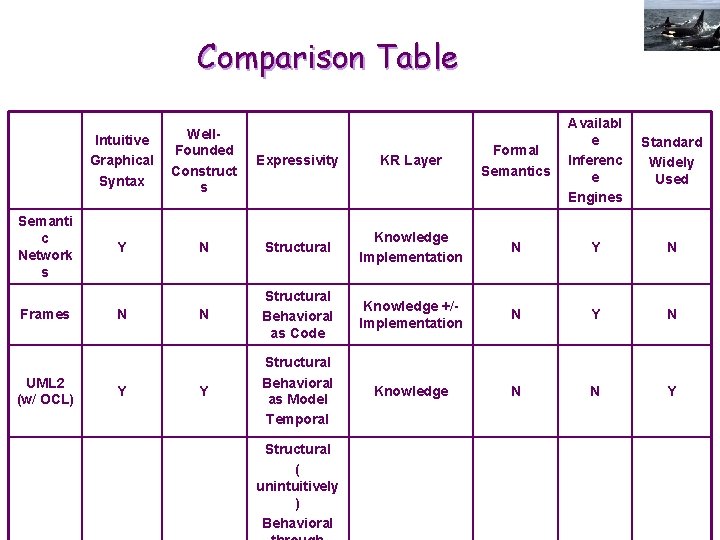
Comparison Table Semanti c Network s Frames UML 2 (w/ OCL) KR Layer Formal Semantics Availabl e Inferenc e Engines Standard Widely Used Structural Knowledge Implementation N Y N N Structural Behavioral as Code Knowledge +/Implementation N Y Structural Behavioral as Model Temporal Knowledge N N Y Intuitive Graphical Syntax Well. Founded Construct s Expressivity Y N N Y Structural ( unintuitively ) Behavioral

Meta-Object Facility (MOF) E Structural meta-knowledge representation language E Reuses UML class diagrams to specify, in an object-oriented way, the abstract syntax of computational languages E Advantages over BNF grammars: Visual clarity Abstract Terminals with internal structure and behaviors Richer variety of relation semantics among non-terminals: specialization, aggregation, composition and simple associations instead of merely linearization order E Reuse through inheritance, package import and package merge E E E A MOF specification of the abstract syntax of a language L is called a meta-model of L

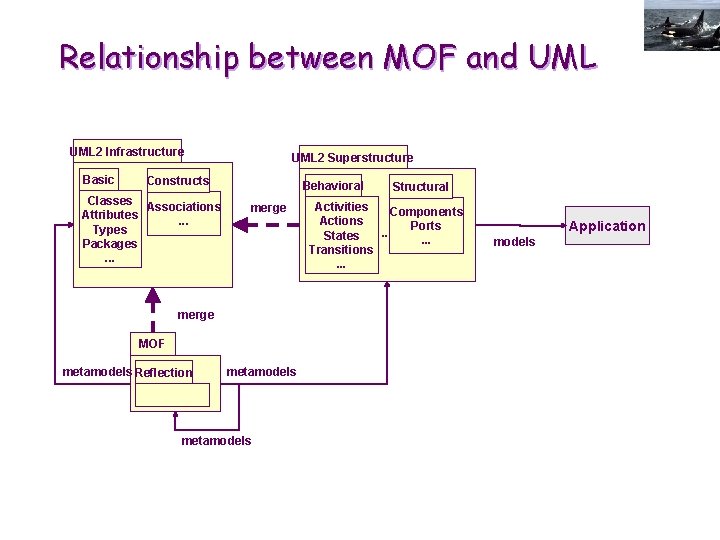
Relationship between MOF and UML 2 Infrastructure Basic UML 2 Superstructure Constructs Classes Associations Attributes. . . Types. . . Packages. . . Behavioral merge MOF metamodels Reflection metamodels . . . metamodels Structural Activities Components Actions Ports. . . States. . . Transitions. . . Application models

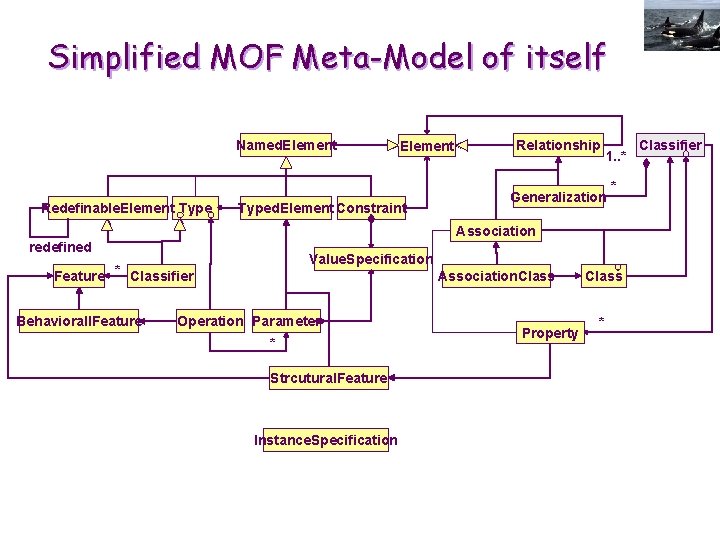
Simplified MOF Meta-Model of itself Named. Element Redefinable. Element Typed. Element Constraint Relationship 1. . * Generalization * Association redefined Value. Specification Feature * Classifier Behaviorall. Feature Association. Class Operation Parameter * Strcutural. Feature Instance. Specification Property Class * Classifier

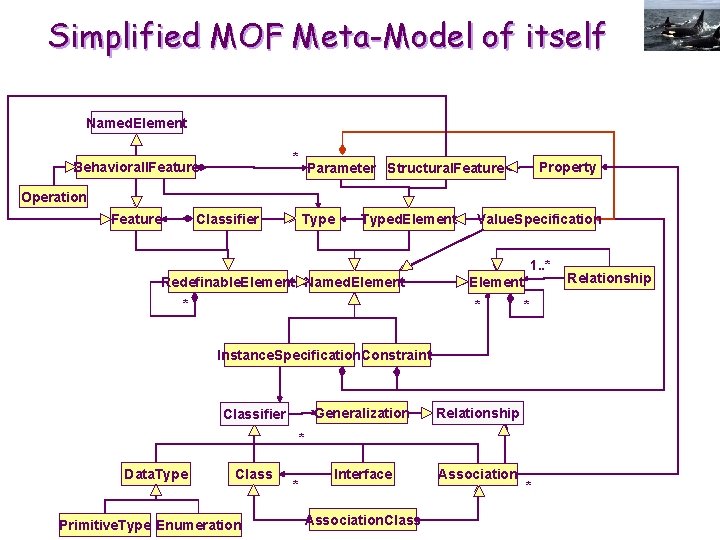
Simplified MOF Meta-Model of itself Named. Element * Behaviorall. Feature Property Parameter Structural. Feature Operation Feature Type Classifier Typed. Element Value. Specification 1. . * Redefinable. Element Named. Element * * Instance. Specification. Constraint Classifier Generalization Relationship Interface Association * Data. Type Class Primitive. Type Enumeration * Association. Class * Relationship

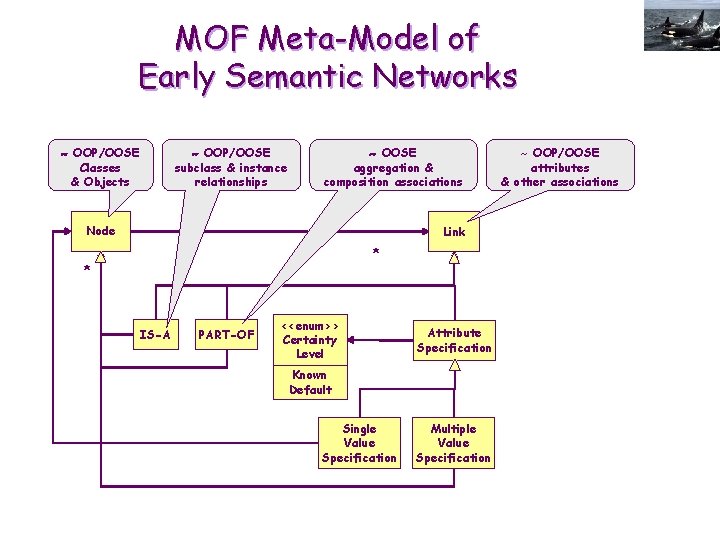
MOF Meta-Model of Early Semantic Networks OOP/OOSE Classes & Objects OOP/OOSE subclass & instance relationships OOSE aggregation & composition associations Node Link * * IS-A PART-OF <<enum>> Certainty Level Attribute Specification Known Default Single Value Specification Multiple Value Specification ~ OOP/OOSE attributes & other associations

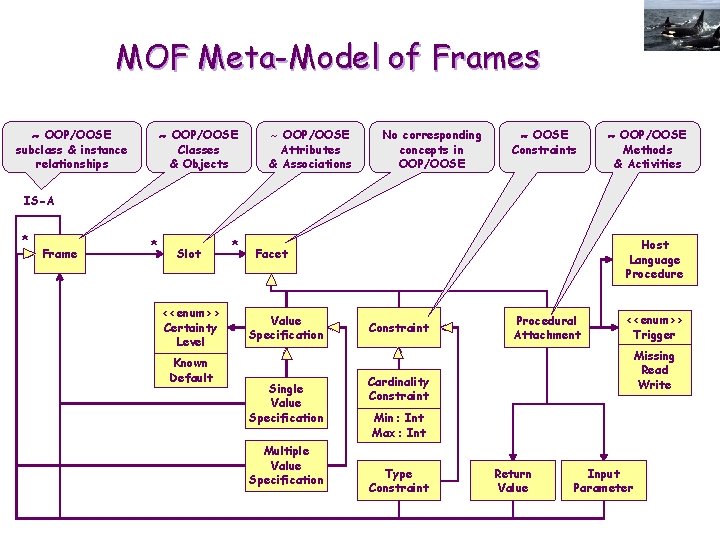
MOF Meta-Model of Frames OOP/OOSE subclass & instance relationships OOP/OOSE Classes & Objects ~ OOP/OOSE Attributes & Associations No corresponding concepts in OOP/OOSE Constraints OOP/OOSE Methods & Activities IS-A * Frame * Slot <<enum>> Certainty Level Known Default * Host Language Procedure Facet Value Specification Single Value Specification Multiple Value Specification Constraint Procedural Attachment <<enum>> Trigger Missing Read Write Cardinality Constraint Min: Int Max: Int Type Constraint Return Value Input Parameter

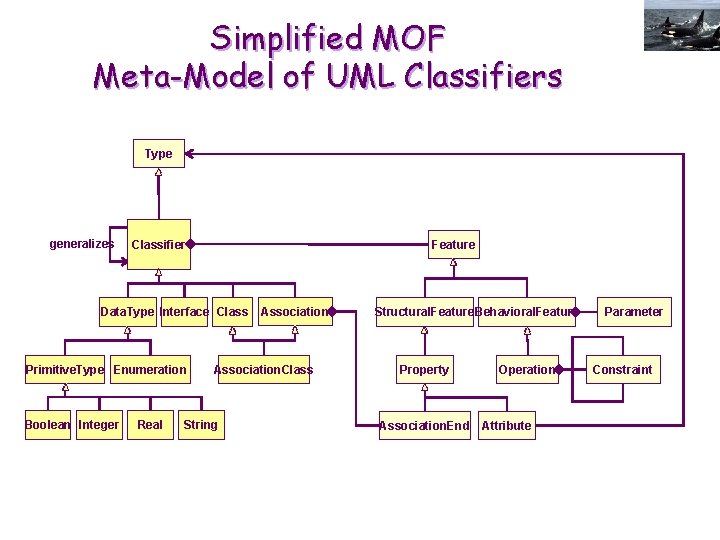
Simplified MOF Meta-Model of UML Classifiers Type generalizes Classifier Feature Data. Type Interface Class Primitive. Type Enumeration Boolean Integer Real Association. Class String Structural. Feature. Behavioral. Feature Property Operation Association. End Attribute Parameter Constraint

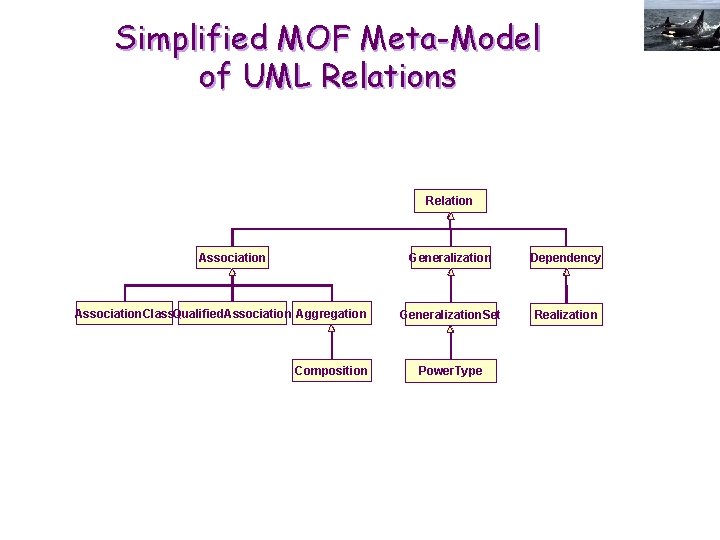
Simplified MOF Meta-Model of UML Relations Relation Association. Class. Qualified. Association Aggregation Composition Generalization Dependency Generalization. Set Realization Power. Type