ObjectOriented Data Structures 1 Objectives To understand classical

Object-Oriented Data Structures 1

Objectives • • To understand classical data structures. To understand limitations of arrays. To implement a list interface using an array. To implement a list interface using a linked list. • To implement a stack using an array. • To implement a queue using a linked list. 2

Data Structures An abstract data structure (interface or abstract data type) contains: method signatures: designed to manipulate data A data structure (implementation) contains: data fields (usually private) method implementations 3

Limitations of arrays • changing the capacity and transferring the data during a run is expensive • insert(), delete(), sort(), search() are expensive 4

Four Classic Data Structures Four classic data structures (think interface): list stack queue binary tree List: sequential data insertion() , deletion() (anywhere in both cases) retrieve(), size(), ismember(), isempty() Stack: sequential data insertion()=push(), deletion()=pop() (both from top) Queue: sequential data insertion()=enqueue(), deletion()=dequeue() (rear and front respectively) Binary tree: data insertion(), deletion() (anywhere in both cases) searching(), sorting() 5

List implementations Array: – dynamically adjusted in size – When full, double size (hidden) and copy elements from old array to new array Linked List: – Consists of nodes that hold data and reference to next node – Keep track of first node and (optionally) last node 6

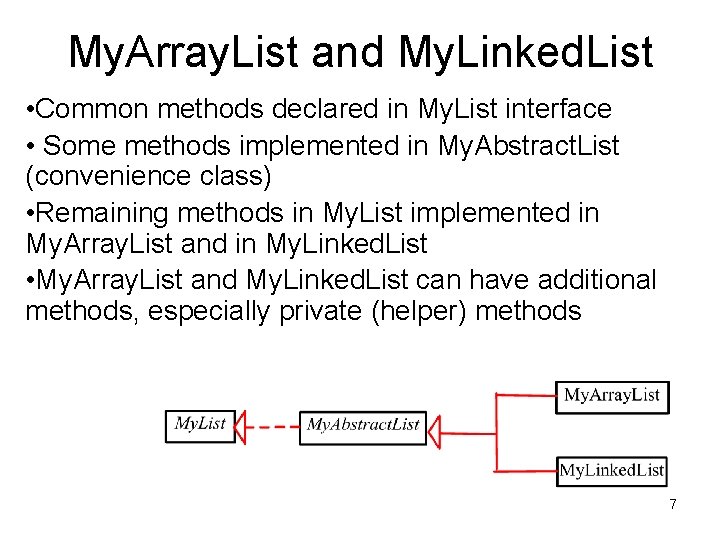
My. Array. List and My. Linked. List • Common methods declared in My. List interface • Some methods implemented in My. Abstract. List (convenience class) • Remaining methods in My. List implemented in My. Array. List and in My. Linked. List • My. Array. List and My. Linked. List can have additional methods, especially private (helper) methods 7

UML: My. List (Interface), My. Abstract. List 8

Array implementation Java. util. Array or My. Array. List • is a fixed-size data structure. – – – Object data[]; Object newdata[]; data= new (Object[10]); Fill data; If (data is full) • Newdata =new (Object[(data. length)*2); • Newdata =data; • Gc() is called automatically for data 9

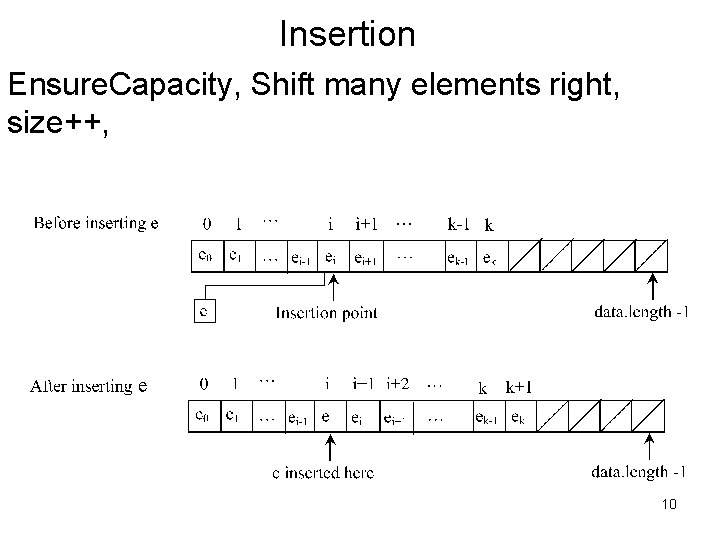
Insertion Ensure. Capacity, Shift many elements right, size++, 10

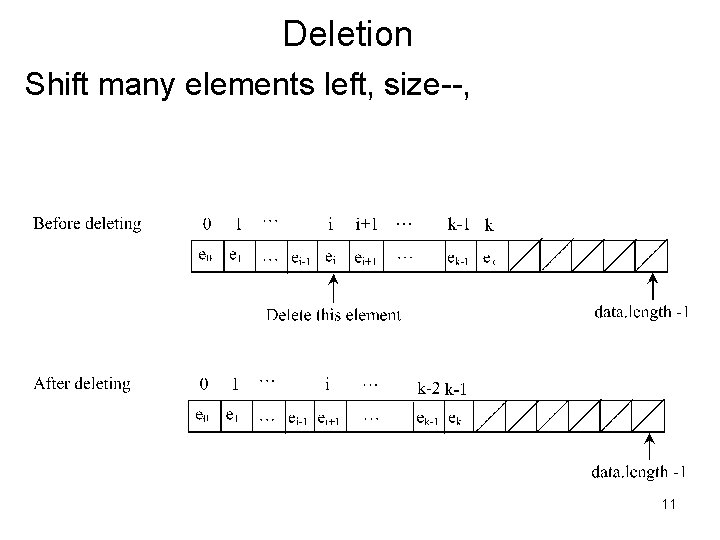
Deletion Shift many elements left, size--, 11

Implementing My. Array. List Test. List Run 12

Add or remove? Use Linked Lists My. Array. List: • get(int index) /*cheap*/ • set(int index, Object o) /*cheap*/ • add(int index, Object o) /*expensive*/ • remove(int index) /*expensive*/ 13

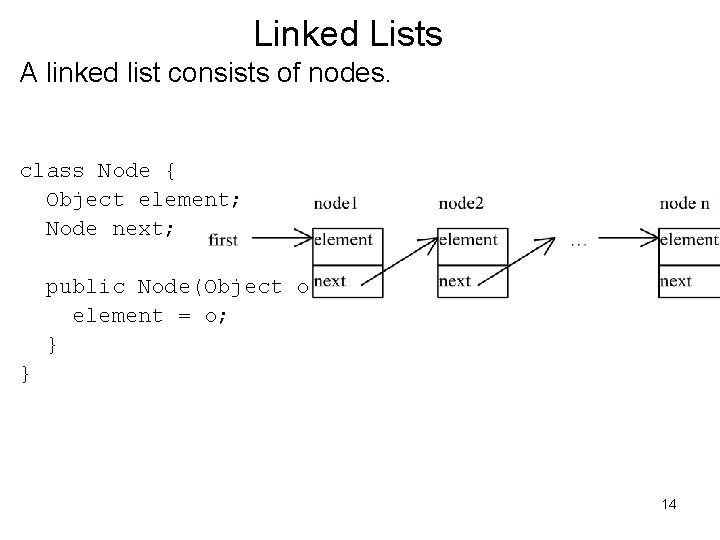
Linked Lists A linked list consists of nodes. class Node { Object element; Node next; public Node(Object o) { element = o; } } 14

Nodes in a Linked List Node first, last; first = new Node(new Circle(1)); last = first; last. next = new Node(new Circle(2)); last = last. next; last. next = new Node(new Circle(3)); last = last. next; 15

My. Linked. List My Linked. List 16

The add. First(Object o) Method size is protected in My. Abstract. List, it can be accessed in My. Linked. List. When a new element is added to the list, size is incremented by 1, and when an element is removed from the list, size is decremented by 1. add. First(Object o) creates a new node to store the element and inserts the node at the beginning of the list. After the insertion, first =new. 17

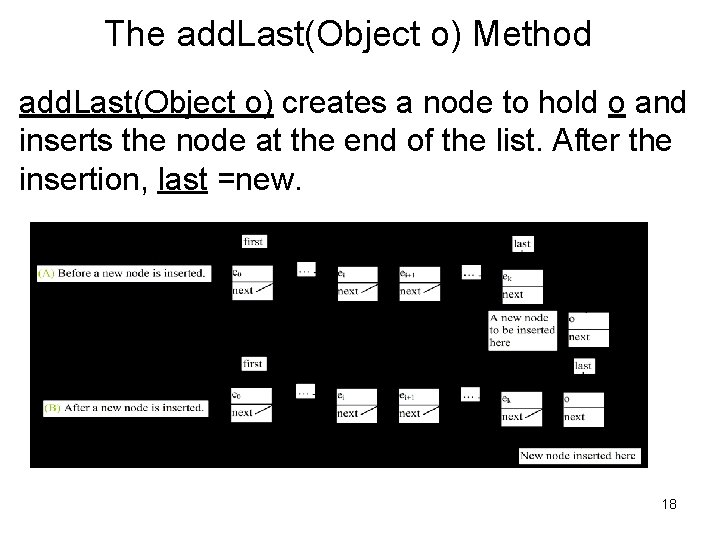
The add. Last(Object o) Method add. Last(Object o) creates a node to hold o and inserts the node at the end of the list. After the insertion, last =new. 18

The add(int index, Object o) Method add(int index, Object o) method adds o to the list at index. Case 1: if (index==0) call add. First(o) Case 2: if (index >=size) call add. Last(o) Case 3: Construct new node to store the new element and locate insertion point with temp and current. The method assigns the new node to current. next and assigns temp to the new node’s next. 19

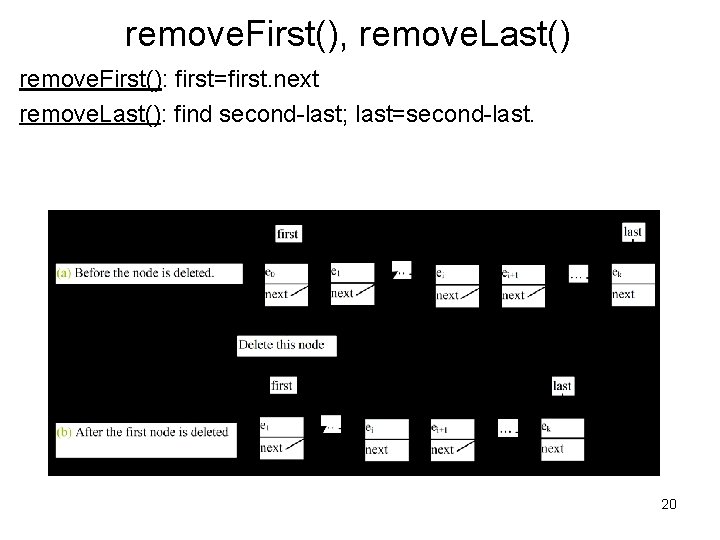
remove. First(), remove. Last() remove. First(): first=first. next remove. Last(): find second-last; last=second-last. 20

Stacks and Queues Special list==Stack • Insert(), delete(), access() only from one end==top • Push(), pop(), peek() • Efficient to use array Special list ==Queue • Insert() at end, delete() at beginning • Enqueue(), dequeue() • Efficient to use linked list 21

Design of Stack and Queue ·Inheritance: Public class Stack extends Array. List Public class Queue extends Linked. List · Composition: Public class Stack { Array. List x; } Public class Queue { Linked. List x } 22

My. Stack and My. Queue My. Stack My. Queue 23