OBJECTIVES To use the To use similarity to

OBJECTIVES: • To use the • To use similarity to find indirect measurements BIG IDEA: Visualization ESSENTIAL UNDERSTANDINGS • Triangles can be shown to be similar based on the relationship of two or three pairs of corresponding parts. • Similar triangles can be used to find unknown measurements MATHEMATICAL PRACTICE • Construct viable arguments and critique the reasoning of others Similar Triangles

Similar Triangles � The definition of similar triangles involves a complicated set of conditions. Postulates and theorems about similarity can provide a shortcut to proving triangles similar. Similar triangles can be used for indirect measurement in a variety of circumstances. Similar triangles are also part of the basic idea of proportionality, which extends through all areas of Geometry. Proving statements in Geometry helps students understand how to develop logical arguments in other areas of their lives. � You can show that two triangles are similar when you know the relationships between only two or three pairs of corresponding parts.

Similarity Postulate and Theorems � Angle-Angle Similarity Postulate: If ________ angles of one triangle are __________ to two angles of another triangle, then the two triangles are __________ � Side-Angle-Side Similarity Theorem: If an ________ of one triangle is __________ to an angle of a second triangle, and the ________ that include the two angles are __________, then the triangles are __________ � Side-Side Similarity Theorem: If the __________ sides of two triangles are __________, then the triangles are __________

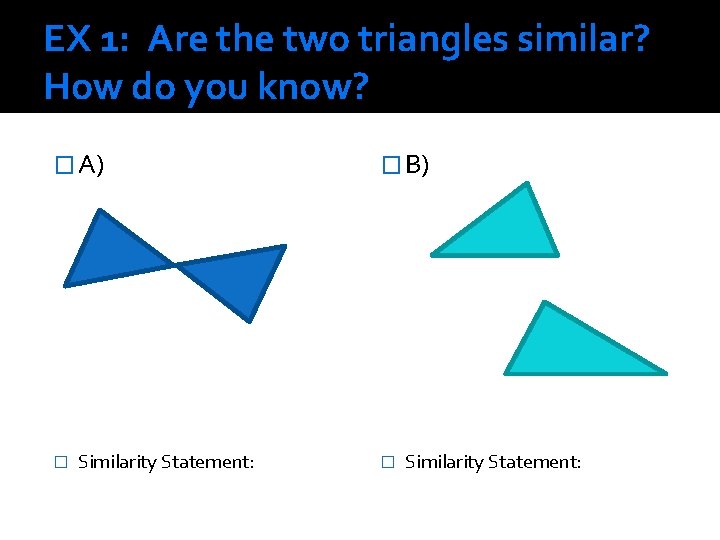
EX 1: Are the two triangles similar? How do you know? � A) � Similarity Statement: � B) � Similarity Statement:

EX 2: Are the two triangles similar? How do you know? � A) � Similarity Statement: � B) � Similarity Statement:

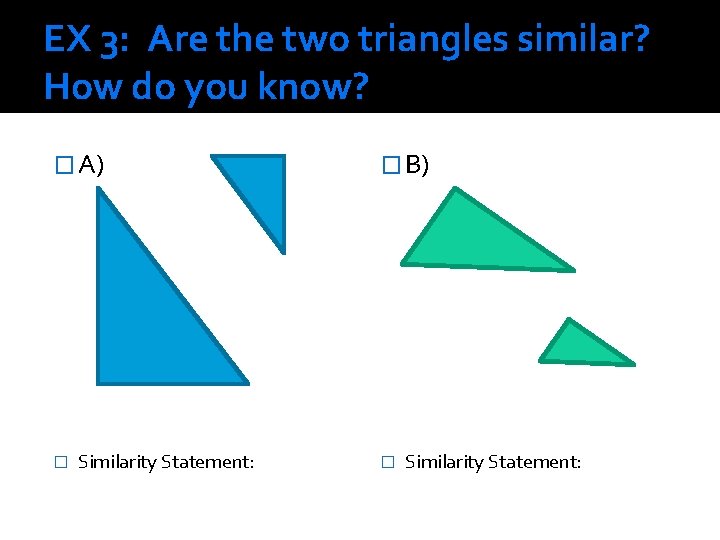
EX 3: Are the two triangles similar? How do you know? � A) � Similarity Statement: � B) � Similarity Statement:

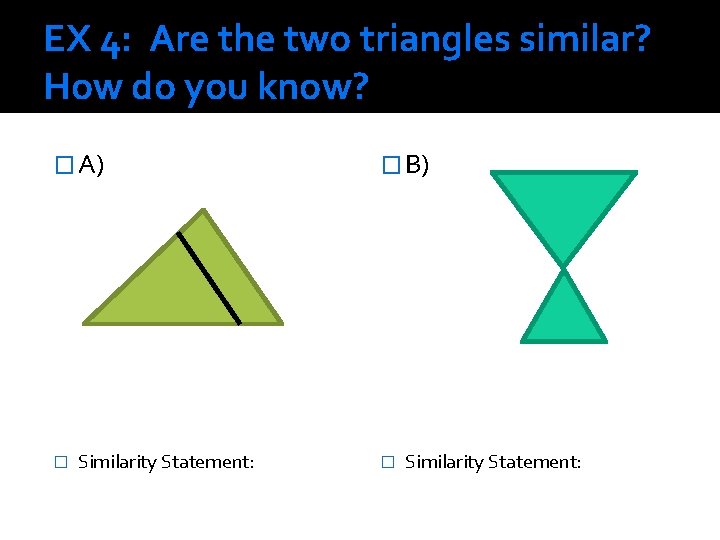
EX 4: Are the two triangles similar? How do you know? � A) � Similarity Statement: � B) � Similarity Statement:

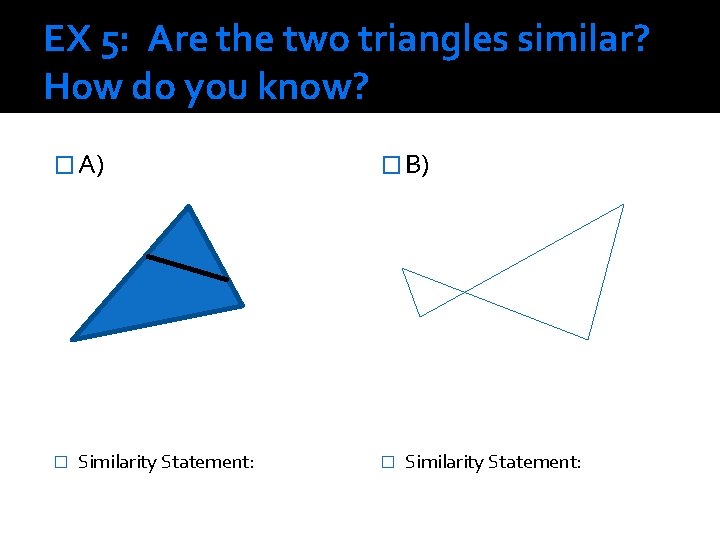
EX 5: Are the two triangles similar? How do you know? � A) � Similarity Statement: � B) � Similarity Statement:

MATH IXL P 7 Mastery Level

Indirect Measurement � Sometimes you can use similar triangles to find lengths that cannot be measured easily using a ruler or other measuring devices. � You can use indirect measurement to find lengths that are difficult to measure directly.

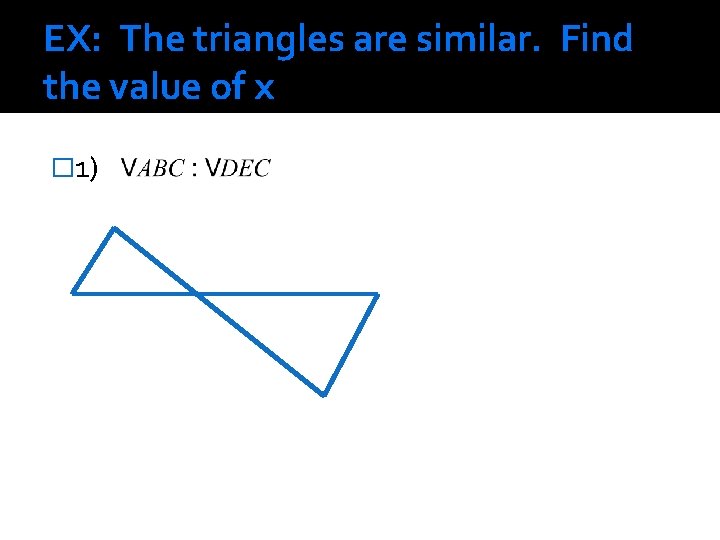
EX: The triangles are similar. Find the value of x � 1)

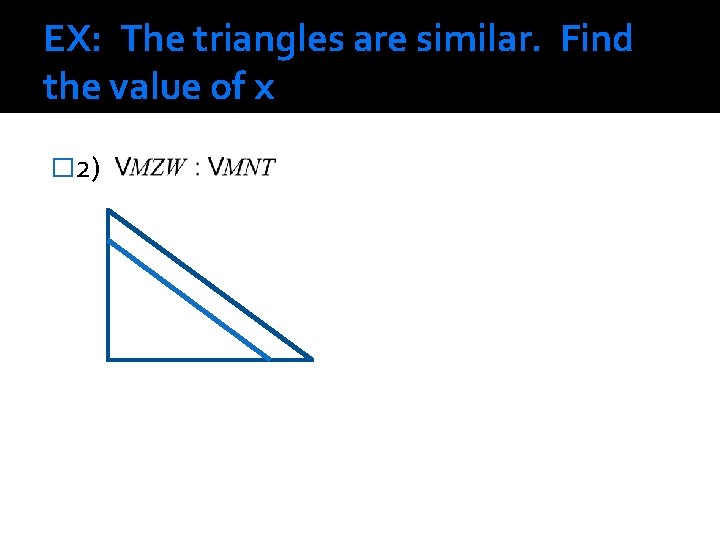
EX: The triangles are similar. Find the value of x � 2)

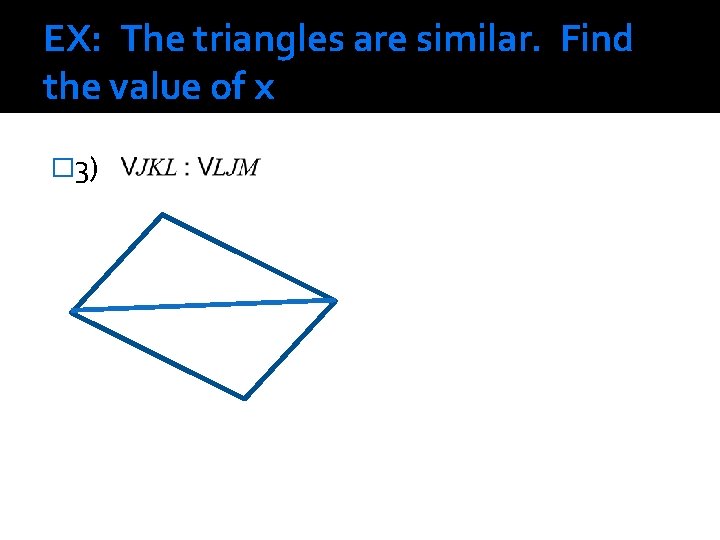
EX: The triangles are similar. Find the value of x � 3)

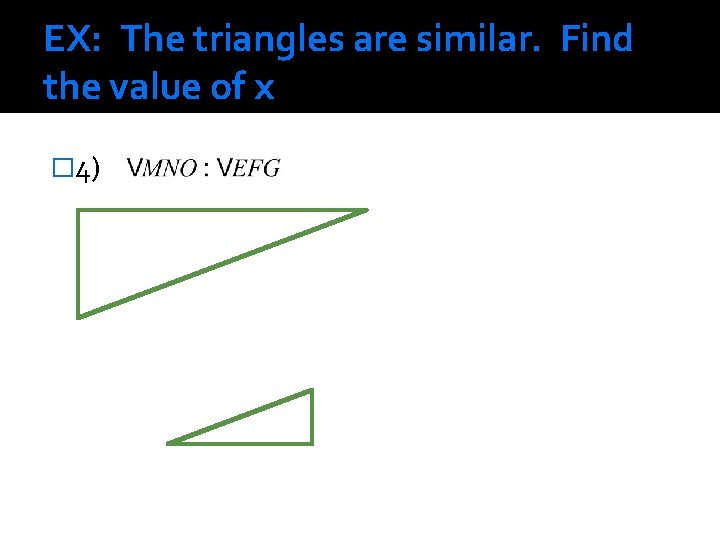
EX: The triangles are similar. Find the value of x � 4)

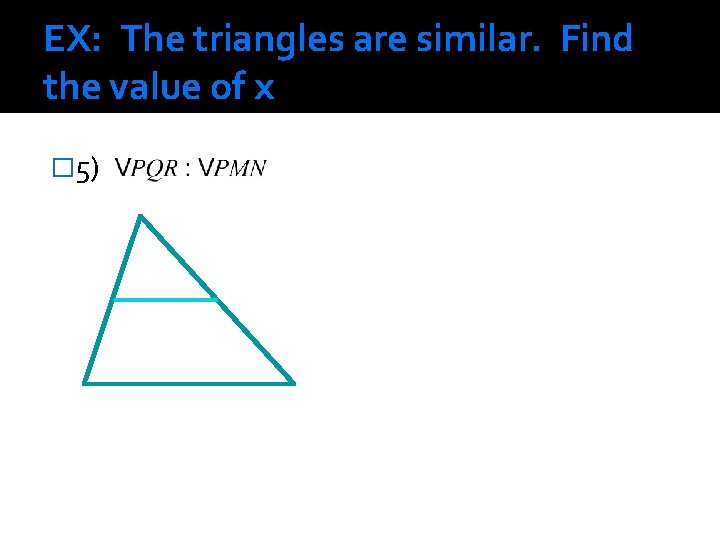
EX: The triangles are similar. Find the value of x � 5)

MATH IXL P 5 Mastery Level