Objectives To determine the degree of polynomial graphs

Objectives: • To determine the degree of polynomial graphs and their turning points. • To identify the leading coefficient of polynomial graphs. • To find zeros of polynomial functions. • To determine the equation of a polynomial from its roots.

Focus o By the end of class, you will need to: o. Create a polynomial graph with a negative leading coefficient and at least 2 real and 2 imaginary roots.

A polynomial function is a function of the form f (x) = ann n n x + an – 1 x n – 1 +· · ·+ a 1 x + aa 00 Where an 0 and the exponents are all whole numbers. For this polynomial function, ann is the leading coefficient, aa 00 is the constant term, and n is the degree. a 0 is the y-intercept. A polynomial function is in standard form if its terms are written in descending order.
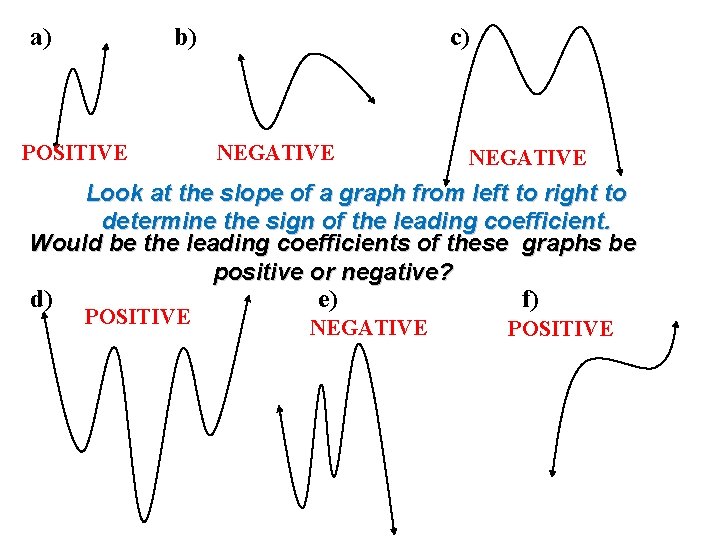
a) b) POSITIVE c) NEGATIVE Look at the slope of a graph from left to right to determine the sign of the leading coefficient. Would be the leading coefficients of these graphs be positive or negative? d) POSITIVE e) NEGATIVE f) POSITIVE

Focus o By the end of class, you will need to: o. Create a polynomial graph with a negative leading coefficient and at least 2 real and 2 imaginary roots.

Four terms to know: ØRoot ØZero ØSolution ØX-intercept They all refer to the same thing!
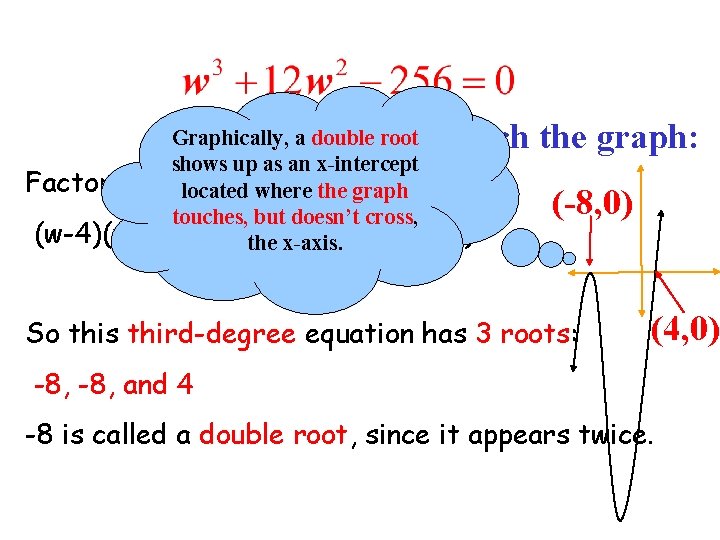
Graphically, a double root shows up as an x-intercept Factored form: located where the graph touches, but doesn’t cross, 2 (w-4)(w+8) =0 the x-axis. (trust Sketch the graph: me) (-8, 0) So this third-degree equation has 3 roots: (4, 0) -8, and 4 -8 is called a double root, since it appears twice.

What is the quadratic function that has roots 4 and -3?
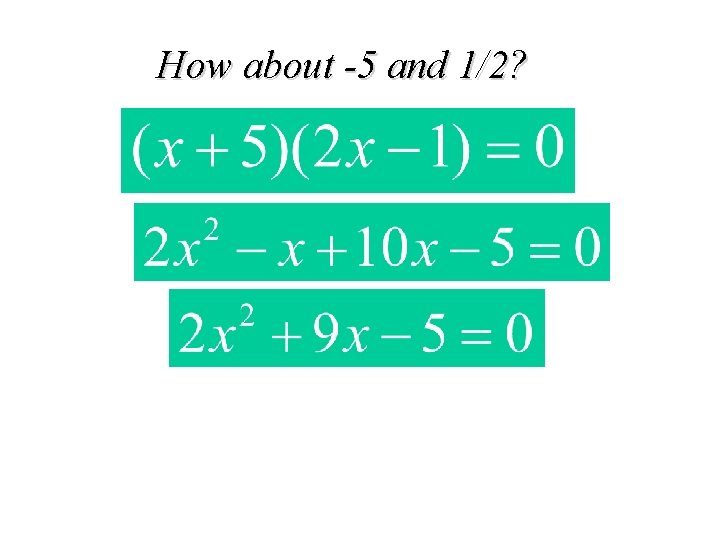
How about -5 and 1/2?
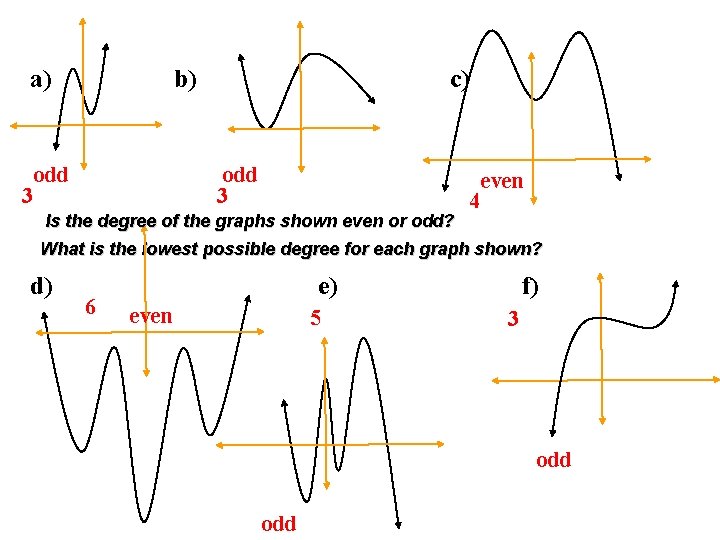
a) 3 b) odd c) odd 3 Is the degree of the graphs shown even or odd? 4 even What is the lowest possible degree for each graph shown? d) 6 e) even 5 f) 3 odd
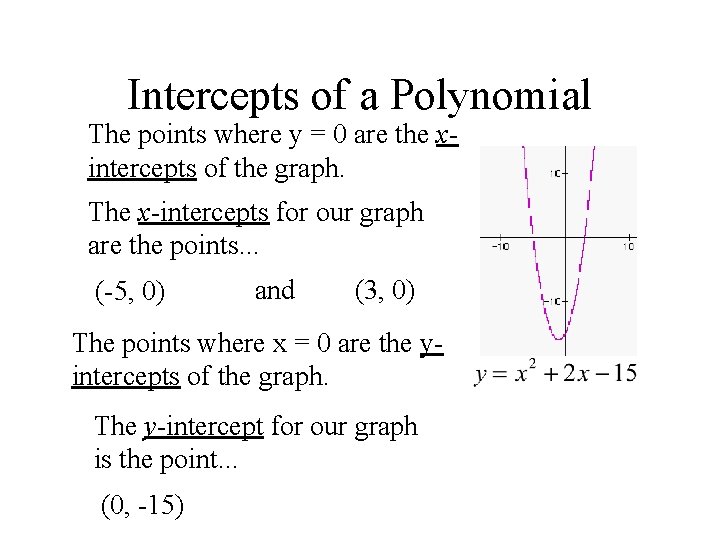
Intercepts of a Polynomial The points where y = 0 are the xintercepts of the graph. The x-intercepts for our graph are the points. . . (-5, 0) and (3, 0) The points where x = 0 are the yintercepts of the graph. The y-intercept for our graph is the point. . . (0, -15)

ØA graph with an odd degree will have ends in different directions. ØThink of any line (which has degree 1). ØA graph with an even degree will have ends in the same direction. ØThink of any parabola (which has degree 2). ØCount the “sections” to find the lowest possible degree of a polynomial graph.
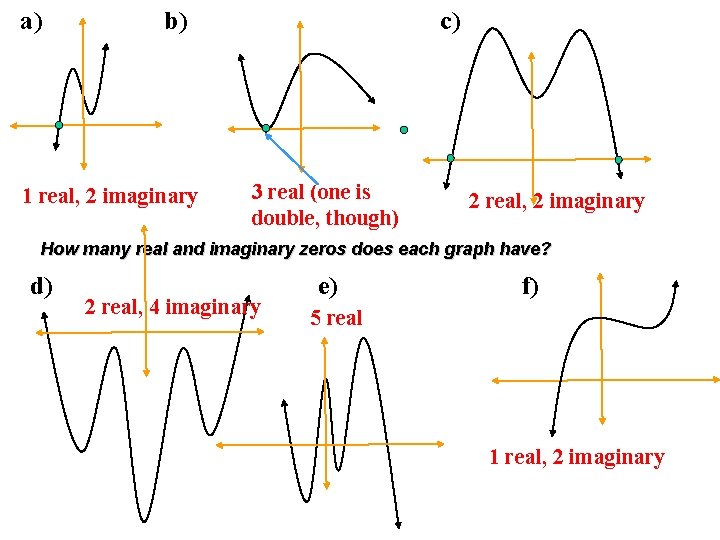
a) b) 1 real, 2 imaginary c) 3 real (one is double, though) 2 real, 2 imaginary How many real and imaginary zeros does each graph have? d) 2 real, 4 imaginary e) f) 5 real 1 real, 2 imaginary
- Slides: 13