Objectives The student will be able to describe

Objectives The student will be able to: • • describe the variation of the data. find the mean absolute deviation of a data set.

Measures of Variation Two formulas which find the dispersion of data about the mean: standard deviation – squares each difference from the mean to eliminate the negative differences. mean absolute deviation – uses absolute value of each difference from the mean to eliminate the negative differences.

Mean Absolute Deviation The average distance between each data value and the mean.

Mean Absolute Deviation MAD is a better measure of dispersion than the standard deviation when there are outliers in the data. An outlier is a data point which is far removed in value from the others in the data set.

Mean Absolute Deviation The bigger (>) the MAD the more variation. The smaller (<) the MAD the less variation.

Mean Absolute Deviation 1. Find the mean of the data. 2. Subtract the mean from each value – the result is called the deviation from the mean. 3. Take the absolute value of each deviation from the mean. 4. Find the sum of the absolute values. 5. Divide the total by the number of items.

Find the Mean Number of cell phone contacts stored in 8 friends phones : 52, 48, 60, 55, 59, 54, 58, 62 Find the mean: 52+48+60+55+59+54+58+62=56 8
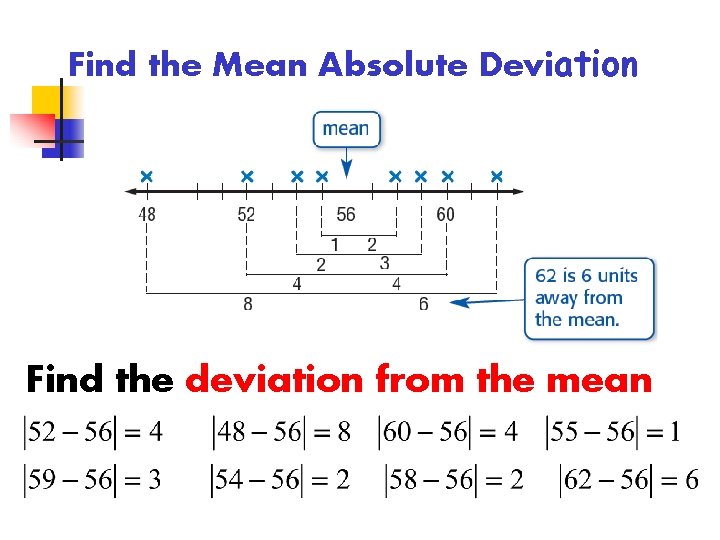
Find the Mean Absolute Deviation Find the deviation from the mean

Find the mean absolute deviation Find the sum of the absolute values: 8 + 4 + 2 + 1 + 2 + 3 + 4 + 6 = 30 Divide the sum by the number of data items: 30 = 3. 75 8 This means the average distance between each data value and the mean is 3. 75 contacts.

Standard Deviation shows the variation in data. If the data is close together, the standard deviation will be small. If the data is spread out, the standard deviation will be large. Standard Deviation is often denoted by the lowercase Greek letter sigma, .

The bell curve which represents a normal distribution of data shows what standard deviation represents. One standard deviation away from the mean ( ) in either direction on the horizontal axis accounts for around 68 percent of the data. Two standard deviations away from the mean accounts for roughly 95 percent of the data with three standard deviations representing about 99 percent of the data.
Analyzing the data: The standard deviation of quiz scores for Class A is about 1. 2. Describe the quiz scores that are within one standard deviation of the mean. Quiz Scores: 9, 8, 6, 7, 8, 9, 9, 10, 7, 10, 8, 8 Answer Now

Analyzing the data: Step 1: Find the mean Mean = 8. 25 Step 2: Find the range of values that are within one standard deviation of the mean. 8. 25 - 1. 2 = 7. 05 8. 25 + 1. 2 = 9. 45 Quiz scores that are between 7. 05 and 9. 45 are within one standard deviation of the mean.

Summary: As we have seen, standard deviation measures the dispersion of data. The greater the value of the standard deviation, the further the data tend to be dispersed from the mean.
- Slides: 14