Objectives Open GL drawing primitives and attributes Open

Objectives – Open. GL drawing primitives and attributes – Open. GL polygon face and culling – Open. GL hidden-surface removal – Constructing 3 D models in Open. GL – Collision detection @ 2017 by Jim X. Chen: jchen@cs. gmu. edu 1

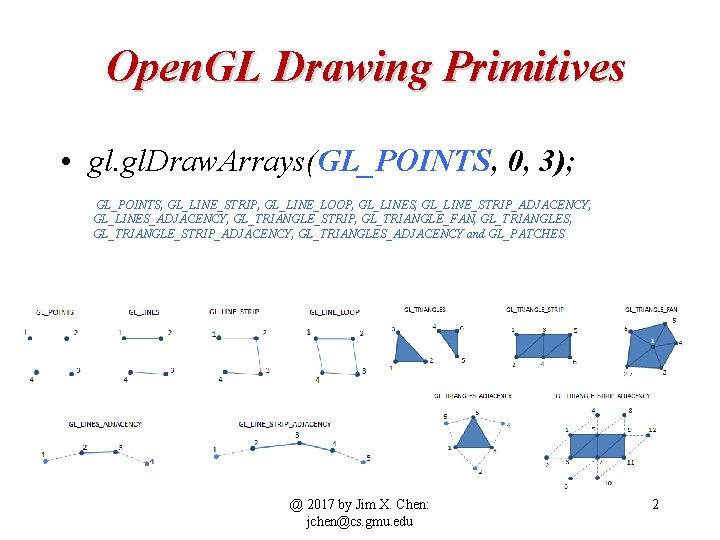
Open. GL Drawing Primitives • gl. Draw. Arrays(GL_POINTS, 0, 3); GL_POINTS, GL_LINE_STRIP, GL_LINE_LOOP, GL_LINES, GL_LINE_STRIP_ADJACENCY, GL_LINES_ADJACENCY, GL_TRIANGLE_STRIP, GL_TRIANGLE_FAN, GL_TRIANGLES, GL_TRIANGLE_STRIP_ADJACENCY, GL_TRIANGLES_ADJACENCY and GL_PATCHES @ 2017 by Jim X. Chen: jchen@cs. gmu. edu 2

The old way of doing it void gl. Begin(GLenum mode); mode: • GL_POINTS individual points • GL_LINES pairs of vertices interpreted as individual line segments • GL_POLYGON boundary of a simple, convex polygon • GL_TRIANGLES triples of vertices interpreted as triangles • GL_QUADS quadruples of vertices interpreted as four-sided polygons • GL_LINE_STRIP series of connected line segments • GL_LINE_LOOP same as above, with a segment added between last and first vertices • GL_TRIANGLE_STRIP linked strip of triangles • GL_TRIANGLE_FAN linked fan of triangles • GL_QUAD_STRIP linked strip of quadrilaterals @ 2017 by Jim X. Chen: jchen@cs. gmu. edu 3

Review: SPECIFYING A COLOR gl. Color 3 f(0. 0, 0. 0); draw_object(A); draw_object(B); gl. Color 3 f(1. 0, 0. 0); draw_object(C); gl. Color 3 f(0. 0, 0. 0); gl. Color 3 f(1. 0, 0. 0); gl. Color 3 f(0. 0, 1. 0); gl. Color 3 f(1. 0, 0. 0, 1. 0); gl. Color 3 f(0. 0, 1. 0); gl. Color 3 f(1. 0, 1. 0); A vertex color can be specified. A fragment color can be interpolated from primitive vertices. Colors are coupled with vertices in VAO/VBO. black red green yellow blue magenta cyan white @ 2017 by Jim X. Chen: jchen@cs. gmu. edu 4

DEPTH BUFFER (Z-BUFFER) gl. Clear. Color(0. 0, 0. 0); // RGBA, A=>alpha gl. Enable(GL_DEPTH_TEST); . . . while (1) { gl. Clear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT); draw_3 d_object_A(); draw_3 d_object_B(); } Color buffer Depth buffer @ 2017 by Jim X. Chen: jchen@cs. gmu. edu 5

Drawing Geometric Models DEPTH BUFFER (Z-BUFFER) void gl. Clear. Depth(GLdouble depth); If buffer is GL_DEPTH, drawbuffer must be zero, and value points to a single value to clear the depth buffer to. Color buffer Depth buffer @ 2017 by Jim X. Chen: : jchen@cs. gmu. edu 6. 6.

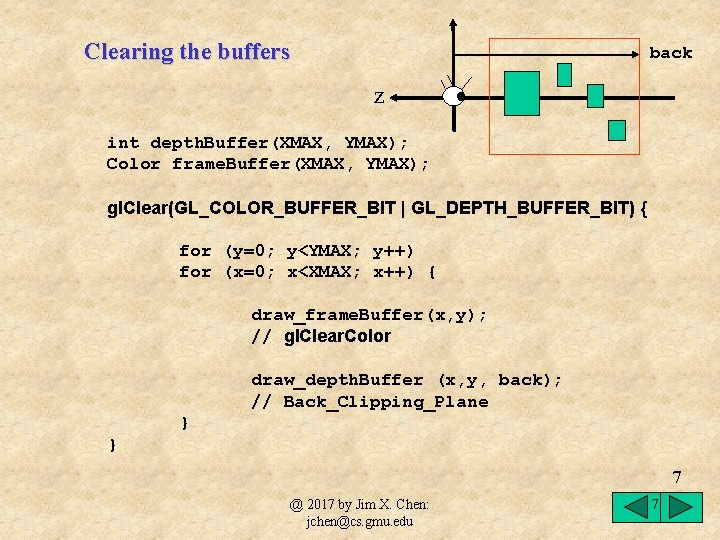
Clearing the buffers back z int depth. Buffer(XMAX, YMAX); Color frame. Buffer(XMAX, YMAX); gl. Clear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT) { for (y=0; y<YMAX; y++) for (x=0; x<XMAX; x++) { draw_frame. Buffer(x, y); // gl. Clear. Color draw_depth. Buffer (x, y, back); // Back_Clipping_Plane } } 7 @ 2017 by Jim X. Chen: jchen@cs. gmu. edu 7

THE Z-BUFFER ALGORITHM z float pixel. Depth; int depth. Buffer(XMAX, YMAX); Color frame. Buffer(XMAX, YMAX); for (each polygon) for (each pixel (x, y) in the polygon scan-conversion) { if (GL_DEPTH_TEST enabled) z. Buffer(x, y); // gl. Enable(GL_DEPTH_TEST); else draw_frame. Buffer(x, y); } z. Buffer(int x, int y) { pixel. Depth = polygon’s z-value at pixel (x, y); if (pixel. Depth < read_depth. Buffer(x, y)) { draw_depth. Buffer(x, y, pixel. Depth); draw_frame. Buffer(x, y); // gl. Color } } 8 @ 2017 by Jim X. Chen: jchen@cs. gmu. edu 8

Polygon’s z-value • Modify polygon-scan conversion algorithm: for each pixel (x, y) – Ax + By + Cz + D = 0 • z = f(x, y) = - (Ax + By +D)/C – zi+1 = zi + d //for a scan-line – d = -A/C @ 2017 by Jim X. Chen: jchen@cs. gmu. edu 9

Depth Test: J 2_5_Cone // clear both framebuffer and zbuffer gl. Clear(GL. GL_COLOR_BUFFER_BIT | GL. GL_DEPTH_BUFFER_BIT); // for testing hidden-surface removal if (cnt % 600 < 500) { gl. Enable(GL. GL_DEPTH_TEST); } else gl. Disable(GL. GL_DEPTH_TEST); @ 2017 by Jim X. Chen: jchen@cs. gmu. edu 10

Faces of a Polygon and Back-face Culling • Front face polygon has counterclockwise vertices, with normal facing viewer. In Open. GL, this can be defined. • void gl. Polygon. Mode(GLenum face, Glenum mode); face can be GL_FRONT_AND_BACK, GL_FRONT, or GL_BACK; mode can be GL_POINT, GL_LINE, or GL_FILL • void gl. Cull. Face(GLenum mode); Indicates which polygons should be discarded. The mode is either GL_FRONT, GL_BACK, or GL_FRONT_AND_BACK. To take effect, use gl. Enable(GL_CULL_FACE). @ 2017 by Jim X. Chen: jchen@cs. gmu. edu 11

J 2_5_Cone Polygon. Mode and Cull. Face // for testing polygon mode if (cnt % 100 > 50) gl. Polygon. Mode(GL. GL_FRONT_AND_BACK, GL. GL_LINE); else gl. Polygon. Mode(GL. GL_FRONT_AND_BACK, GL. GL_FILL); // for testing cull face if (cnt % 500 > 495) { gl. Enable(GL. GL_CULL_FACE); gl. Cull. Face(GL. GL_FRONT); } else if (cnt % 500 > 490) { gl. Enable(GL. GL_CULL_FACE); gl. Cull. Face(GL. GL_BACK); } else { gl. Disable(GL. GL_CULL_FACE); } @ 2017 by Jim X. Chen: jchen@cs. gmu. edu 12

Drawing Geometric Models CIRCLE, CONE, CYLINDER, SPHERE, AND ANIMATION Circle Cone Cylinder Sphere @ 2017 by Jim X. Chen: : jchen@cs. gmu. edu 13.

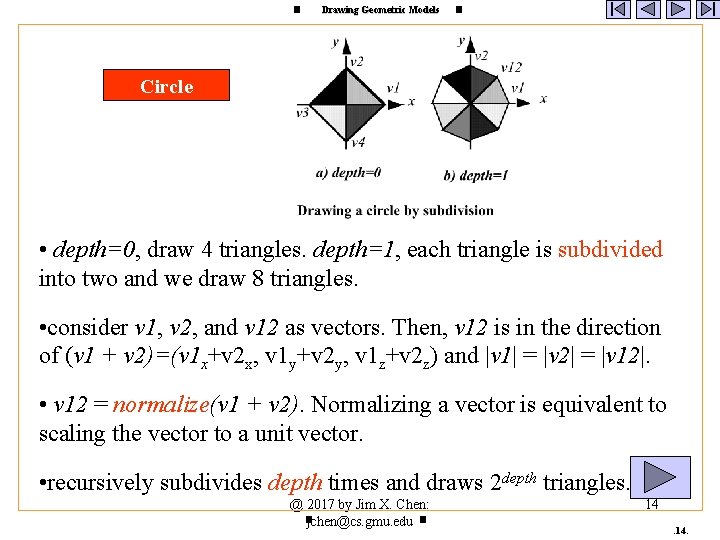
Drawing Geometric Models Circle • depth=0, draw 4 triangles. depth=1, each triangle is subdivided into two and we draw 8 triangles. • consider v 1, v 2, and v 12 as vectors. Then, v 12 is in the direction of (v 1 + v 2)=(v 1 x+v 2 x, v 1 y+v 2 y, v 1 z+v 2 z) and |v 1| = |v 2| = |v 12|. • v 12 = normalize(v 1 + v 2). Normalizing a vector is equivalent to scaling the vector to a unit vector. • recursively subdivides depth times and draws 2 depth triangles. @ 2017 by Jim X. Chen: : jchen@cs. gmu. edu 14.

Drawing Geometric Models Cone raise the center of the circle along the z axis Example: J 2_5_Cone // make sure the cone is within the viewing volume gl. Ortho(-Width/2, -Height/2, -Width/2, Width/2); @ 2017 by Jim X. Chen: : jchen@cs. gmu. edu 15.

J 2_5_Cone private void subdivide. Cone(float v 1[], float v 2[], int depth) { float v 0[] = {0, 0, 0}; float v 12[] = new float[3]; if (depth==0) { gl. Color 3 d(v 1[0]*v 1[0], v 1[1]*v 1[1], v 1[2]*v 1[2]); drawtriangle(v 2, v 1, v 0); // bottom cover of the cone v 0[2] = 1; // height of the cone, the tip on z axis drawtriangle(v 1, v 2, v 0); // side cover of the cone return; } for (int i = 0; i<3; i++) v 12[i] = v 1[i]+v 2[i]; normalize(v 12); subdivide. Cone(v 1, v 12, depth-1); subdivide. Cone(v 12, v 2, depth-1); } @ 2017 by Jim X. Chen: jchen@cs. gmu. edu 16

Drawing Geometric Models Cylinder draw a circle at z=0, draw another circle at z=1. If we connect the rectangles of the same vertices on the edges of the two circles, we have a cylinder Example: J 2_6_Cylinder // make sure the cone is within the viewing volume gl. Ortho(-Width/2, -Height/2, -Width/2, Width/2); @ 2017 by Jim X. Chen: : jchen@cs. gmu. edu 17.

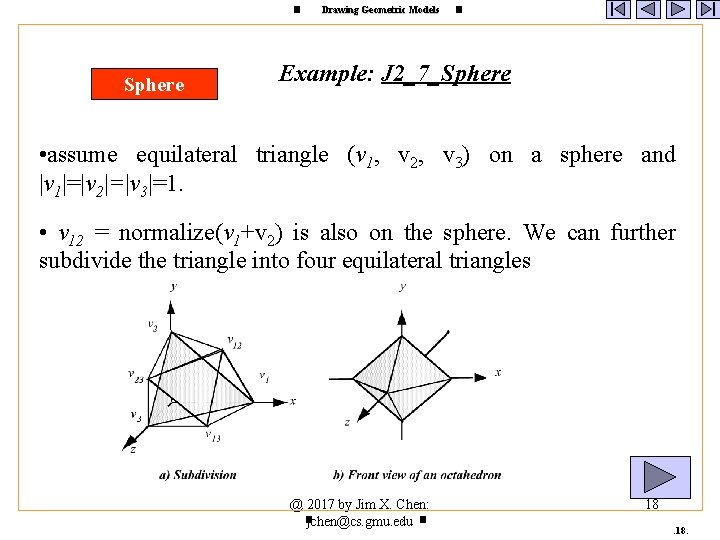
Drawing Geometric Models Sphere Example: J 2_7_Sphere • assume equilateral triangle (v 1, v 2, v 3) on a sphere and |v 1|=|v 2|=|v 3|=1. • v 12 = normalize(v 1+v 2) is also on the sphere. We can further subdivide the triangle into four equilateral triangles @ 2017 by Jim X. Chen: : jchen@cs. gmu. edu 18.

J 2_7_Sphere private void subdivide. Sphere( float v 1[], float v 2[], float v 3[], long depth) { float v 12[] = new float[3], v 23[] = new float[3], v 31[] = new float[3]; int i; if (depth==0) { gl. Color 3 f(v 1[0]*v 1[0], v 2[1]*v 2[1], v 3[2]*v 3[2]); drawtriangle(v 1, v 2, v 3); return; } for (i = 0; i<3; i++) { v 12[i] = v 1[i]+v 2[i]; v 23[i] = v 2[i]+v 3[i]; v 31[i] = v 3[i]+v 1[i]; } normalize(v 12); normalize(v 23); normalize(v 31); subdivide. Sphere(v 1, v 12, v 31, depth-1); subdivide. Sphere(v 2, v 23, v 12, depth-1); subdivide. Sphere(v 3, v 31, v 23, depth-1); subdivide. Sphere(v 12, v 23, v 31, depth-1); } @ 2017 by Jim X. Chen: jchen@cs. gmu. edu 19

Drawing Geometric Models More Hidden-surface Removal Ø view point at the origin and the models are in the negative z axis Ø render the models in the order of their distances to the view point along z axis from the farthest to the closest Ø build up a box (bounding volume) with the faces perpendicular to the x, y, or z axis to bound a 3 D model Ø compare the minimum and maximum bounds in the z direction between boxes to decide which model should be rendered first Ø Using bounding volumes to decide priority of rendering is also known as minmax testing. z @ 2017 by Jim X. Chen: : jchen@cs. gmu. edu 20.

Collision Detection z v collision detection avoid two models in an animation penetrating each other v we can use their bounding volumes to decide their physical distances and collision v bounding volume can be in a different shape other than a box, such as a sphere. v We may use multiple spheres with different radii to more accurately bound a model, but the collision detection would be more complex. J 2_11_Cone. Solar. Collision @ 2017 by Jim X. Chen: jchen@cs. gmu. edu 21