Objectives Determine realistic domain restrictions of a volume

Objectives: • Determine realistic domain restrictions of a volume function. • Define and examine the two forms of a polynomial function.

POLYNOMIAL FUNCTIONS A POLYNOMIAL FUNCTION is a function that can be expressed by a product of linear factors multiplied by a constant. A linear factor of a function is any factor of the form (x – r). r can be a real or complex number.

Classwork: Section 6. 1 Exploration

Factored Form of a Polynomial Function:

Expanded Form of a Polynomial Function: If f is a polynomial function, then it can be written in the expanded form: n must be a positive integer All of these coefficients are real numbers

POLYNOMIAL FUNCTIONS What is the degree, leading coefficient, and constant term of 3 x 5 – 3 x + 2 ? Degree is 5 Leading coefficient is 3 Constant term is 2

Polynomial Functions • Exponents must be non-negative integer exponents • Can not have variables in the denominator • Can not have radicals

Determine which of the following are polynomial functions. If it is a polynomial, state its degree. A polynomial of degree 4. We can write in an x 0 since this = 1. x 0 A polynomial of degree 0. Not a polynomial because of the square root. The power is NOT an integer Not a polynomial because of the x in the denominator. The power is negative

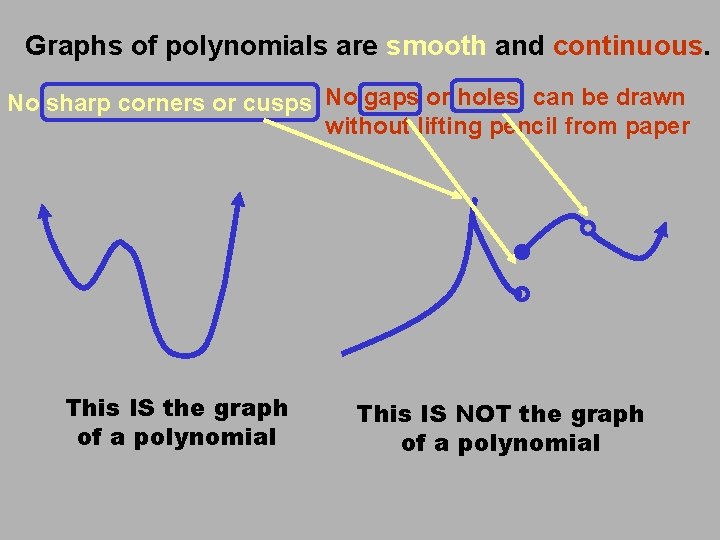
Graphs of polynomials are smooth and continuous. No sharp corners or cusps No gaps or holes, can be drawn without lifting pencil from paper This IS the graph of a polynomial This IS NOT the graph of a polynomial

SPECIAL POLYNOMIAL FUNCTIONS Polynomial functions with a degree of 1 are called LINEAR POLYNOMIAL FUNCTIONS Polynomial functions with a degree of 2 are called QUADRATIC POLYNOMIAL FUNCTIONS Polynomial functions with a degree of 3 are called CUBIC POLYNOMIAL FUNCTIONS Polynomial functions with a degree of 4 are called QUARTIC POLYNOMIAL FUNCTIONS

POLYNOMIAL FUNCTIONS GENERAL SHAPES OF POLYNOMIAL FUNCTIONS f(x) = 3 Constant Function Degree = 0 Max. Zeros: 0

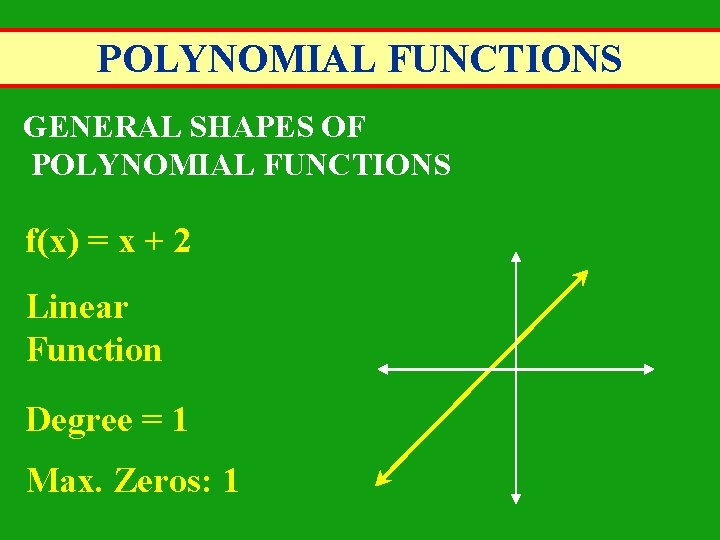
POLYNOMIAL FUNCTIONS GENERAL SHAPES OF POLYNOMIAL FUNCTIONS f(x) = x + 2 Linear Function Degree = 1 Max. Zeros: 1

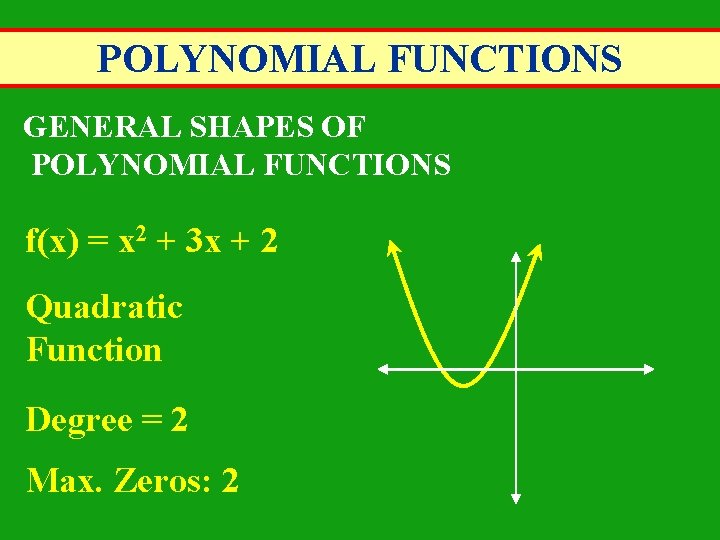
POLYNOMIAL FUNCTIONS GENERAL SHAPES OF POLYNOMIAL FUNCTIONS f(x) = x 2 + 3 x + 2 Quadratic Function Degree = 2 Max. Zeros: 2

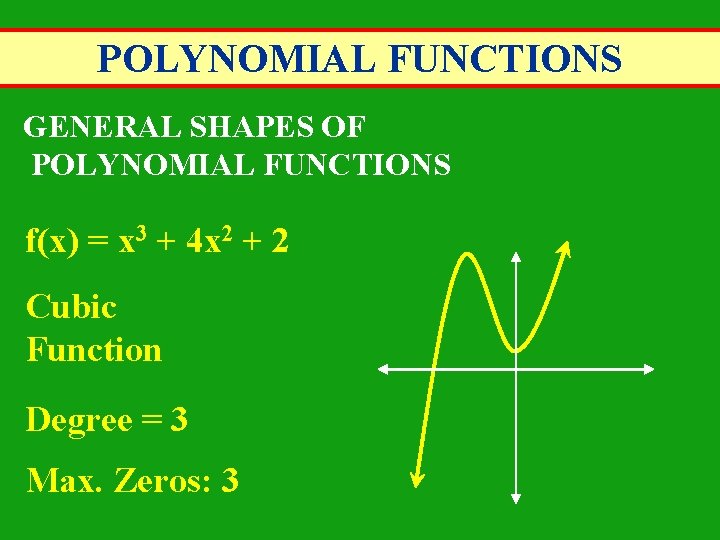
POLYNOMIAL FUNCTIONS GENERAL SHAPES OF POLYNOMIAL FUNCTIONS f(x) = x 3 + 4 x 2 + 2 Cubic Function Degree = 3 Max. Zeros: 3

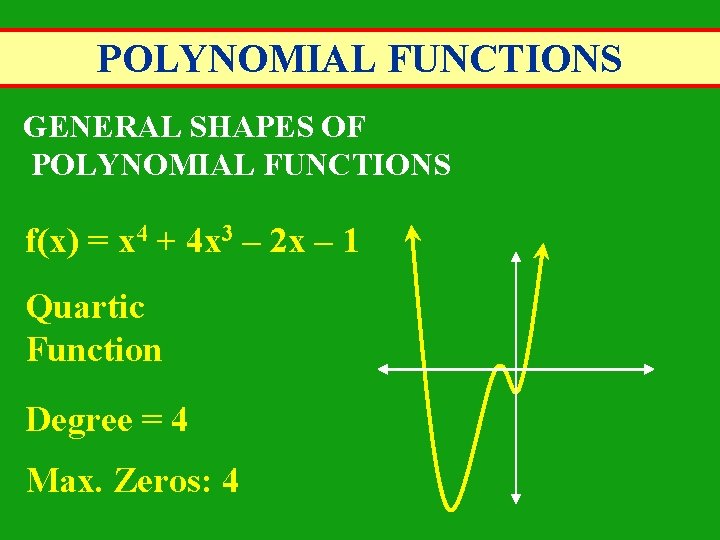
POLYNOMIAL FUNCTIONS GENERAL SHAPES OF POLYNOMIAL FUNCTIONS f(x) = x 4 + 4 x 3 – 2 x – 1 Quartic Function Degree = 4 Max. Zeros: 4

Homework: Section 6. 1 Practice and Apply