Objectives Decide whether a relation between two variables

Objectives • Decide whether a relation between two variables represents a function • Use function notation and evaluate functions • Find the domain & range of functions • Function operations: Sum, Difference, Product, Quotient 1

PART 1: FUNCTIONS 2

Introduction to Functions Relation: Ordered pairs of (INPUT, OUTPUT) Function: Relation in which the inputs are restricted so that there are no repeats in the input. Also…there is some relation that matches each item from one set with exactly one item from a different set. 3

Introduction to Functions To determine whether or not a relation is a function, you must decide whether each input value is matched with exactly one output value. When any input value is matched with two or more output values, the relation is not a function; i. e. , the same input value has two or more different kinds of output values. Example: {(1, 1), (2, 4), (3, 7)} {(1, 1), (1, 2), (1, 3)} 4

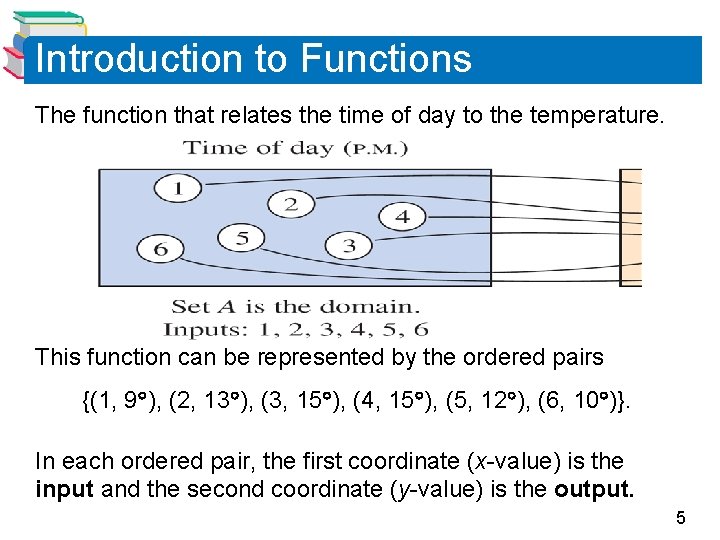
Introduction to Functions The function that relates the time of day to the temperature. This function can be represented by the ordered pairs {(1, 9 ), (2, 13 ), (3, 15 ), (4, 15 ), (5, 12 ), (6, 10 )}. In each ordered pair, the first coordinate (x-value) is the input and the second coordinate (y-value) is the output. 5

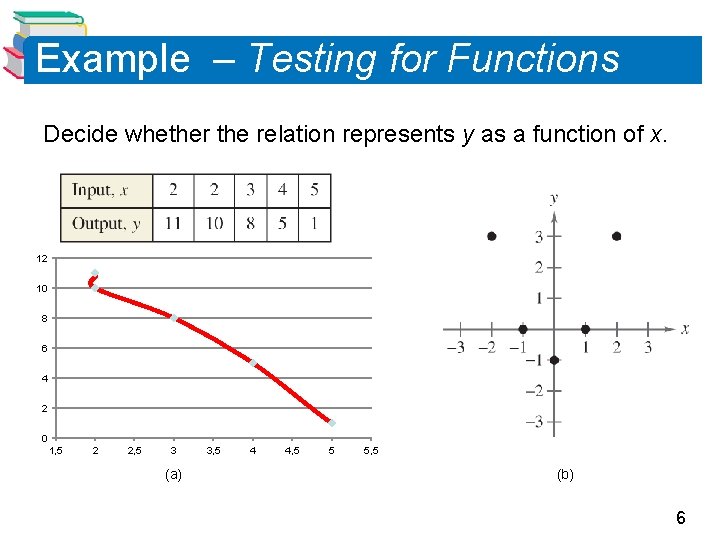
Example – Testing for Functions Decide whether the relation represents y as a function of x. 12 10 8 6 4 2 0 1, 5 2 2, 5 3 (a) 3, 5 4 4, 5 5 5, 5 (b) 6

Introduction to Functions In algebra, we typically represent functions using two variables: independent variable (input) dependent variable (output) Given: Domain is the set of all values of the independent variable (x) Range is the set of all values of the dependent variable (y). y = x 2 y is a function of x. x = independent y = dependent Domain = Range = 7

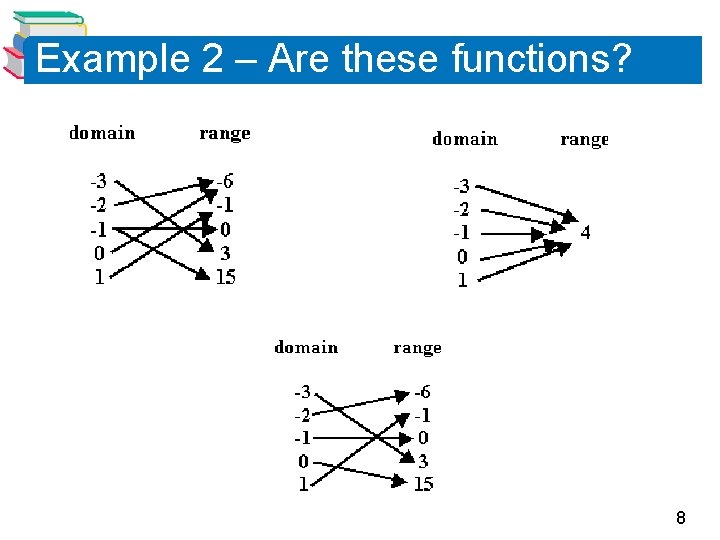
Example 2 – Are these functions? 8

Now you try… 9

The Graph of a Function • By the definition of a function, at most one y-value corresponds to a given x-value. It follows, then, that a vertical line can intersect the graph of a function at most once. This leads to the Vertical Line Test for functions. • 10

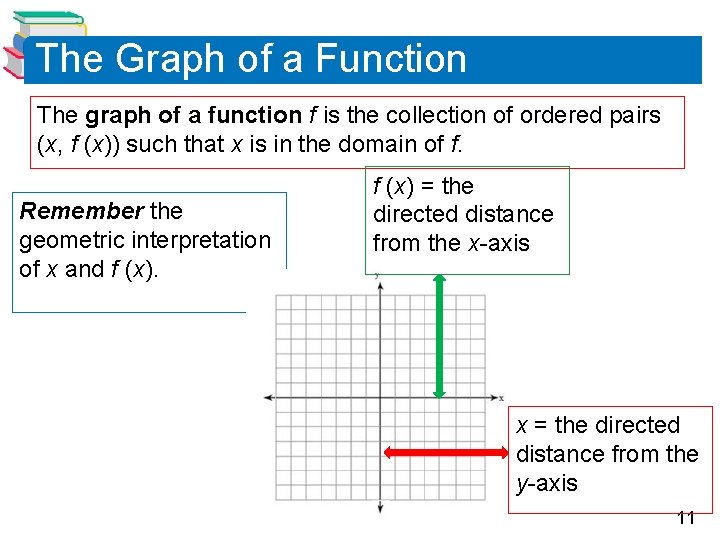
The Graph of a Function The graph of a function f is the collection of ordered pairs (x, f (x)) such that x is in the domain of f. Remember the geometric interpretation of x and f (x) = the directed distance from the x-axis x = the directed distance from the y-axis 11

Example 3 – Vertical Line Test for Functions • Use the Vertical Line Test to decide whether the graphs represent y as a function of x. 12

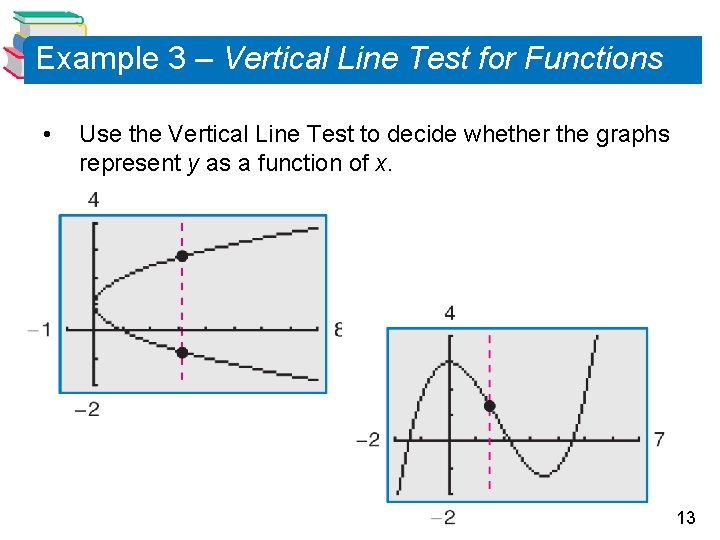
Example 3 – Vertical Line Test for Functions • Use the Vertical Line Test to decide whether the graphs represent y as a function of x. 13

The Domain of a Function DOMAIN: The set of all possible input values for the given function. (Restrictions may apply) Restriction #1: Divide by zero Example: Implied Domain excludes x-values that All real numbers except x = 2 result in division by zero. x = 2 14

The Domain of a Function Restriction #2: Square root of negative numbers. Example: Domain excludes x-values that results in even roots of negative numbers: x 0 In general, the domain of a function excludes values that would cause division by zero or result in the even root of a negative number. 15

The Range of a Function The range of a function is the set of all possible outputs given the input (the domain). (Restrictions may result from domain) Domain: All real numbers except x = 2 Range: All real numbers except y = 0 16

The Range of a Function Example: . Domain excludes x-values that results in even roots of negative numbers: x 0 What is the range of this function? 17

Example 5 –Domain & Range of a Function Find the Domain & Range of each function. a. f : {(– 3, 0), (– 1, 4), (0, 2), (2, 2), (4, – 1)} b. g (x) = – 3 x 2 + 4 x + 5 c. 18

Function Notation When an equation is used to represent a function, it is convenient to name the function so that it can be referenced easily. For example, you know that the equation y = 1 – x 2 describes y as a function of x. Suppose you give this function the name “f ”. Then you can use the following function notation. Input x Output f (x) Equation f (x) = 1 – x 2 19

Function Notation The symbol f (x) is read as the value of f at x or simply f of x. The symbol f (x) corresponds to the y-value for a given x. So, you can write y = f (x). NOTE: f is the name of the function, but f (x) is the output value of the function given the input value x. Given: f (x) = 3 – 2 x f (– 1) = f (0) = 20

Function Notation Although f is often used as a function name and x is often used as the independent variable, any set of letters can be used. For example: f (x) = x 2 – 4 x + 7 f (t) = t 2 – 4 t + 7 g(s) = s 2 – 4 s + 7 all define the same function. 21

Function Notation In fact, the role of the independent variable is that of a “placeholder. ” Consequently, the function could be written as f ( ) = ( )2 – 4 ( ) + 7. 22

Example – Evaluating a Function Let g (x) = –x 2 + 4 x + 1. Find each value of the function. a. g (2) b. g (t) c. g (x + 2) 23

Now you try… 24