Objectives 1 Use interval notation 2 Solve linear

Objectives: 1. Use interval notation. 2. Solve linear inequalities and compound linear inequalities. 3. Find exact solutions of quadratic and factorable inequalities. 2. 5 INEQUALITIES

Interval Notation [ c , d ] indicates ( c , d ) indicates [ c , d ) indicates ( c , d ] indicates c≤x≤d c<x<d c≤x<d c<x≤d [ c , d ] is called a closed interval, ( c , d ) is called an open interval, and the remaining two are called half open.

Interval Notation ( −∞ , 2 ] x≤ 2 ( − 3 , ∞ ) x >− 3 (−∞ , ∞ ) All Reals

Compound Inequality The statement b < c < d is called a compound inequality because b < c and c < d simultaneously. When solving an inequality, remember to reverse the inequality symbol when multiplying or dividing by a negative.

Example #1 Solving a Compound Linear Inequality Solve.

Example #2 Solving a Compound Linear Inequality Solve. If the variable only occurs in the middle, the inequality doesn’t need to be split up to be solved. The compound inequality can be solved by subtracting 4 from all three parts and dividing by a -3.

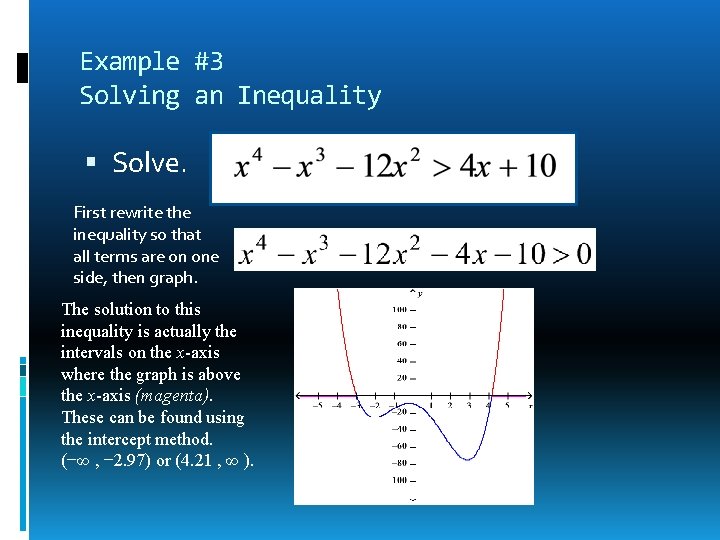
Example #3 Solving an Inequality Solve. First rewrite the inequality so that all terms are on one side, then graph. The solution to this inequality is actually the intervals on the x-axis where the graph is above the x-axis (magenta). These can be found using the intercept method. (−∞ , − 2. 97) or (4. 21 , ∞ ).

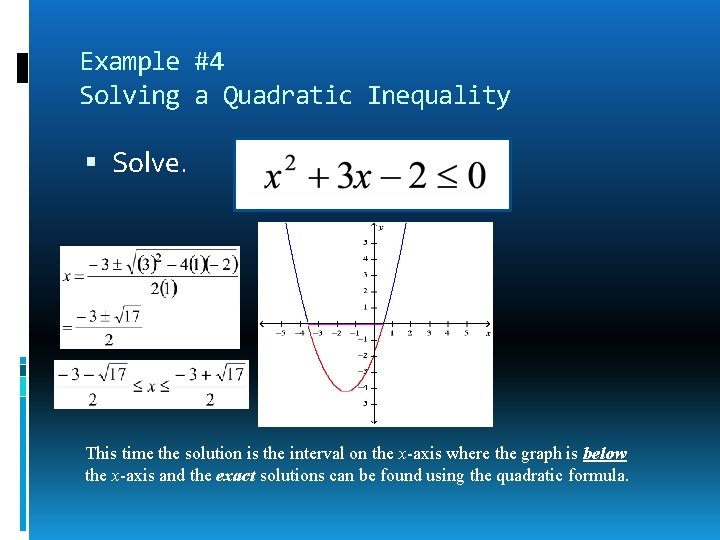
Example #4 Solving a Quadratic Inequality Solve. This time the solution is the interval on the x-axis where the graph is below the x-axis and the exact solutions can be found using the quadratic formula.

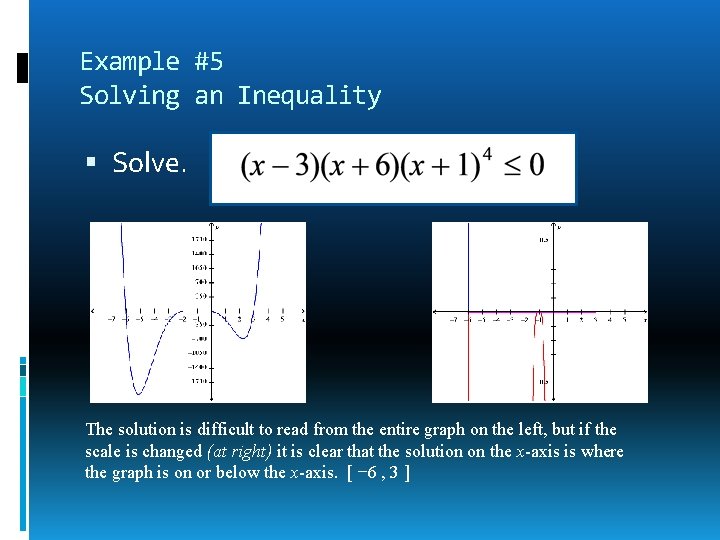
Example #5 Solving an Inequality Solve. The solution is difficult to read from the entire graph on the left, but if the scale is changed (at right) it is clear that the solution on the x-axis is where the graph is on or below the x-axis. [ − 6 , 3 ]

Example #6 Application A projectile is fired straight upward from ground level with initial velocity 160 feet per second. Its height in feet after x seconds is modeled by: During what time interval will the height of the projectile be greater than 336 feet?

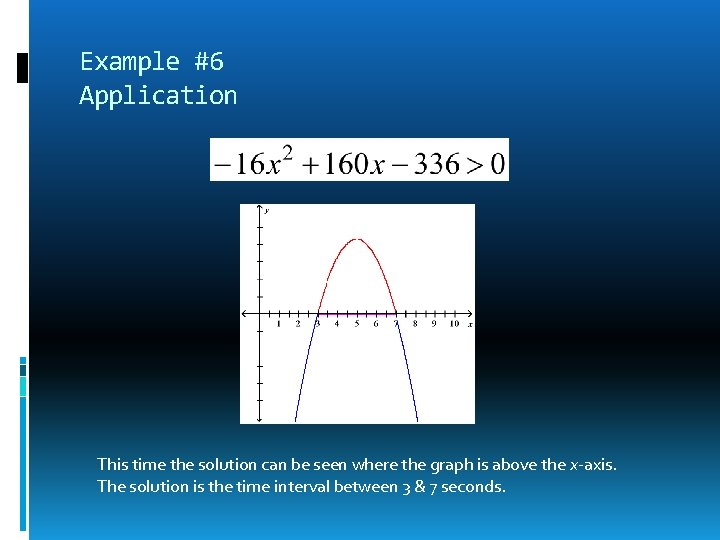
Example #6 Application This time the solution can be seen where the graph is above the x-axis. The solution is the time interval between 3 & 7 seconds.