Objectives 1 Recognize and extend an arithmetic sequence

Objectives: 1. Recognize and extend an arithmetic sequence 2. Find a given term of an arithmetic sequence.

A sequence is a list of numbers that often forms a pattern. Ø Example: 2, 4, 6, 8, … Each number in a sequence is a term. Ø Example: Ø 2 (1 st term), Ø 4 (2 nd term), Ø 6 (3 rd term), Ø 8 (4 th term)…

Arithmetic Sequence= A pattern that is formed by adding or subtracting by the same number over and over again. Common Difference (d)=the number you are continuously adding or subtracting

1. Determine whether the sequence appears to be an arithmetic sequence. 2. If so, find the common difference 3. Then find the next THREE TERMS. 1) 9, 13, 17, 21, 25, 29, 33, … +4 +4 +4 2) +4 +4 +4 10, 8, 5, 1, … – 2 – 3 – 4 Non-Arithmetic!

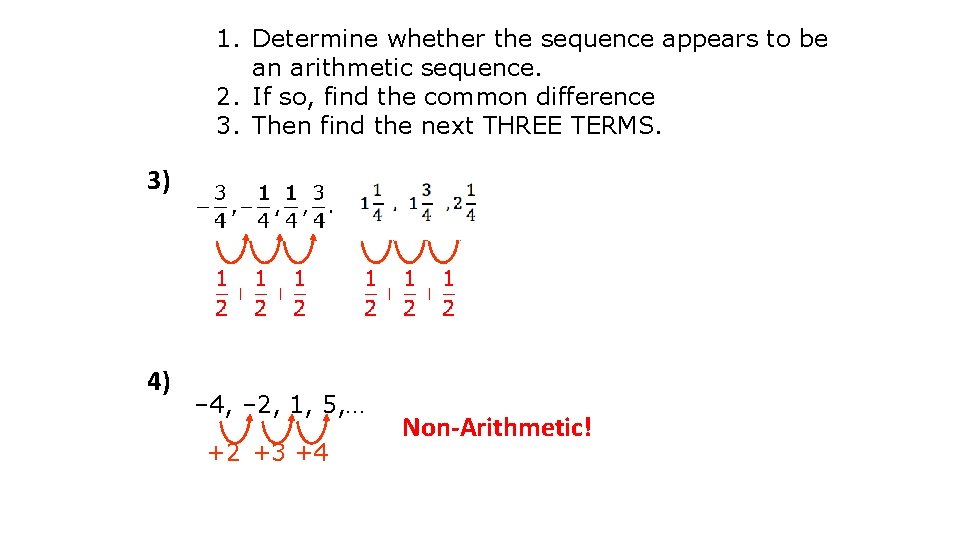
1. Determine whether the sequence appears to be an arithmetic sequence. 2. If so, find the common difference 3. Then find the next THREE TERMS. 3) 4) – 4, – 2, 1, 5, … +2 +3 +4 Non-Arithmetic!

The variable a is often used to represent terms in a sequence. a 1 = 1 st term a 2 = 2 nd term a 3 = 3 rd term, etc. To find a term we don’t know we often say we want to find the nth term, where “n” is the number term we are looking for.

The following formula can be used to find any term in an arithmetic sequence: Term you want = 1 st term + (term you want– 1)(pattern) *You do not need to memorize this! It is on your formula sheet!

Examples: 5) 6) Find the 16 th term: 4, 8, 12, 16, … Find the 20 th term: 4, 8, 12, 16, …

Examples: 7) Find the 18 th term: 11, 5, – 1, – 7, … 8) Find the 60 th term: 11, 5, – 1, – 7, …

Examples: 9) Find the 25 th term: a 1 = – 5; d = – 2 10) Find the 35 th term: a 1 = – 5; d = – 2