Objective To use intersection and union to simplify

Objective- To use intersection and union to simplify problems involving sets. Operations with Sets A = { 1, 2, 3 , 4, 5} B = { 2, 4, 6, 8, 10} C = { 5, 6, 7, 8} Intersection ( ) ( and ) - the elements which are common to both sets. 1) A B = { 2, 4} 2) B C = { 6, 8} 3) A C ={ 5 } 4) (A B) C { 2, 4} { 5, 6, 7, 8} { } or “empty set” or O or “null set”

Operations with Sets A = { 1, 2, 3 , 4, 5} B = { 2, 4, 6, 8, 10} C = { 5, 6, 7, 8} Union ( ) ( or ) - the combined set of elements from two sets with no duplication of elements. 1) A B = { 1, 2, 3, 4, 5, 6, 8, 10} 2) B C = { 2, 4, 5, 6, 7, 8, 10} 3) A C = { 1, 2, 3, 4, 5, 6, 7, 8}

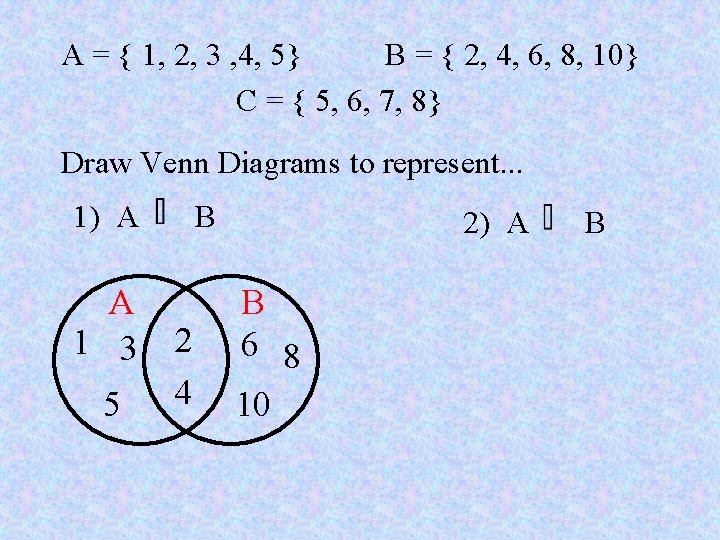
A = { 1, 2, 3 , 4, 5} B = { 2, 4, 6, 8, 10} C = { 5, 6, 7, 8} Draw Venn Diagrams to represent. . . 1) A A 1 3 5 B 2 4 2) A B 6 8 10 B

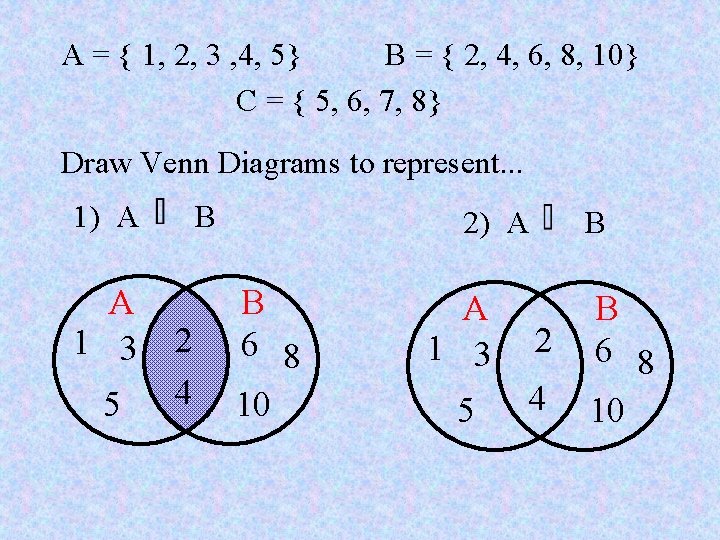
A = { 1, 2, 3 , 4, 5} B = { 2, 4, 6, 8, 10} C = { 5, 6, 7, 8} Draw Venn Diagrams to represent. . . 1) A A 1 3 5 B 2 4 2) A B 6 8 10 B A 1 3 2 5 4 B 6 8 10

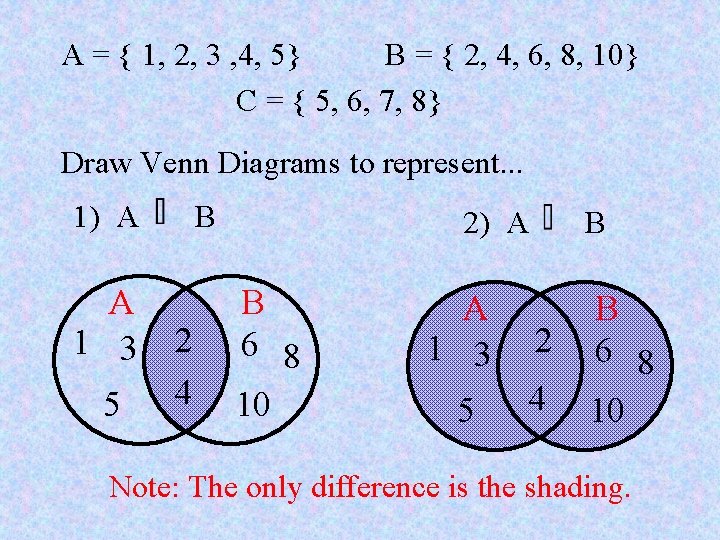
A = { 1, 2, 3 , 4, 5} B = { 2, 4, 6, 8, 10} C = { 5, 6, 7, 8} Draw Venn Diagrams to represent. . . 1) A A 1 3 5 B 2 4 2) A B 6 8 10 B A 1 3 2 5 4 B 6 8 10 Note: The only difference is the shading.

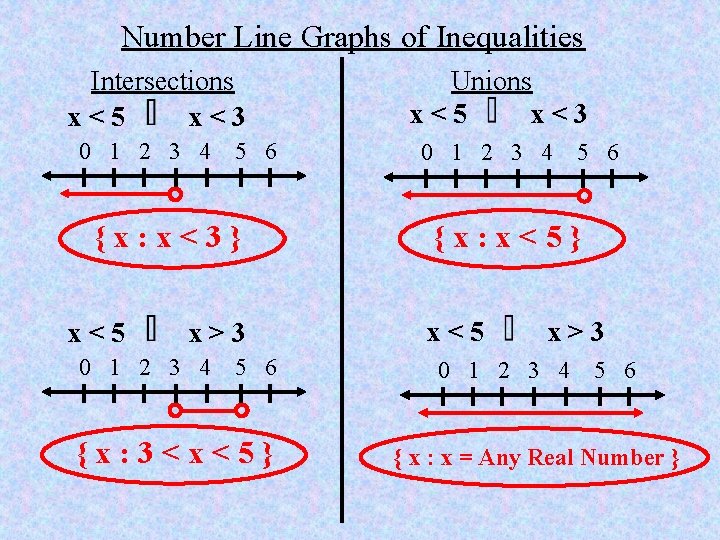
Number Line Graphs of Inequalities Intersections x<5 x<3 0 1 2 3 4 5 6 {x: x<3} x<5 x>3 0 1 2 3 4 5 6 {x: 3<x<5} Unions x<5 x<3 0 1 2 3 4 5 6 {x: x<5} x<5 x>3 0 1 2 3 4 5 6 { x : x = Any Real Number }

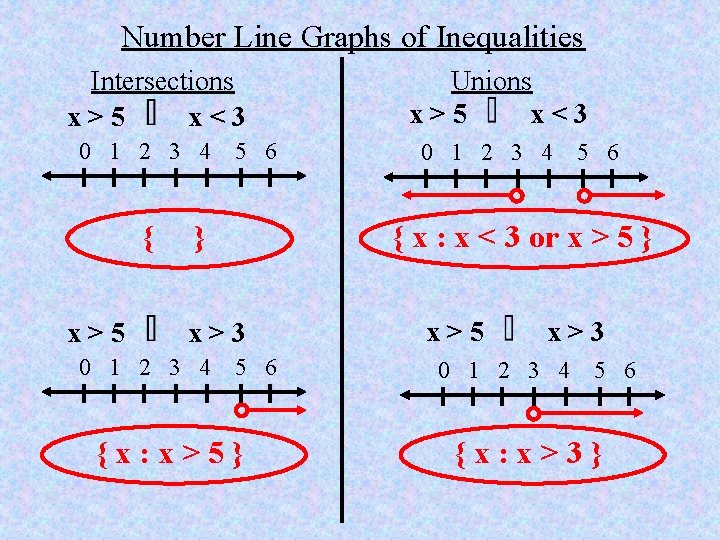
Number Line Graphs of Inequalities Intersections x>5 x<3 0 1 2 3 4 { x>5 5 6 } x>3 0 1 2 3 4 5 6 {x: x>5} Unions x>5 x<3 0 1 2 3 4 5 6 { x : x < 3 or x > 5 } x>5 x>3 0 1 2 3 4 5 6 {x: x>3}