Objective of Computer Vision The field of computer

Objective of Computer Vision • The field of computer vision can be divided into two areas – Image enhancement – Image analysis Here we concentrate on fast methods typical for robot soccer and robot theatre applications

Binary image processing Image with two gray levels 0 and 1 n It contains the basic terms and concepts used in machine vision. n Its techniques are used in all aspects of a vision system. n Small memory requirements n Fast execution time n
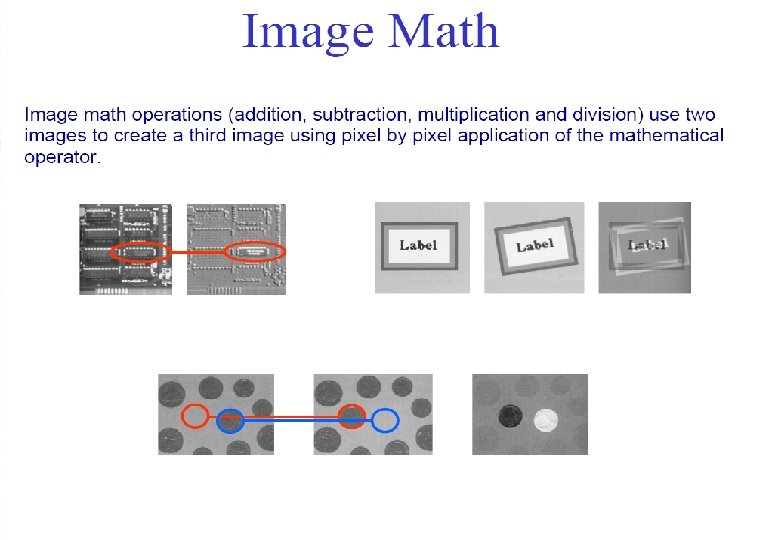


n Gray level image vs. binary image

Image Enhancement
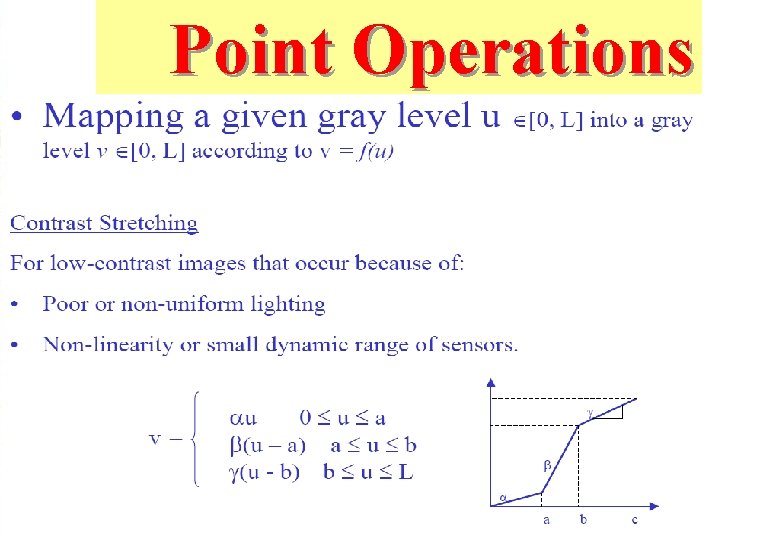
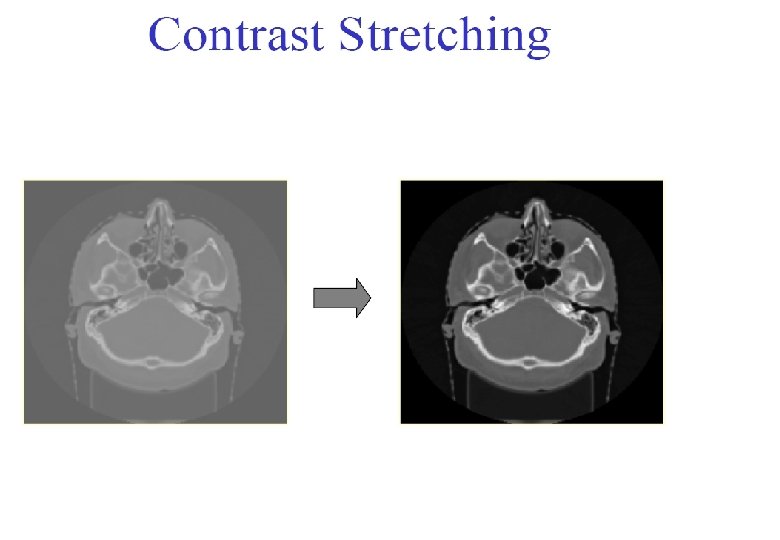
Point Operations

Region and segmentation n n Region ( ) l A subset of an image Segmentation l Grouping of pixels into regions such that
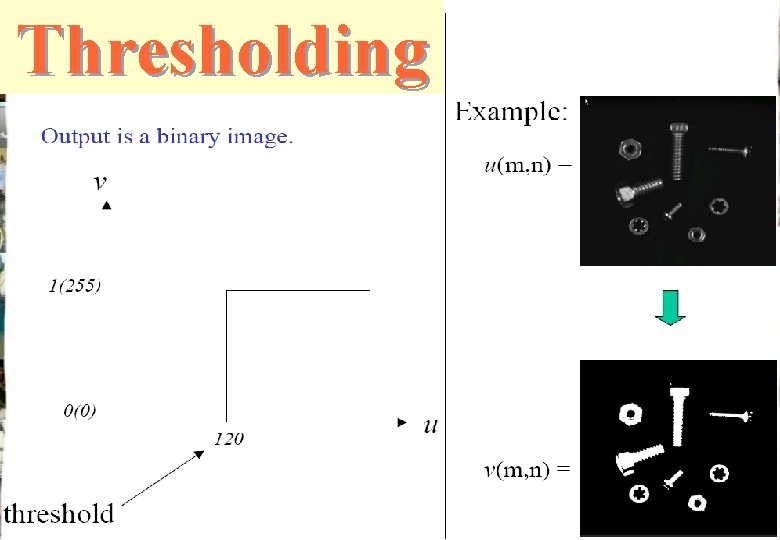
Thresholding

Thresholding n n Thresholding : l A method to convert a gray scale image into a binary image for object-background separation : Thresholded gray image l Obtained using a threshold T for the original gray image. n l : Binary image Equivalent to .

n Three types of thresholding where Z is a set of which elements are integer-valued intervals.
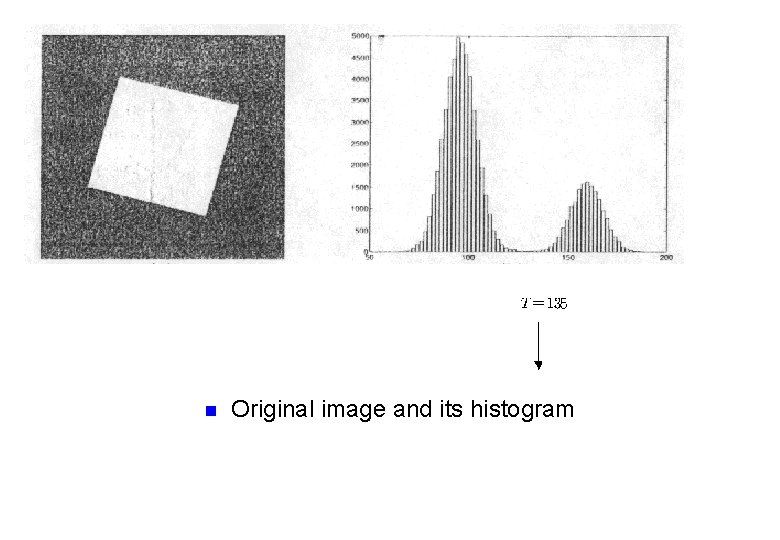
n Original image and its histogram
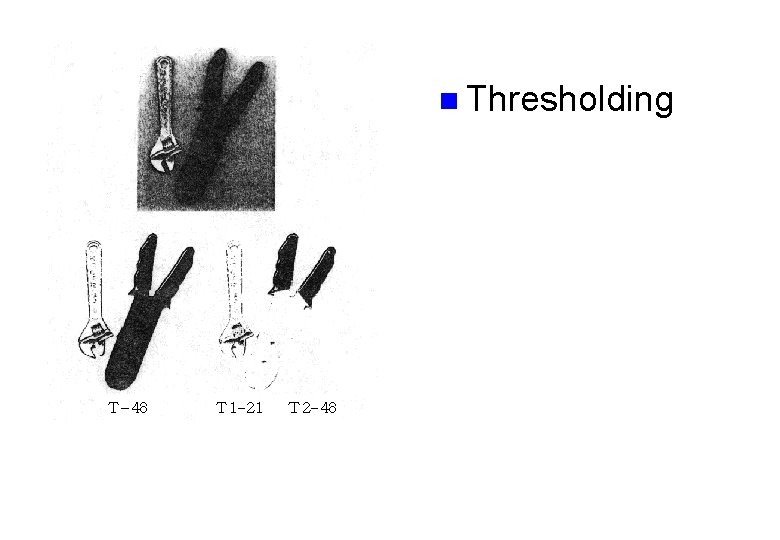
n Thresholding
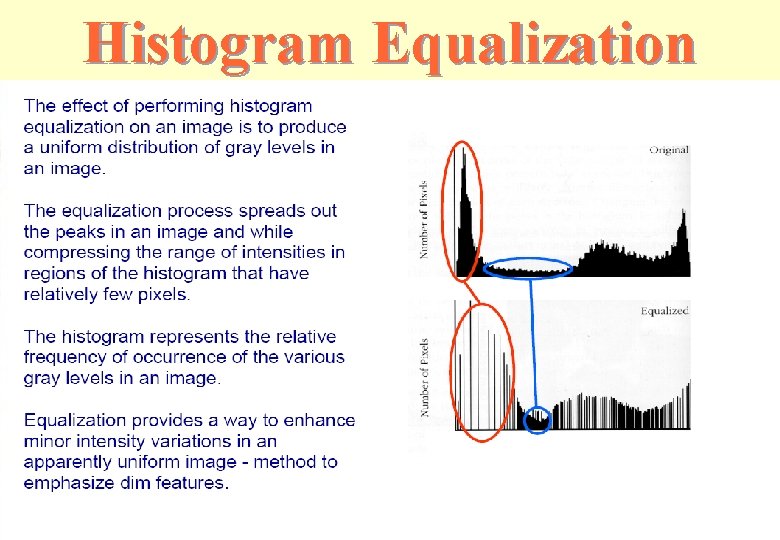
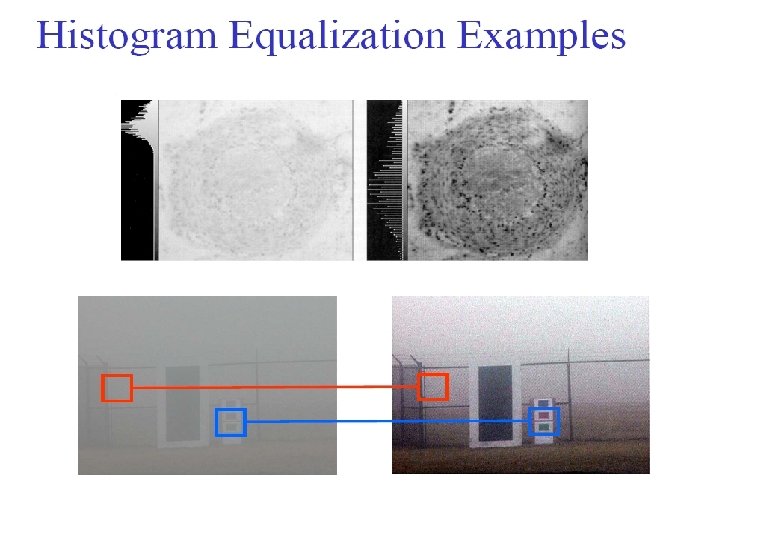
Histogram Equalization H

Vision System of Soccer Robot
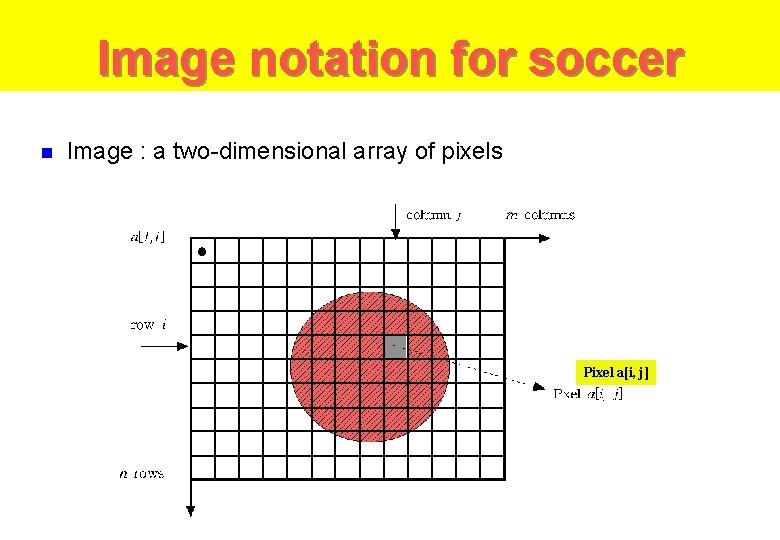
Image notation for soccer n Image : a two-dimensional array of pixels Pixel a[i, j]

Geometric properties n In many cases, some simple features of regions are useful to: determine the locations of objects, l and to recognize objects. l n Geometric properties: l Size l Position l Orientation

Size and position n Given an m x n binary image, l Size (area) A : zero-order moment Total size is number of black dots l Position : the center of area Average in x Average in y

Example

How to calculate line orientation? Step 1: calculate a, b, c coefficients l The center of object : Let l By the least-squares fit of the line, l Step 2: calculate angle, line orientation

Size filter for Noise removal n n It can effectively remove noise after component algorithm labeling. If objects of interest have sizes greater than T, all components below T are removed by changing the corresponding pixels’ values to 0. A noisy binary image and the resulting image after size filtering (T = 10)

How to get the position and angle of robot n n n Get frame-grabber, color CCD camera and computer. Understand how you can read the image data from framegrabber. Find the position of a colored object in 2 -D image. Determine the robot uniform with two colored objects Calculate the position and angle of the robot from the positions of two colored objects.
![Position of colored object 1. Setting of ranges for YUV - [Ymin, Ymax], [Umin, Position of colored object 1. Setting of ranges for YUV - [Ymin, Ymax], [Umin,](http://slidetodoc.com/presentation_image_h/ceb74a08dcff5af70b061ce097351cbd/image-25.jpg)
Position of colored object 1. Setting of ranges for YUV - [Ymin, Ymax], [Umin, Umax], [Vmin, Vmax] 2. Thresholding 3. Labeling (grouping) 4. Size filtering (noise elimination) 5. Finding the center of a colored object
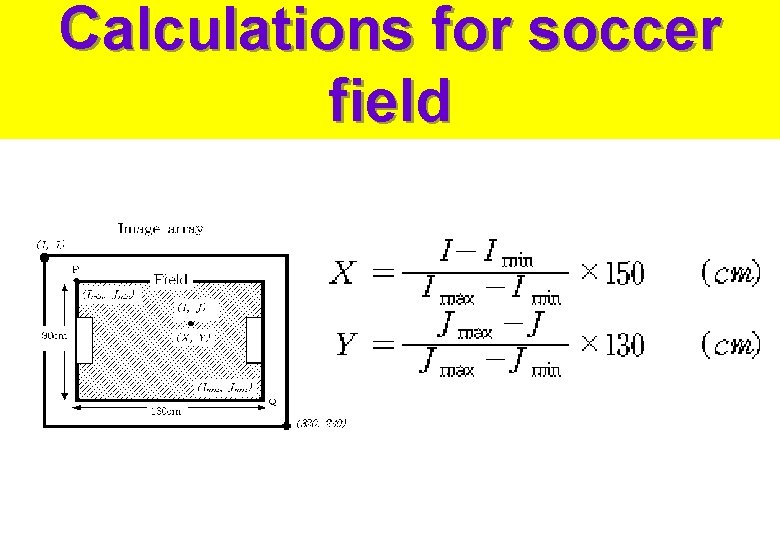
Calculations for soccer field
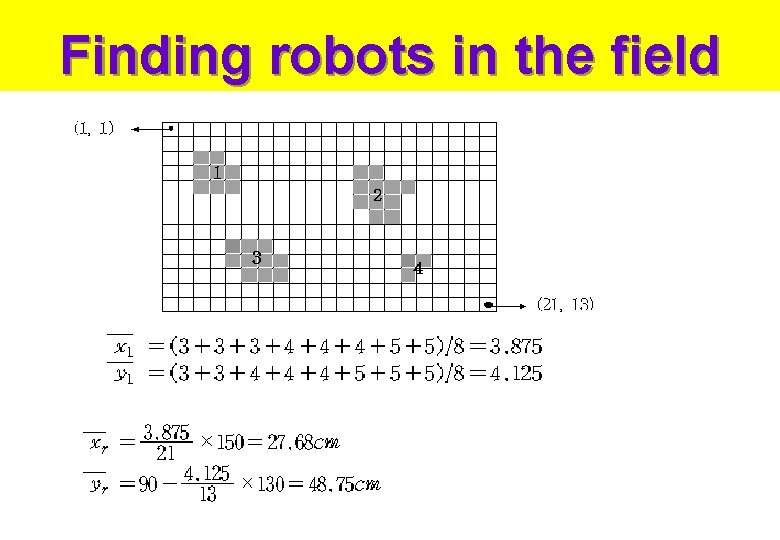
Finding robots in the field
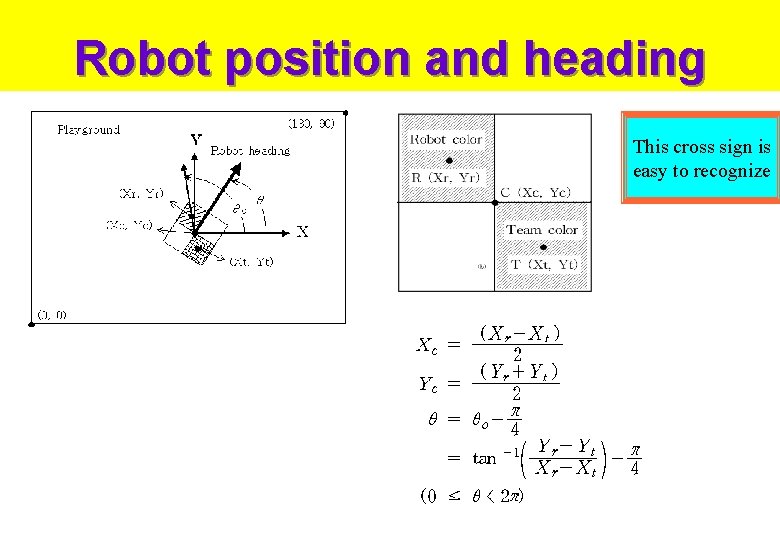
Robot position and heading This cross sign is easy to recognize
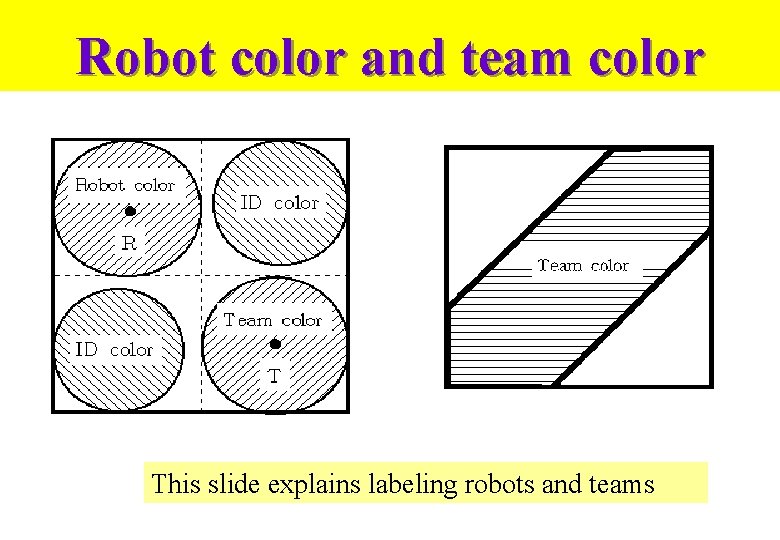
Robot color and team color This slide explains labeling robots and teams
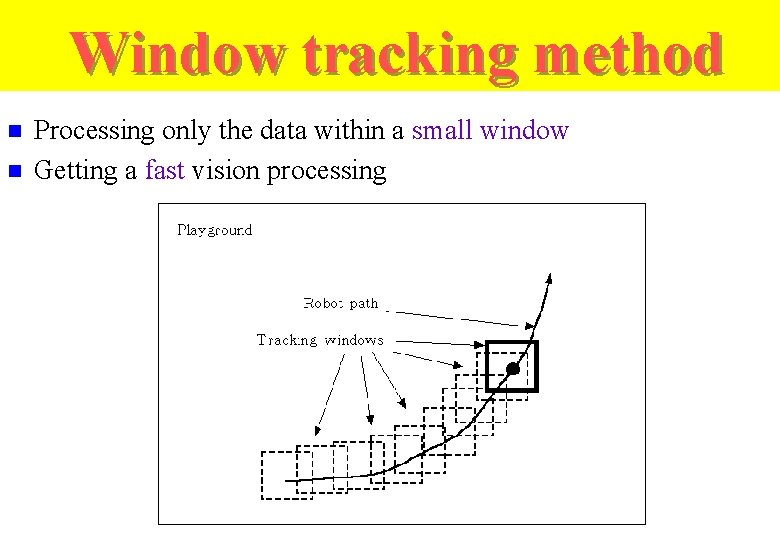
Window tracking method n n Processing only the data within a small window Getting a fast vision processing
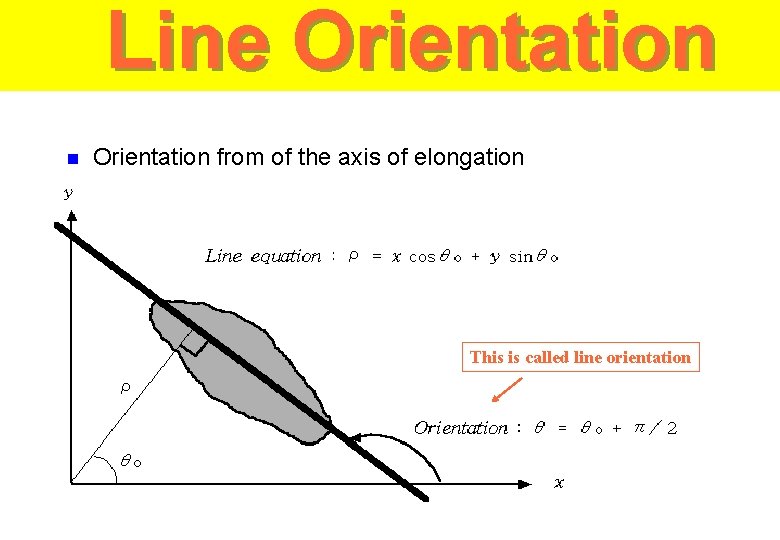
Line Orientation n Orientation from of the axis of elongation This is called line orientation

l Line equation - l : : the minimum distance between the line and origin : the angle from x-axis to the line The distance, d, from any (x, y) within the object to the line : - which satisfies l Minimize Our task is to find values of angle theta and rho for which this formula is minimum. This provides best fit to line equation

Given is object. Find its line orientation l l The center of object : Let 1. Calculate center 2. Calculate a, b, and c.
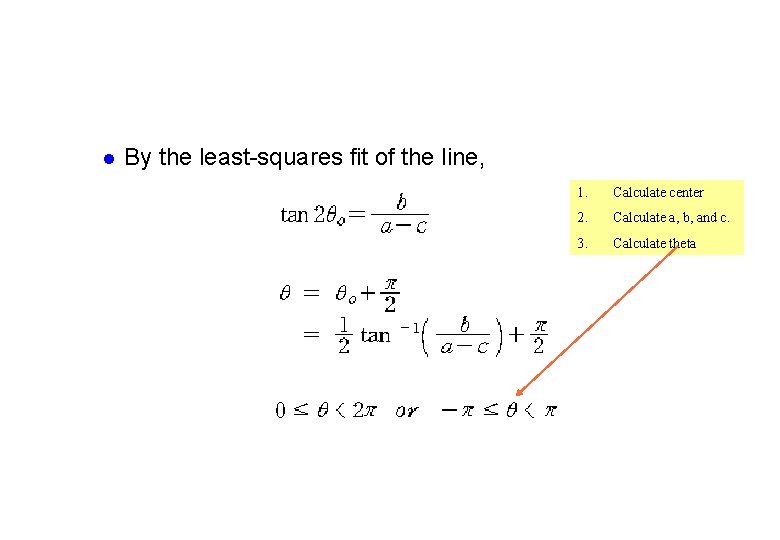
l By the least-squares fit of the line, 1. Calculate center 2. Calculate a, b, and c. 3. Calculate theta

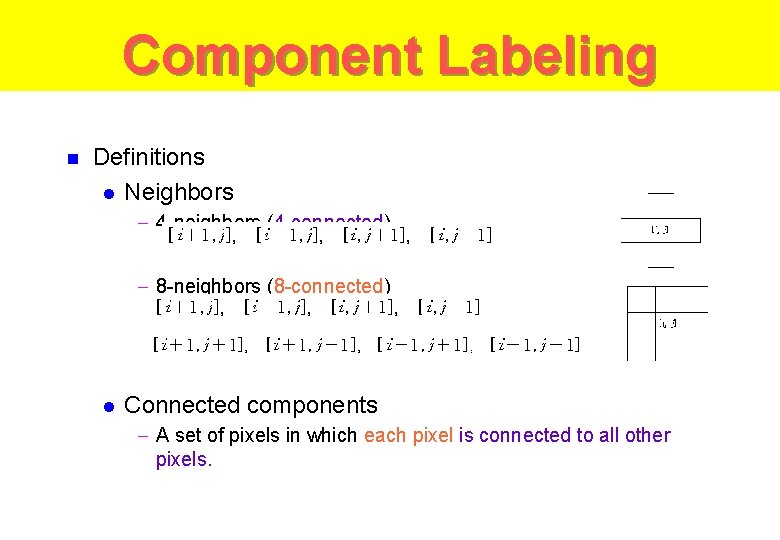
Binary algorithms n Several definitions l Neighbors - 4 -neighbors (4 -connected) - 8 -neighbors (8 -connected)

l Path - A sequence of neighbors l Foreground : - The set of all unity valued pixels in an image l Connectivity - A pixel path from l is said to be connected to if there is a to consisting entirely of pixels of. Connected components - A set of pixels in which each pixel is connected to all other pixels.

Component labeling n n Component labeling algorithm l It finds all connected components in an image and assigns a unique label to all the points in a component. l One of the most common operations in machine vision ; Recursive connected components algorithm ; Sequential connected components algorithm The points in a connected component form a candidate region for an object.
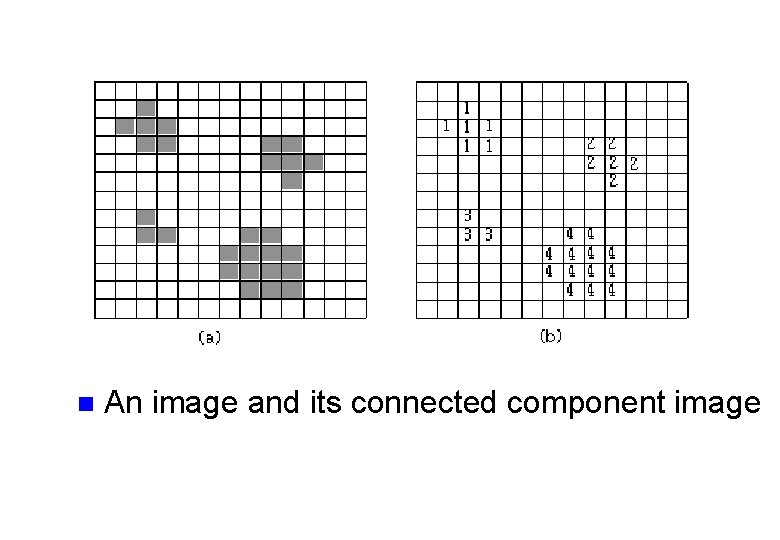
n An image and its connected component image

Recursive algorithm for connected component labeling n Recursive connected components algorithm 1. Scan the image to find an unlabeled unity valued pixel and assign it a new label L. 2. Recursively assign a label L to all its unity valued neighbors. 3. Stop if there are no more unlabeled unity valued pixels. 4. Go to step 1.

n Pseudo code for the recursive algorithm

Sequential algorithm for connected component labeling n Sequential connected components algorithm using 4 -connectivity 1. Scan the image from left to right and top to bottom. 2. If the pixel is unity valued , then (a) If only one of its upper or left neighbors has a label, then copy the label. (b) If both have the same label, then copy the same label. (c) If both have different labels, then copy the upper pixel’s label and enter the labels in an equivalence table as equivalent labels.

Sequential algorithm for connected component labeling continued (d) Otherwise assign a new label to this pixel and enter this label in the equivalence table. 3. If there are more pixels to consider, then go to step 2. 4. Find the lowest label for each equivalent set in the equivalence table. 5. Scan the picture. Replace each label by the lowest label in its equivalent set.

Pseudo code for step 2 in the sequential algorithm
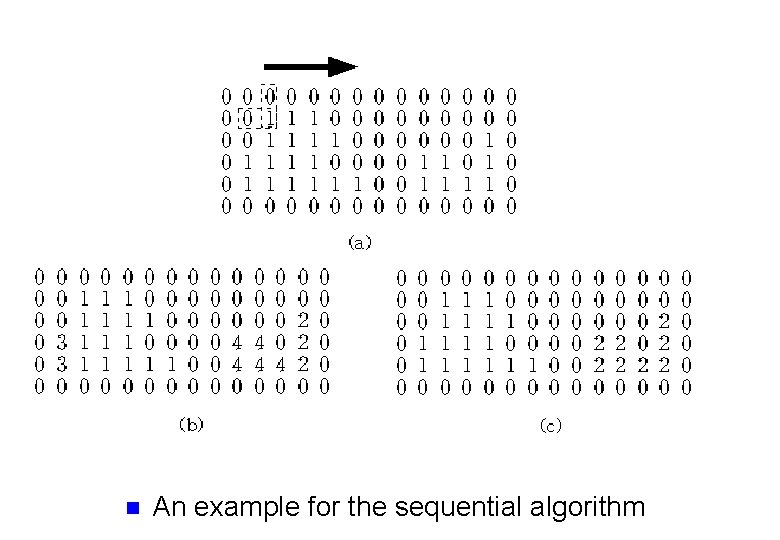
n An example for the sequential algorithm
Digital Geometry I(i, j) (0, 0) j Picture Element or Pixel i 32 Neighborhood n Connectedness n Distance Metrics n Pixel value I(I, j) = 0, 1 Binary Image 0 - K-1 Gray Scale Image Vector: Multispectral Image
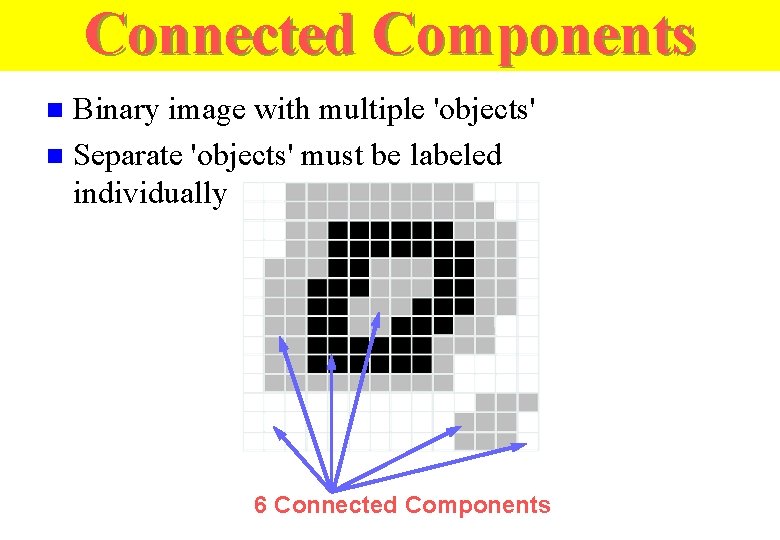
Connected Components Binary image with multiple 'objects' n Separate 'objects' must be labeled individually n 6 Connected Components
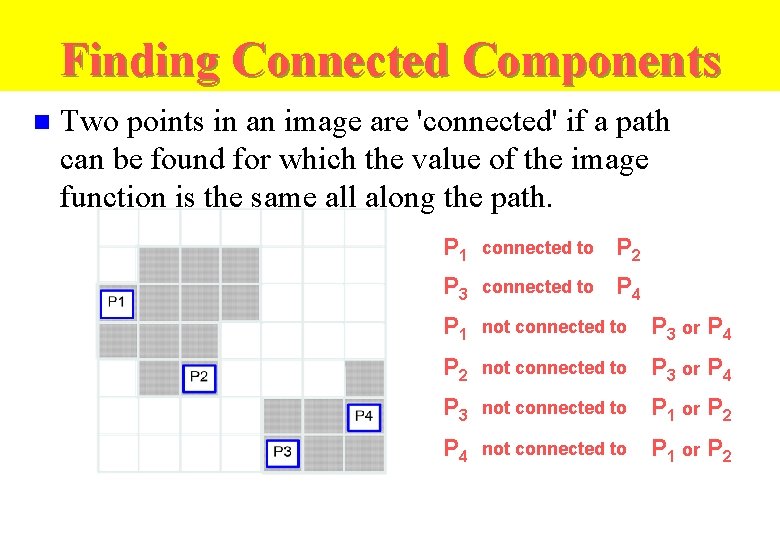
Finding Connected Components n Two points in an image are 'connected' if a path can be found for which the value of the image function is the same all along the path. P 1 connected to P 2 P 3 connected to P 4 P 1 not connected to P 3 or P 4 P 2 not connected to P 3 or P 4 P 3 not connected to P 1 or P 2 P 4 not connected to P 1 or P 2

Algorithm Pick any pixel in the image and assign it a label n Assign same label to any neighbor pixel with the same value of the image function n Continue labeling neighbors until no neighbors can be assigned this label n Choose another label and another pixel not already labeled and continue n If no more unlabeled image points, stop. n Who's my neighbor?

Example
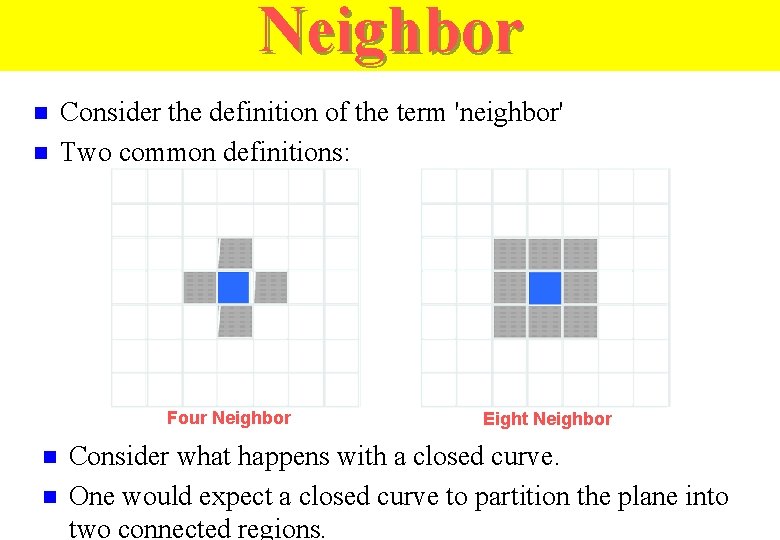
Neighbor n n Consider the definition of the term 'neighbor' Two common definitions: Four Neighbor n n Eight Neighbor Consider what happens with a closed curve. One would expect a closed curve to partition the plane into two connected regions.
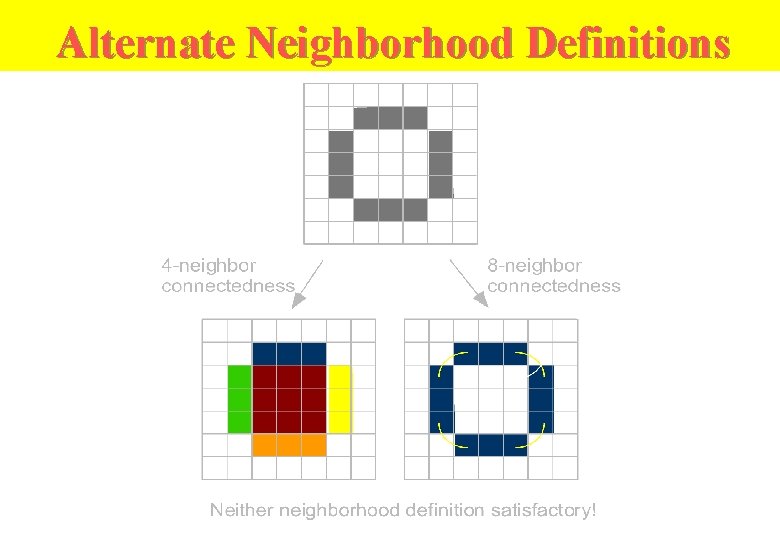
Alternate Neighborhood Definitions
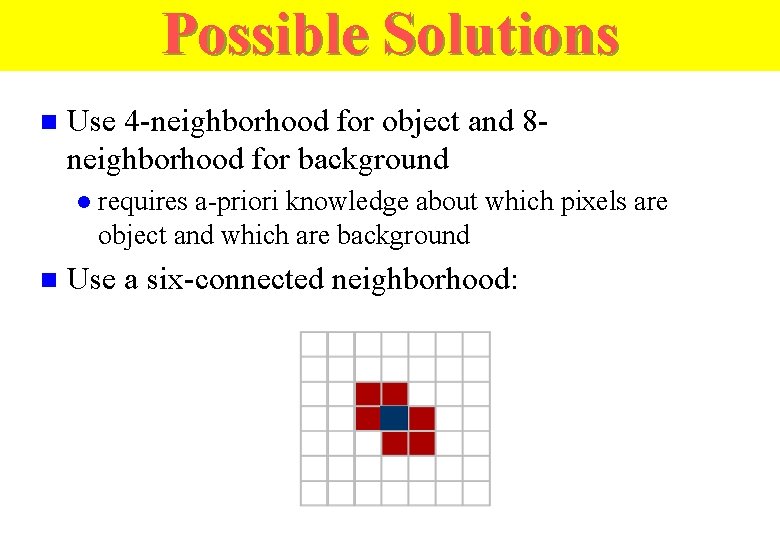
Possible Solutions n Use 4 -neighborhood for object and 8 neighborhood for background l n requires a-priori knowledge about which pixels are object and which are background Use a six-connected neighborhood:
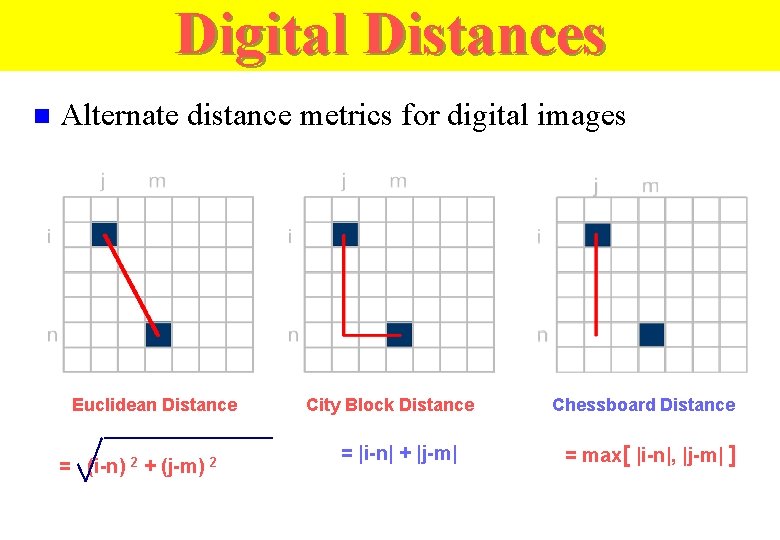
Digital Distances n Alternate distance metrics for digital images Euclidean Distance = (i-n) 2 + (j-m) 2 City Block Distance = |i-n| + |j-m| Chessboard Distance = max[ |i-n|, |j-m| ]

Connected Components / Image Labeling Goal: To find clusters of pixels that are similar and connected to each other n How it works: n Assign a value to each pixel l Define what similar values mean l - e. g. , 10 +/- 2 l Determine if like pixels are connected

Connected Components / Image Labeling 4 - connected 8 -connected
Component Labeling n Definitions l Neighbors - 4 -neighbors (4 -connected) - 8 -neighbors (8 -connected) l Connected components - A set of pixels in which each pixel is connected to all other pixels.

An image and its connected component image
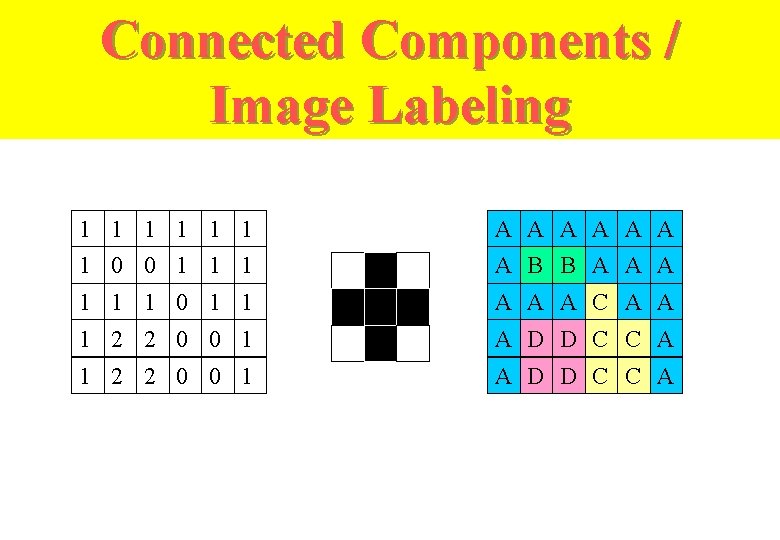
Connected Components / Image Labeling 1 1 1 A A A 1 0 0 1 1 1 A B B A A A 1 1 1 0 1 1 A A A C A A 1 2 2 0 0 1 A D D C C A
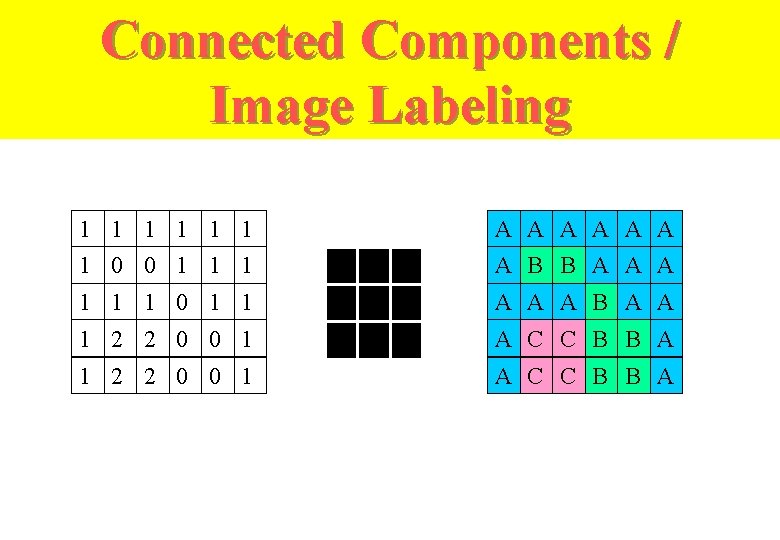
Connected Components / Image Labeling 1 1 1 A A A 1 0 0 1 1 1 A B B A A A 1 1 1 0 1 1 A A A B A A 1 2 2 0 0 1 A C C B B A

Binary Image Processing After thresholding an image, we want to know something about the regions found. . . How many objects are in the image? Where are the distinct “object” components? “Cleaning up” a binary image? Recognizing objects through their response to image masks Describing the shape/structure of 2 d objects Pattern
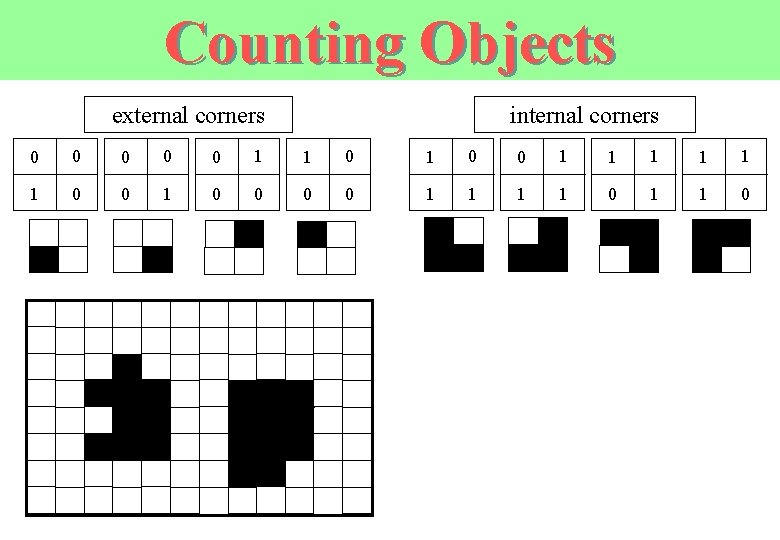
Counting Objects external corners internal corners 0 0 0 1 1 1 0 0 1 1 0
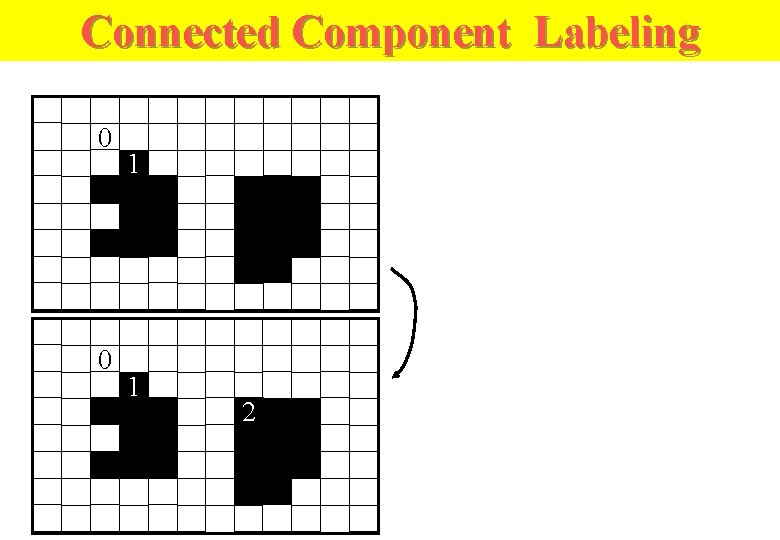
Connected Component Labeling 0 0 1 1 2
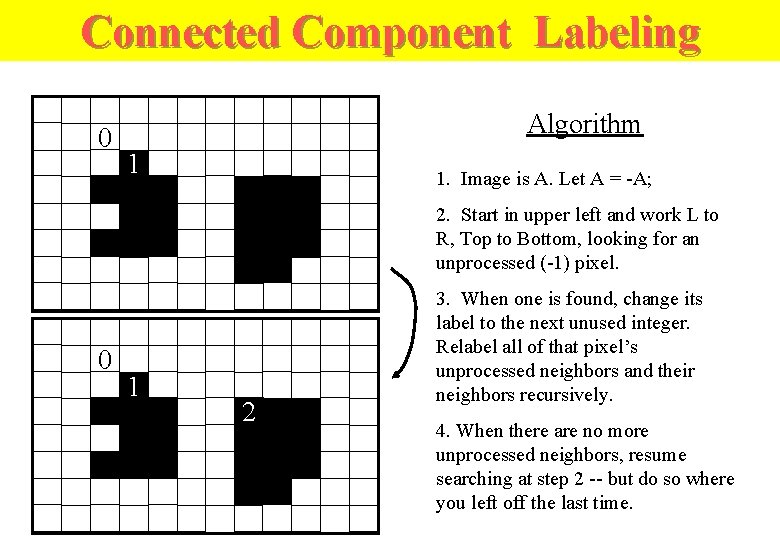
Connected Component Labeling 0 Algorithm 1 1. Image is A. Let A = -A; 2. Start in upper left and work L to R, Top to Bottom, looking for an unprocessed (-1) pixel. 0 1 2 3. When one is found, change its label to the next unused integer. Relabel all of that pixel’s unprocessed neighbors and their neighbors recursively. 4. When there are no more unprocessed neighbors, resume searching at step 2 -- but do so where you left off the last time.

Summary n n A simple procedure to get robot position and heading: l Thresholding, l labeling, l size filtering, l center of area calculation, l window tracking method Trade-off between: l l n real-time vision processing and robustness Specific frame grabber required

Problems for students 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. Binary image processing and basic operations on binary images. List and explain briefly operations used in image enhancement What are point operations. Give examples. Explain contrast stretching operation. Write simple program. Definition of image segmentation. Segmentation based on thresholding Types of thresholding. Give examples of each with practical applications. The general idea of histogram equalization. Show examples. Geometric positions of objects in robot soccer. Size and position of objects in robot soccer.

Problems for students 11. How to calculate quickly the center of the mass of an object? 12. How to calculate line orientation? 13. Describe and program size filter for noise removal. Emphasize speed not quality. 14. How to calculate position and angle of a robot using the ceiling camera? 15. Use of colors in vision of robot soccer. 16. Window tracking methods in robot soccer. 17. Use of Line orientation in robot soccer.

Problems for students 18. 19. 20. 21. 22. 23. 24. 25. 26. Binary image processing algorithms in robot soccer. Component labeling Recursive connected components algorithm Sequential connected components algorithm Algorithms to find connected components. Alternate definitions of neighbors in connected components algorithms. Applications in robot soccer. The concept of digital distance and its use. Connected component labeling in binary images. Counting objects. What are applications in robot soccer?
- Slides: 67