Objective 1 To simplify a rational expression Objective

• Objective 1: To simplify a rational expression. • Objective 2: To multiply rational expressions. • Objective 3: To divide rational expressions

OBJECTIVE 1: TO SIMPLIFY A RATIONAL EXPRESSION

RATIONAL EXPRESSION A fraction in which the numerator and denominator are polynomials is called a rational expression.

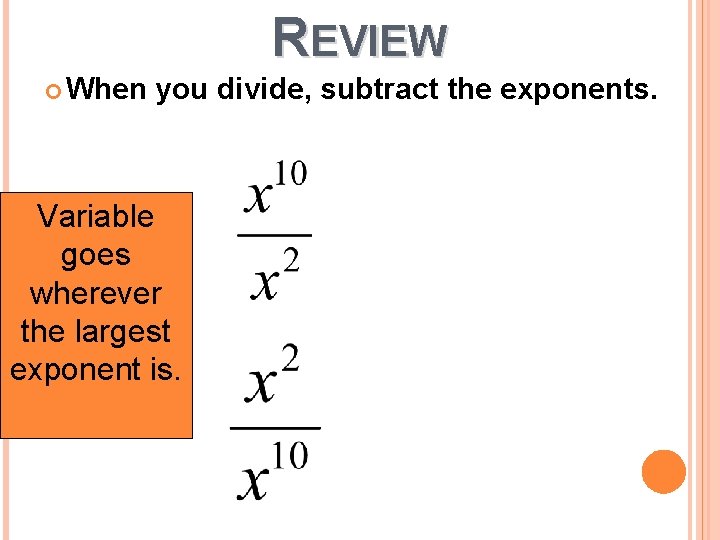
REVIEW When you divide, subtract the exponents. Variable goes wherever the largest exponent is.

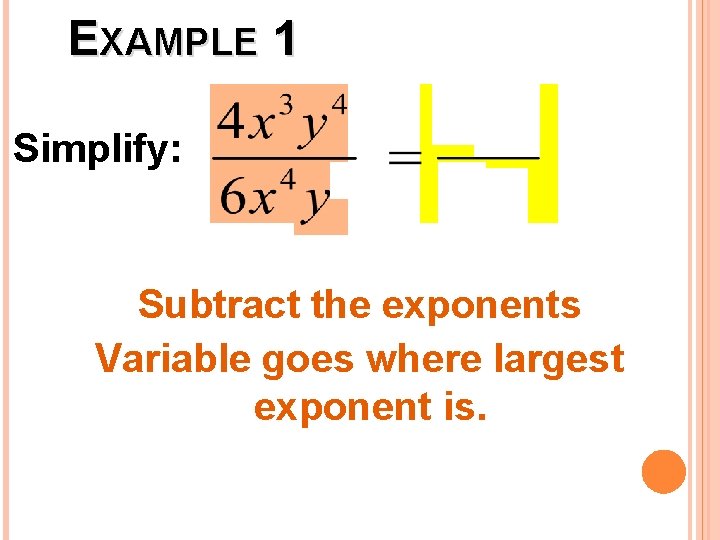
EXAMPLE 1 Simplify: Subtract the exponents Variable goes where largest exponent is.

REVIEW If you have the same binomial on the top and bottom of a fraction, they cancel to 1. 1 1

EXAMPLE 3 Simplify: NO! You can’t cancel with + and – signs.

EXAMPLE 3 Simplify: We need to FACTOR FIRST then cancel.

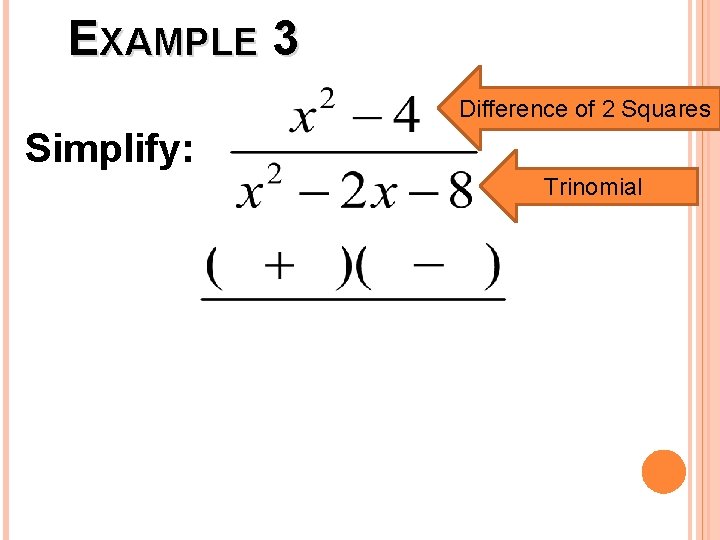
EXAMPLE 3 Difference of 2 Squares Simplify: Trinomial

EXAMPLE 3 Simplify:

EXAMPLE 4 Simplify: We rewrite the numerator in standard form.

EXAMPLE 4 Simplify: Trinomial Factor out – 1 so the leading coefficient will be 1.

EXAMPLE 4 Simplify: Trinomial

Trinomial Put negative sign outside fraction.

REVIEW You can change the order of subtraction, if you factor out a negative one.

EXAMPLE 5 Simplify: Factor out – 1 so we will have (x 2 – 9) in the numerator.

EXAMPLE 5 Simplify: Difference of 2 Squares Trinomial

EXAMPLE 5

EXAMPLE 7 Simplify: 1 1

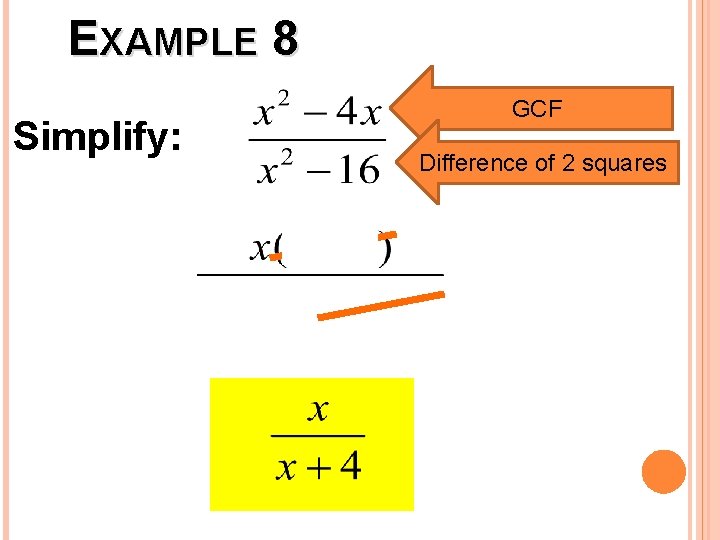
EXAMPLE 8 Simplify: GCF Difference of 2 squares

EXAMPLE 9 Simplify: Trinomial There is a number in front. Factor by grouping. Do this neatly on scratch paper.

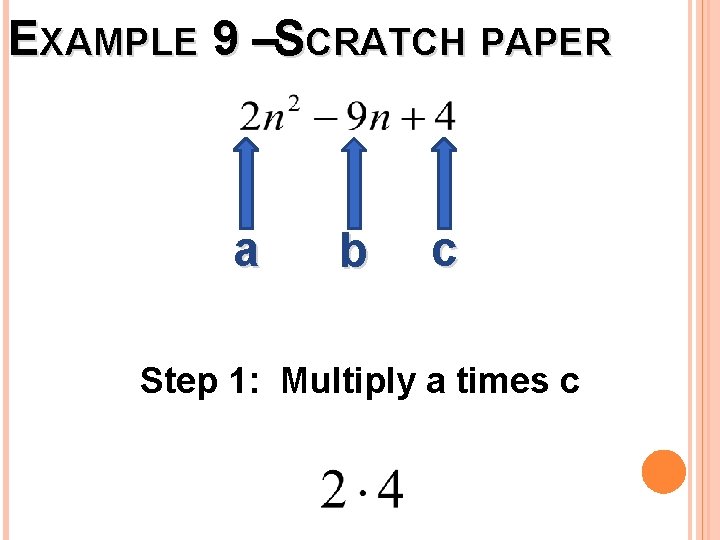
EXAMPLE 9 –SCRATCH PAPER a b c Step 1: Multiply a times c

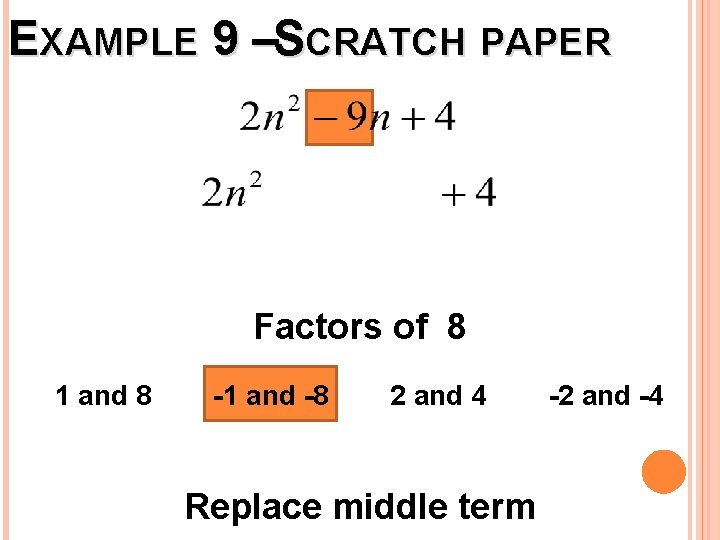
EXAMPLE 9 –SCRATCH PAPER Factors of 8 1 and 8 -1 and -8 2 and 4 Replace middle term -2 and -4

EXAMPLE 9 –SCRATCH PAPER Go back to the problem

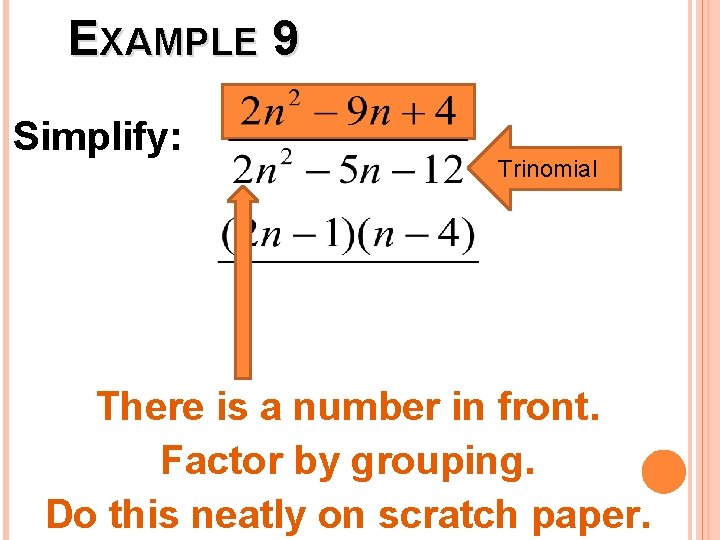
EXAMPLE 9 Simplify: Trinomial There is a number in front. Factor by grouping. Do this neatly on scratch paper.

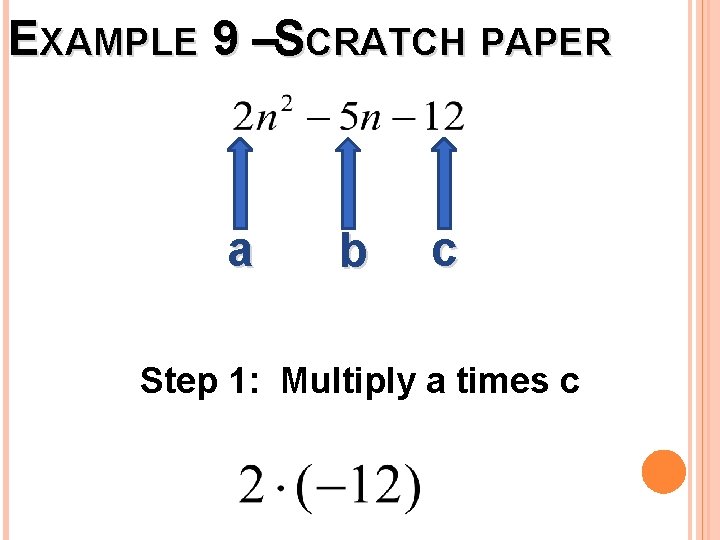
EXAMPLE 9 –SCRATCH PAPER a b c Step 1: Multiply a times c

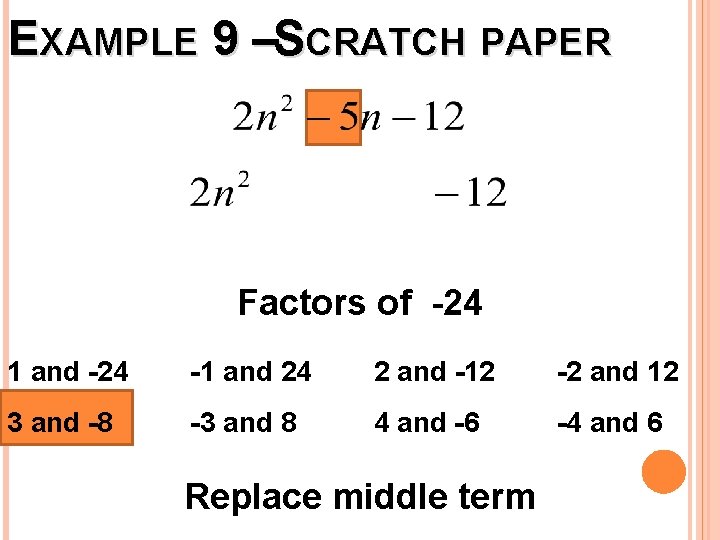
EXAMPLE 9 –SCRATCH PAPER Factors of -24 1 and -24 -1 and 24 2 and -12 -2 and 12 3 and -8 -3 and 8 4 and -6 -4 and 6 Replace middle term

EXAMPLE 9 –SCRATCH PAPER Go back to the problem

EXAMPLE 9 Simplify:

OBJECTIVE 2: TO MULTIPLY RATIONAL EXPRESSIONS

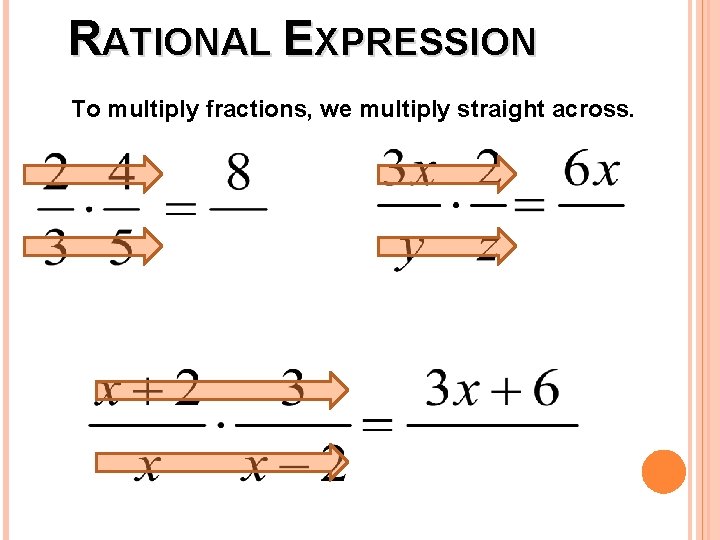
RATIONAL EXPRESSION To multiply fractions, we multiply straight across.

EXAMPLE 10 Multiply: Cancel and Multiply Across

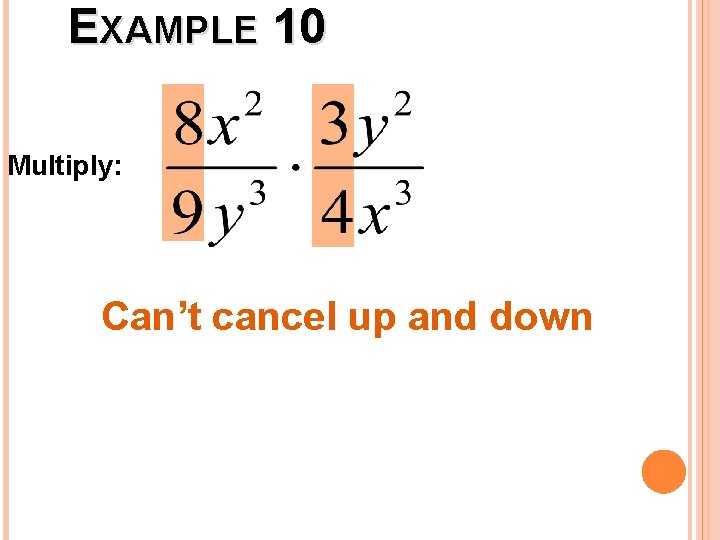
EXAMPLE 10 Multiply: Can’t cancel up and down

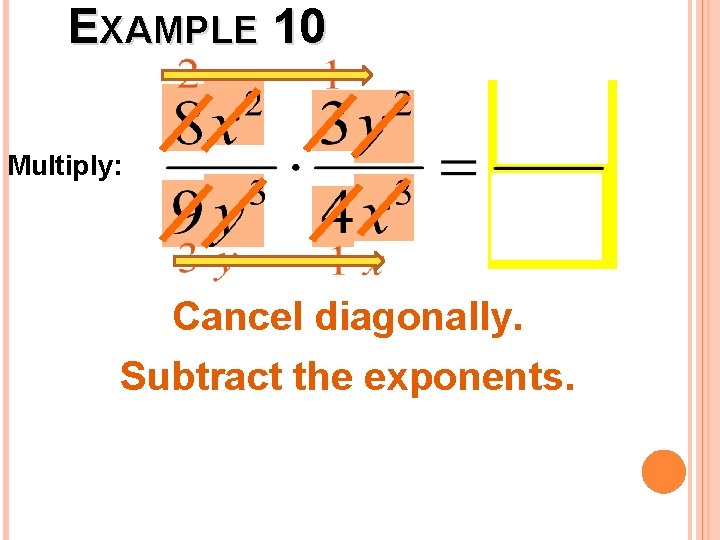
EXAMPLE 10 Multiply: Cancel diagonally. Subtract the exponents.

EXAMPLE 11 Multiply: Factor, Cancel, then Multiply Across.

EXAMPLE 11 Multiply: Factor out the GCF.

EXAMPLE 11 Multiply: Trinomial

EXAMPLE 11 Multiply: Trinomial

EXAMPLE 11 Multiply: Trinomial

EXAMPLE 11 Multiply: Cancel

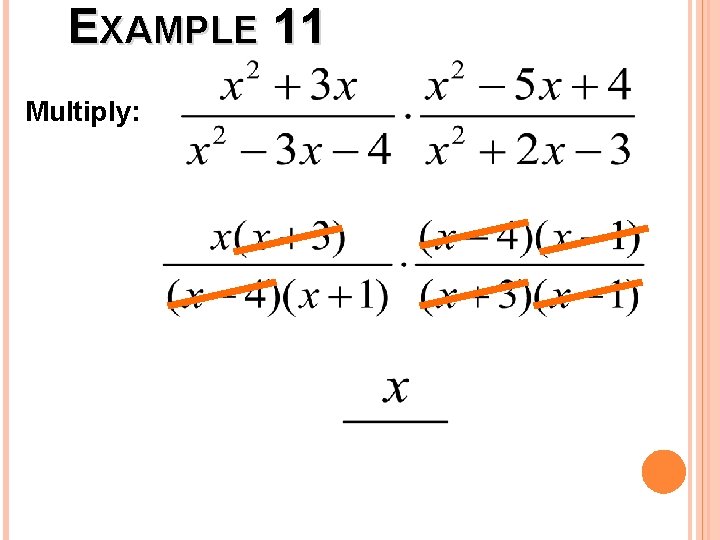
EXAMPLE 11 Multiply:

EXAMPLE 11 Multiply:

OBJECTIVE 3: TO DIVIDE A RATIONAL EXPRESSION

RATIONAL EXPRESSION To divide fractions, remember KFC. eep the first fraction. lip the second fraction. RECIPROCAL hange to multiplication.

RATIONAL EXPRESSION To divide fractions, remember KFC.

EXAMPLE 14 Divide: Perform KFC.

EXAMPLE 14 Divide: Factor out GCF.

EXAMPLE 14 Divide: Cannot Factor.

EXAMPLE 14 Divide: Cannot Factor.

EXAMPLE 14 Divide: Factor out GCF.

EXAMPLE 14 Divide: Factor out -1

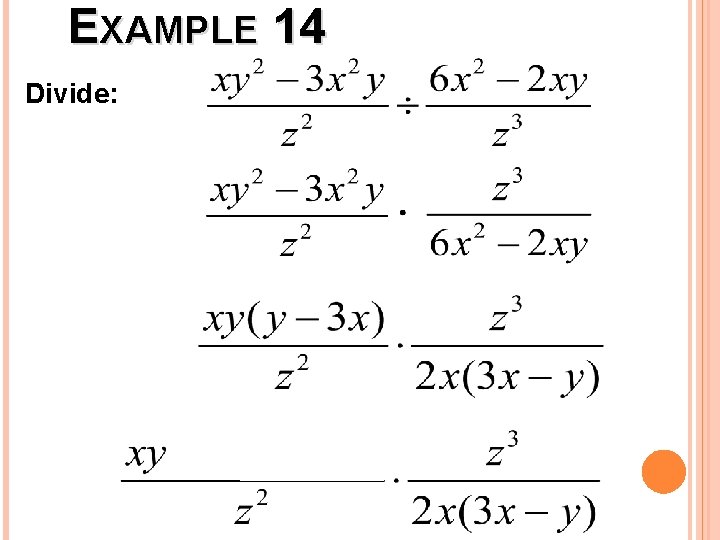
EXAMPLE 14 Divide:

EXAMPLE 14 Cancel