Object Intersection CSE 681 Object Representation Implicit forms

Object Intersection CSE 681

Object Representation Implicit forms F(x, y, z) = 0 testing Explicit forms Analytic form x = F(y, z) Parametric form (x, y, z) = P(t) CSE 681 generating

Ray-Object Intersection Implicit forms F(x, y, z) = 0 Ray: P(t) = (x, y, z) = source + t*direction = s + t*v Solve for t: F(P(t)) = 0 CSE 681

Ray-Sphere Intersection Implicit form for sphere at origin of radius 1 Ray: Solve: … Use quadratic equation… CSE 681

Ray-Sphere Intersection At 2 + Bt + C = 0 A = |v|2 B = 2 s·v C = |s|2 - 1 B 2 -4 AC < 0 => no intersection = 0 => just grazes > 0 => two hits CSE 681

Axis-Aligned Cuboid (rectangular solid, rectangular parallelpiped) Ray equation Planar equations P(t) = s + tv Y = y 2 Solve for intersections with planes tx 1 = (x 1 - sx)/vx Z = z 2 tx 2 = (x 2 - sx)/vx X = x 1 Z = z 1 ty 1 = (y 1 - sx)/vx Y = y 1 … CSE 681 X = x 2

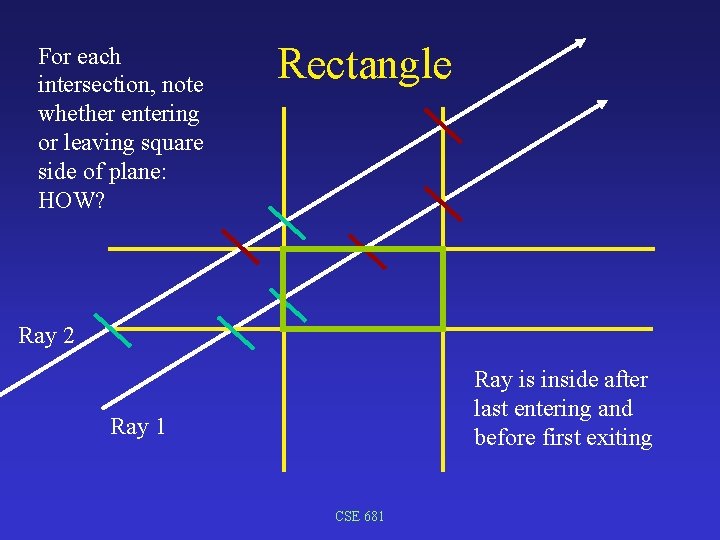
For each intersection, note whether entering or leaving square side of plane: HOW? Rectangle Ray 2 Ray is inside after last entering and before first exiting Ray 1 CSE 681

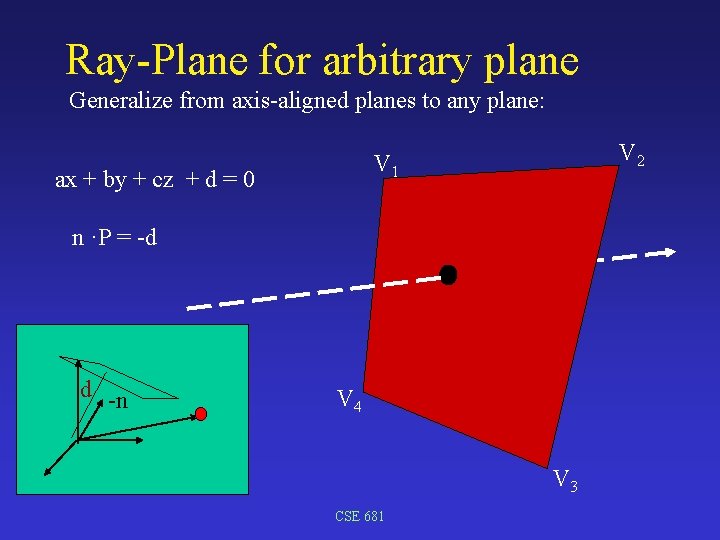
Ray-Plane for arbitrary plane Generalize from axis-aligned planes to any plane: V 2 V 1 ax + by + cz + d = 0 n ·P = -d d -n V 4 V 3 CSE 681

Normal Vector Given ordered sequence of points defining a polygon how do you find a normal vector for the plane? Note: 2 normal vectors to a plane, colinear and one is the negation of the other Ordered: e. g. , clockwise when viewed from the front of the face Right hand v. left hand space CSE 681

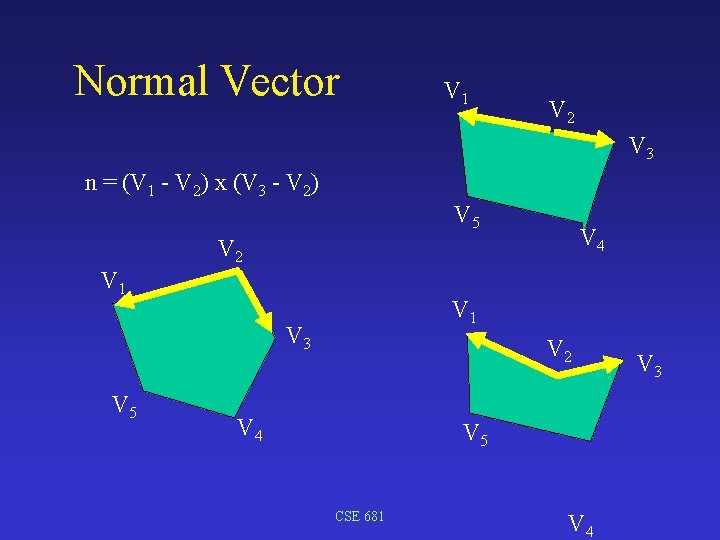
Normal Vector V 1 V 2 V 3 n = (V 1 - V 2) x (V 3 - V 2) V 5 V 4 V 2 V 1 V 3 V 5 V 2 V 4 V 5 CSE 681 V 4 V 3

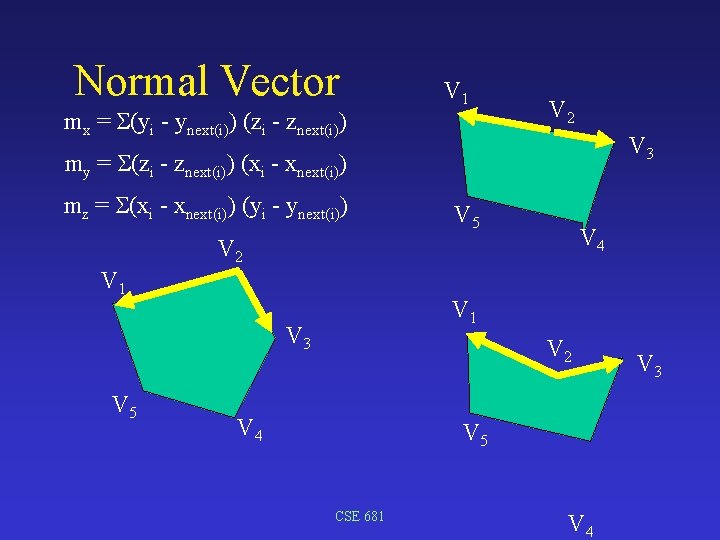
Normal Vector mx = S(yi - ynext(i)) (zi - znext(i)) V 1 V 2 V 3 my = S(zi - znext(i)) (xi - xnext(i)) mz = S(xi - xnext(i)) (yi - ynext(i)) V 5 V 4 V 2 V 1 V 3 V 5 V 2 V 4 V 5 CSE 681 V 4 V 3

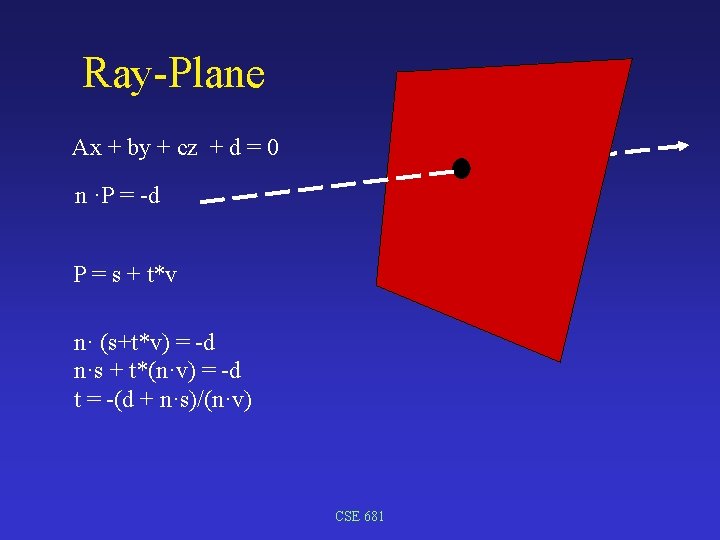
Ray-Plane Ax + by + cz + d = 0 n ·P = -d P = s + t*v n· (s+t*v) = -d n·s + t*(n·v) = -d t = -(d + n·s)/(n·v) CSE 681

Ray-Polyhedron - volume bounded by flat faces Each face is defined by a ring of edges Each edge is shared by 2 and only 2 faces The polyhedron can be convex or concave Faces can be convex or concave CSE 681

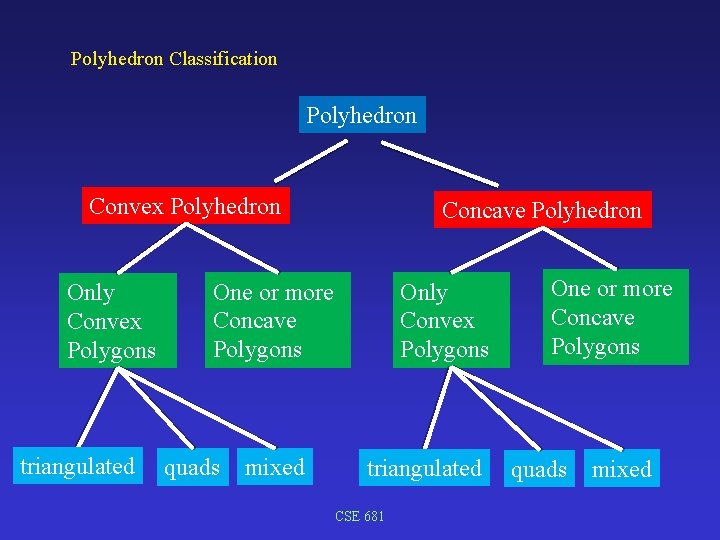
Polyhedron Classification Polyhedron Convex Polyhedron Only Convex Polygons triangulated Concave Polyhedron One or more Concave Polygons quads mixed Only Convex Polygons triangulated CSE 681 One or more Concave Polygons quads mixed

Solid Modeling of three-dimensional solids Physically realizable objects No infinitely thin sheets, no lines Interior of object should ‘hold water’ - Define a closed volume http: //www. gvu. gatech. edu/~jarek/papers/Solid. Modeling. Webster. pdf CSE 681

Polygonal Solid Models Vertices of a face have a consistent ordering (e. g. clockwise) when viewed from the outside of the face Each edge of a face is shared by one and only one other face Each edge appears oriented one way in one face and the other way in the other face EULER’S FORMULA F–E+V=2 F – E + V = 2 – 2 P CSE 681

Convex Polyhedron volume bounded by finite number of infinite planes Computing intersections is similar to cube but using ray -plane intersection and arbitrary number of planes n· P= -d P(t) = s + t*v Use n· v to determine Entering/exiting status n· (s+t*v) = -d n·s + t*(n·v) = -d t = -(d + n·s)/(n·v) CSE 681

Convex Polyhedron Intersection going from outside to inside Intersection going from inside to outside Record maximum entering intersection - enter. Max Record minimum exiting intersection - exit. Min If (enter. Max < exit. Min) polyhedron is intersected CSE 681

Concave Polyhedron Find closest face (if any) intersected by ray Need ray-face (ray-polygon) intersection test CSE 681

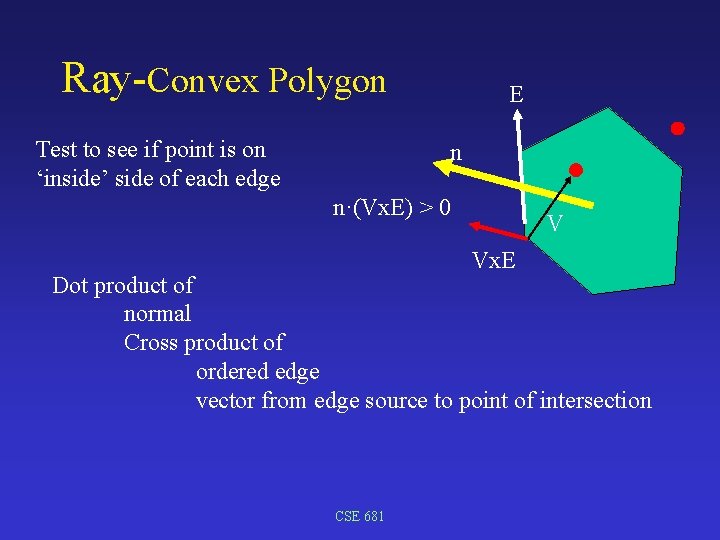
Ray-Convex Polygon Test to see if point is on ‘inside’ side of each edge E n n·(Vx. E) > 0 V Vx. E Dot product of normal Cross product of ordered edge vector from edge source to point of intersection CSE 681

Ray-Concave Polyhedron 1. Intersect ray with plane 2. Determine if intersection point is inside of 2 D polygon A) Convex polygon B) Concave polygon CSE 681

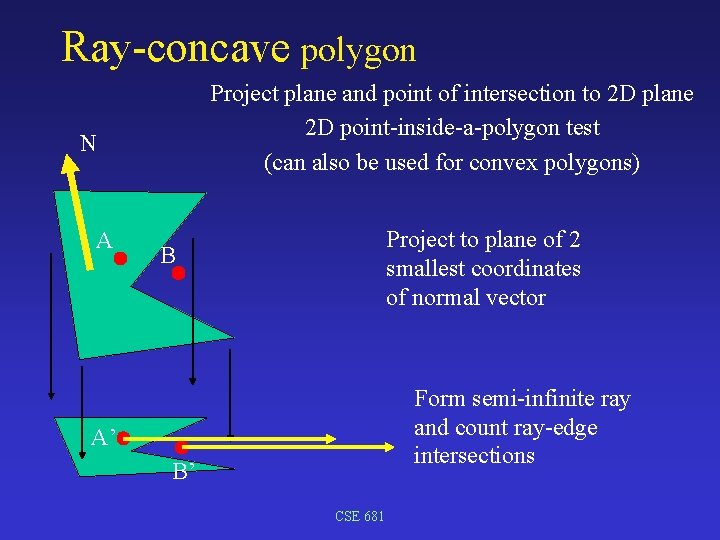
Ray-concave polygon Project plane and point of intersection to 2 D plane 2 D point-inside-a-polygon test (can also be used for convex polygons) N A Project to plane of 2 smallest coordinates of normal vector B Form semi-infinite ray and count ray-edge intersections A’ B’ CSE 681

2 D Point Inside a Convex Polygon p Semi-infinite ray test Test to see if point is on ‘inside’ side of each edge p 2 Need to know order (CW or CCW) of 2 D vertices p 1 CSE 681 p

2 D point inside a polygon test CSE 681

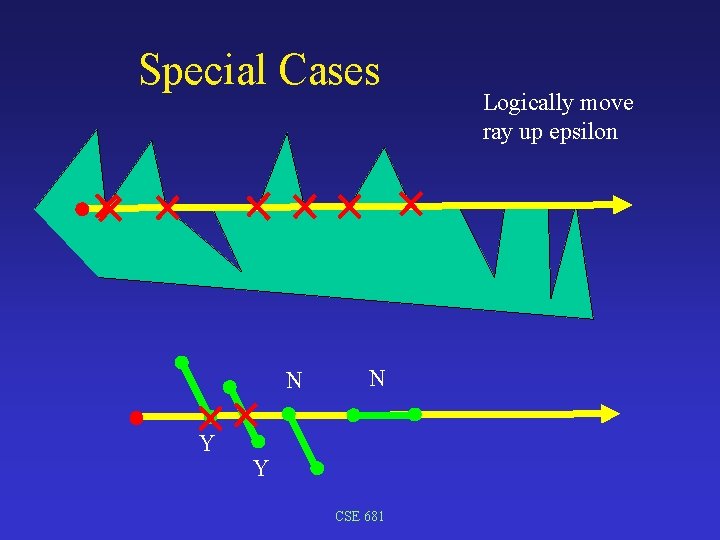
Special Cases N Y CSE 681 Logically move ray up epsilon

2 D point inside a polygon test y CSE 681

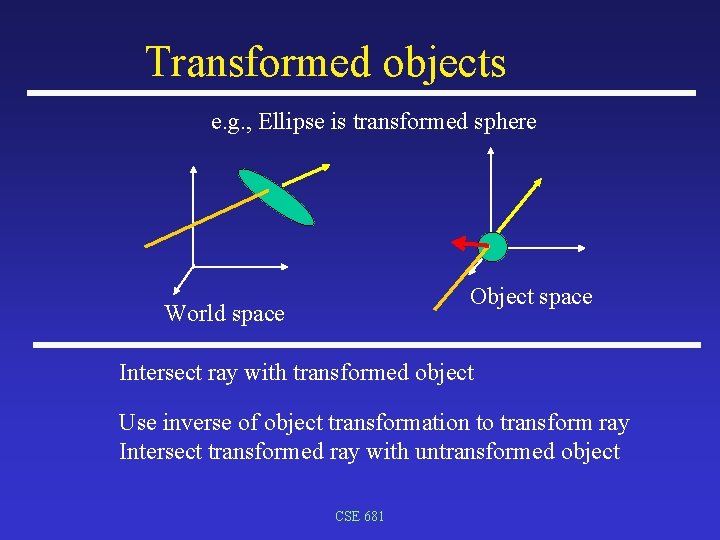
Transformed objects e. g. , Ellipse is transformed sphere Object space World space Intersect ray with transformed object Use inverse of object transformation to transform ray Intersect transformed ray with untransformed object CSE 681

Transformed objects World space ray Object to world transform matrix Object space ray Intersect ray with object in object space Transform intersection point and normal back to world space CSE 681

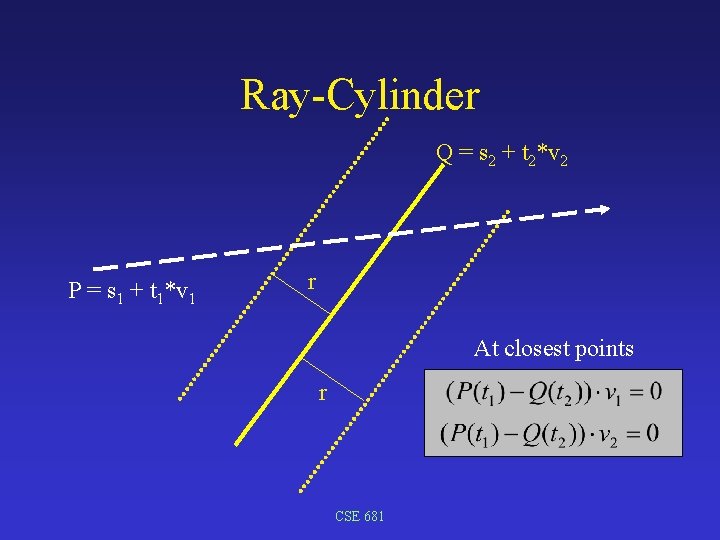
Ray-Cylinder Q = s 2 + t 2*v 2 P = s 1 + t 1*v 1 r At closest points r CSE 681

Ray-Cylinder CSE 681

Ray-Ellipsoid Geometric construction: all points p such that |p-a| + |p-b| = r a b d 1 Algebraic equation – axis aligned, origin centered CSE 681 d 2

Ray-Quadric http: //en. wikipedia. org/wiki/Quadric CSE 681