Object Function for Object Detector Solving Imbalance Problem

Object Function for Object Detector Solving Imbalance Problem 2019/04/01 賴茂睿

Outline ▪ Introduction ▪ Reformulate the cross-entropy loss ▪ Focal Loss for Dense Object Detection ▪ Gradient Harmonized Single-stage Detector

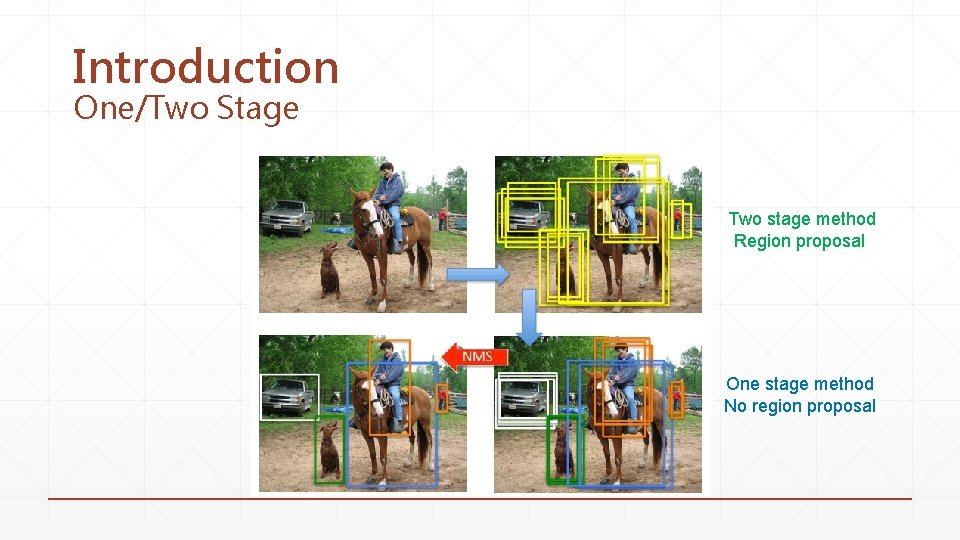
Introduction One/Two Stage Two stage method Region proposal One stage method No region proposal

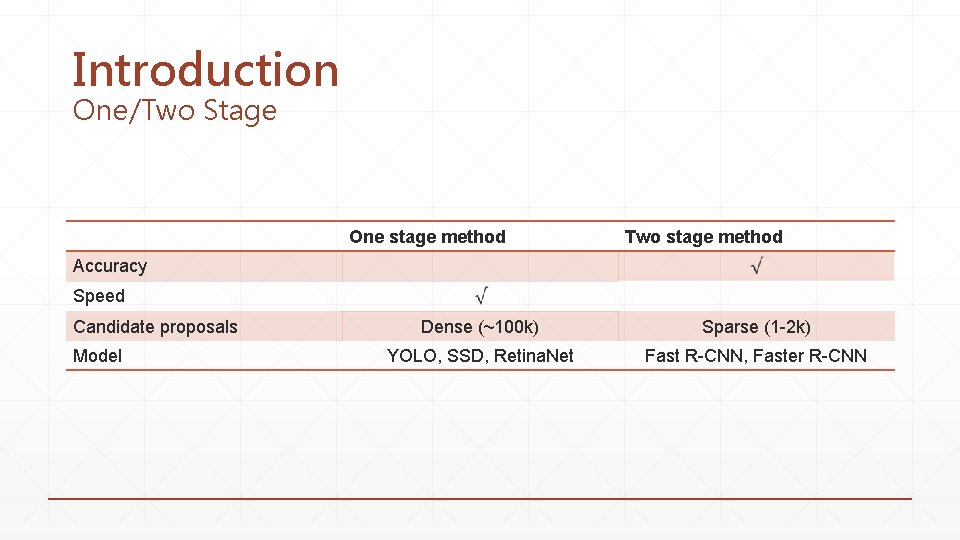
Introduction One/Two Stage One stage method Two stage method Accuracy Speed Candidate proposals Model Dense (~100 k) Sparse (1 -2 k) YOLO, SSD, Retina. Net Fast R-CNN, Faster R-CNN

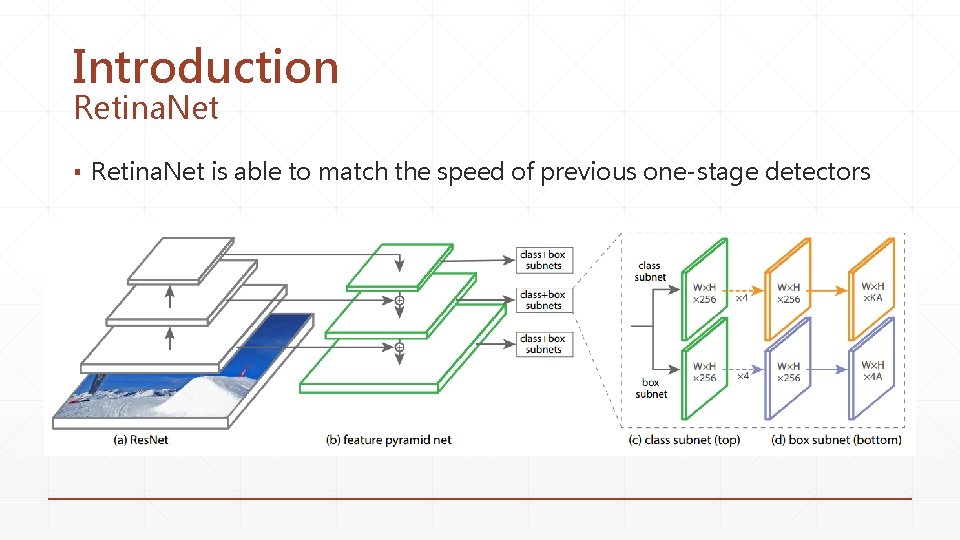
Introduction Retina. Net ▪ Retina. Net is able to match the speed of previous one-stage detectors

Focal Loss for Dense Object Detection Tsung-Yi Lin, Priya Goyal, Ross Girshick, Kaiming He, Piotr Dollar ICCV 2017 (oral)

Viewpoint ▪ Extreme foreground-background class imbalance (1: 1000) ▪ Prevent vast number of easy negatives from overwhelming the detector ▪ Down-weight the loss assigned to well-classified examples ▪ Surpassing the accuracy of all existing state-of-the-art two-stage detectors

Focal Loss ▪ Traditional cross entropy for binary classification

Focal Loss ▪

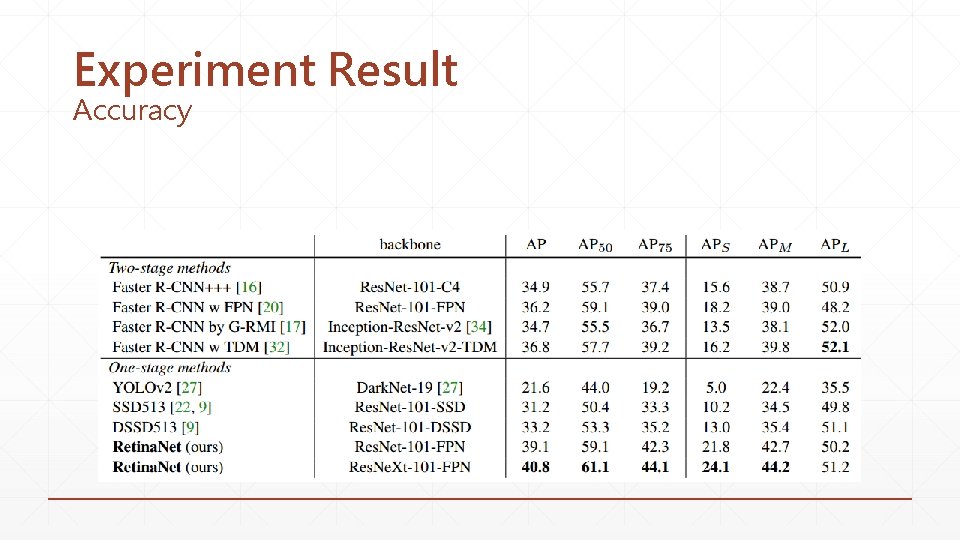
Experiment Result Accuracy

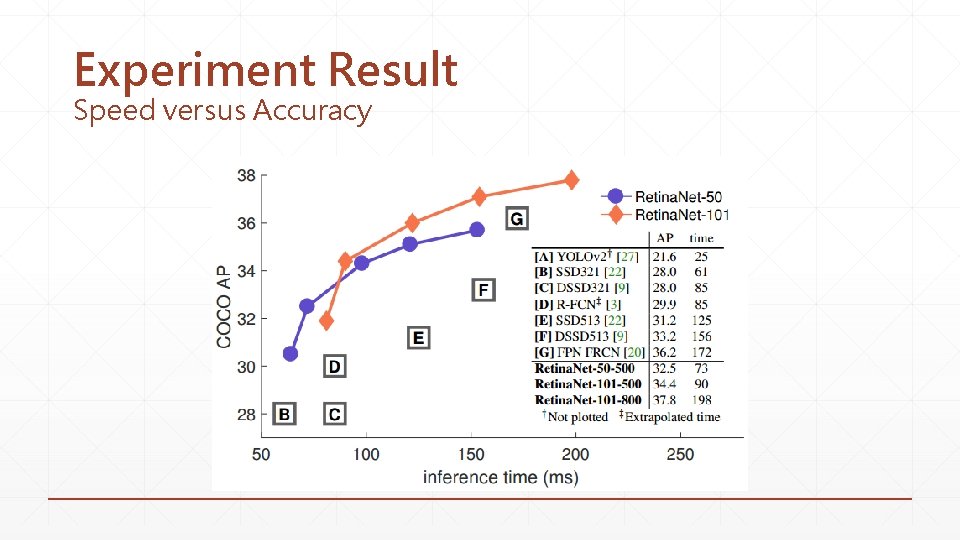
Experiment Result Speed versus Accuracy

Gradient Harmonized Singlestage Detector Buyu Li, Yu Liu, Xiaogang Wang AAAI 2019 (oral)

Viewpoint ▪ Two well-known disharmonies ▪ Huge difference in quantity between positive and negative examples ▪ As well as between easy and hard examples ▪ Distribution of gradient norm ▪ The imbalance of examples with different attributes (hard/easy and pos/neg)

Gradient Norm ▪

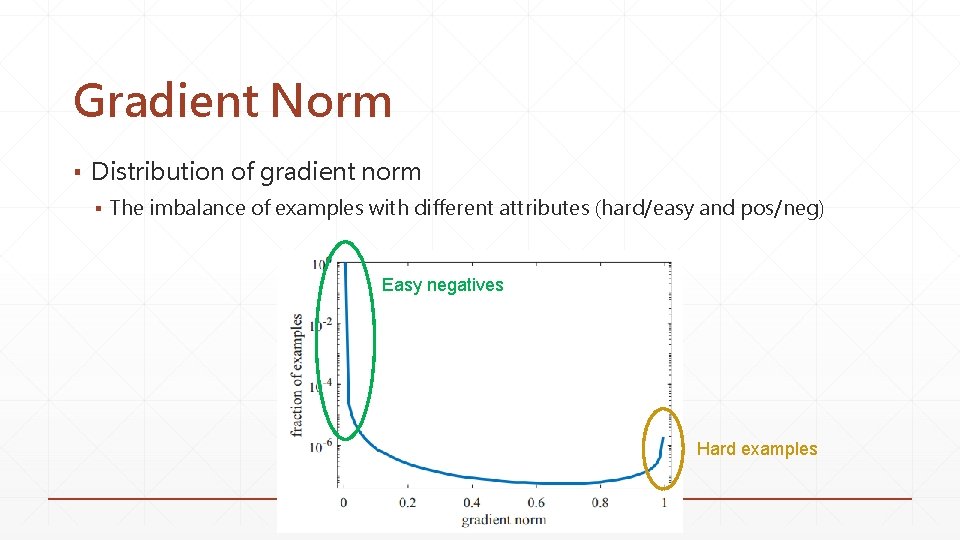
Gradient Norm ▪ Distribution of gradient norm ▪ The imbalance of examples with different attributes (hard/easy and pos/neg) Easy negatives Hard examples

Gradient Norm ▪ Small gradient norm have a large density due to the large amount of easy negative examples ▪ Huge amount of easy examples can overwhelm the contribution of the minority of hard examples and the training process will be inefficient ▪ Outliers (very hard examples) may affect the stability of model

Gradient Density ▪ To handle the problem of the disharmony of gradient norm distribution, we introduce gradient density function

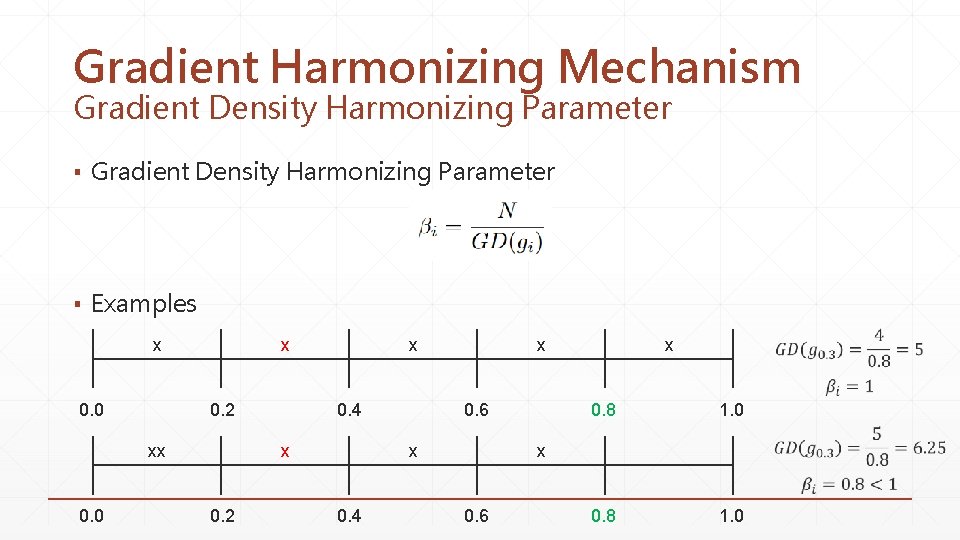
Gradient Harmonizing Mechanism Gradient Density Harmonizing Parameter ▪ Examples x 0. 0 0. 4 0. 2 xx x x 0. 2 x 0. 6 x 0. 4 x 0. 8 1. 0 x 0. 6

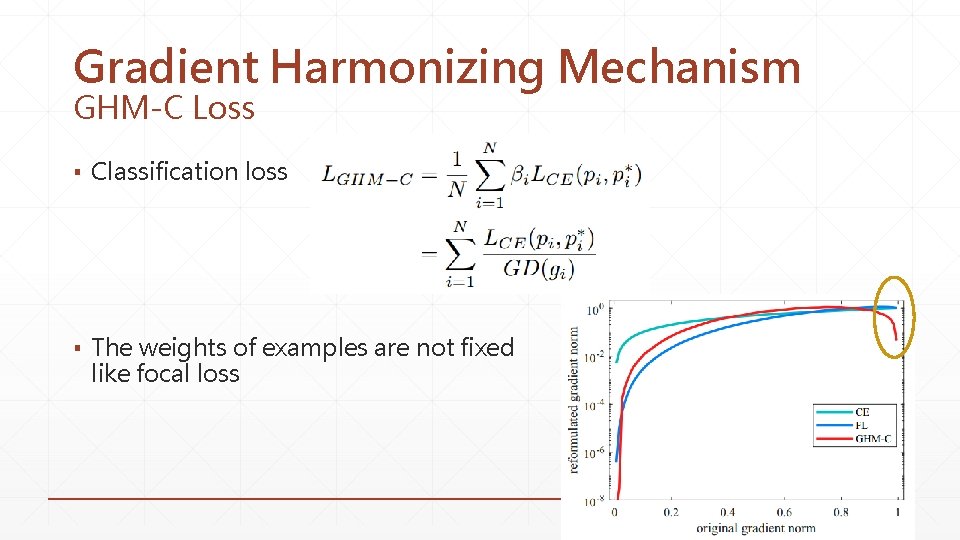
Gradient Harmonizing Mechanism GHM-C Loss ▪ Classification loss ▪ The weights of examples are not fixed like focal loss

Gradient Harmonizing Mechanism GHM-R Loss ▪

Gradient Harmonizing Mechanism GHM-R Loss ▪ Easy example still has deviation from the ground truth location ▪ Better prediction of any example will improve the quality of the final candidates

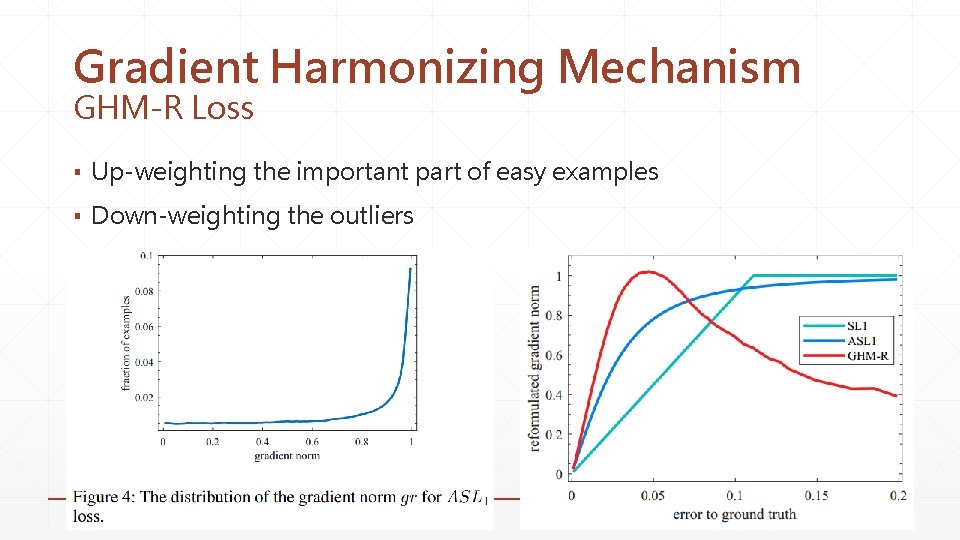
Gradient Harmonizing Mechanism GHM-R Loss ▪ Up-weighting the important part of easy examples ▪ Down-weighting the outliers

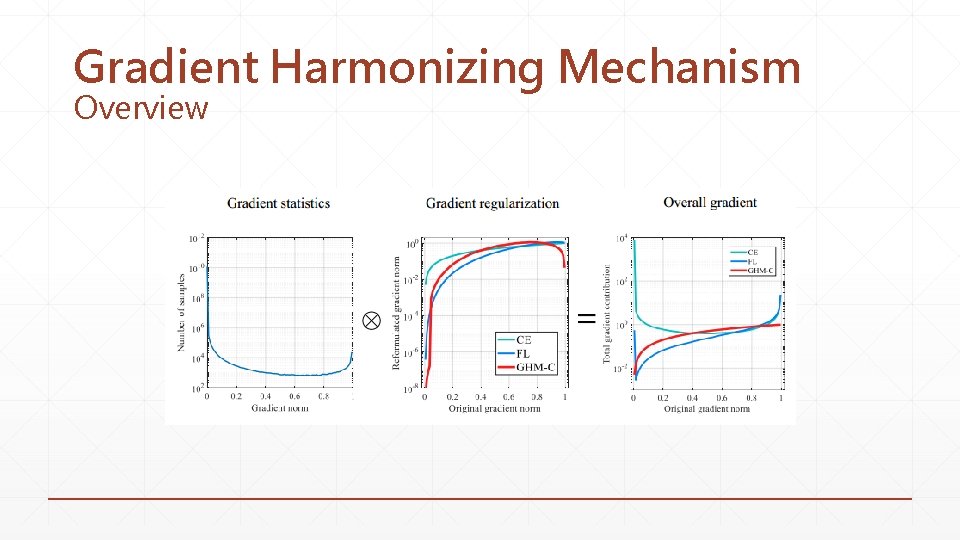
Gradient Harmonizing Mechanism Overview

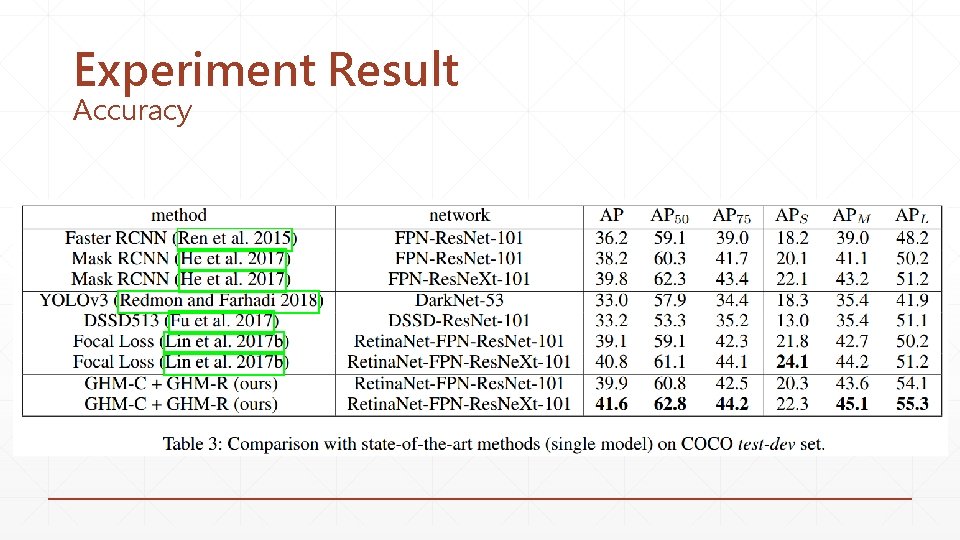
Experiment Result Accuracy

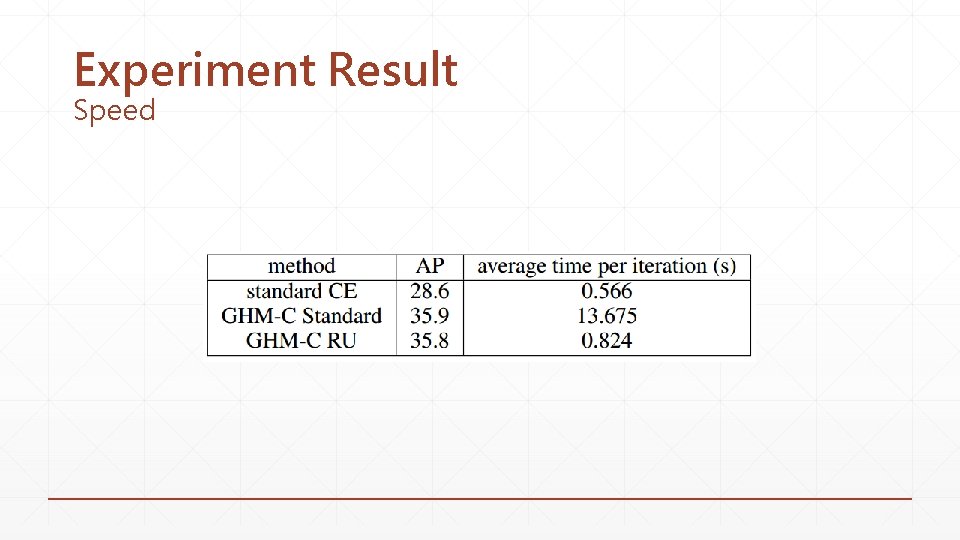
Experiment Result Speed