Obchodn akademie Stedn odborn kola a Jazykov kola

Obchodní akademie, Střední odborná škola a Jazyková škola s právem státní jazykové zkoušky, Hradec Králové Autor: Mgr. Lubomíra Moravcová Název materiálu: VY_32_INOVACE_7_PLANIMETRIE_A_STEREOMETRIE_14 Čtyřúhelníky Téma sady: Planimetrie a stereometrie Obor, ročník: Ekonomické lyceum, Obchodní akademie, Sociální činnost, Veřejnosprávní činnost, 1. – 4. ročník Datum vytvoření: březen 2013 Anotace: Základní rozdělení čtyřúhelníků a jejich popis Metodický obsah: Dělení čtyřúhelníků, jejich základní charakteristika, obvod a obsah

Co je čtyřúhelník • rovinný geometrický útvar • mnohoúhelník se čtyřmi vrcholy a čtyřmi stranami • součet velikostí vnitřních úhlů = 360° (2π) • lze jej úhlopříčkou rozdělit na dva trojúhelníky

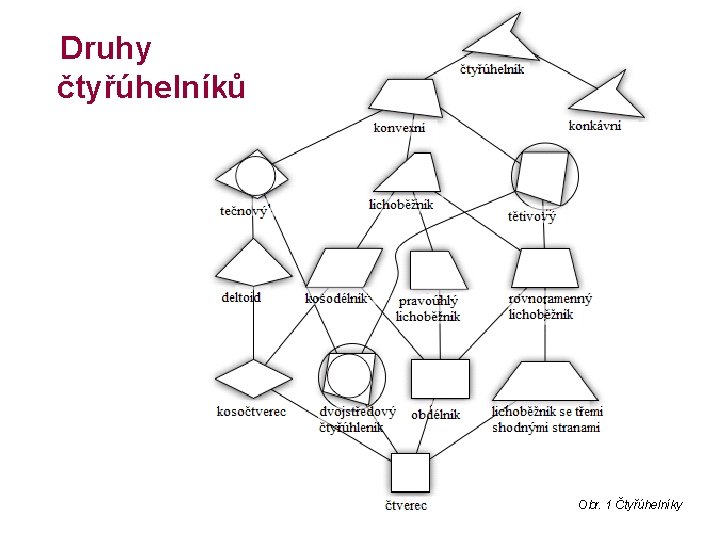
Druhy čtyřúhelníků Obr. 1 Čtyřúhelníky

Dělení čtyřúhelníků Mohou být konvexní (vypuklé) nebo nekonvexní (duté) Konvexní čtyřúhelníky: • různoběžník – žádné dvě protilehlé strany nejsou rovnoběžné • rovnoběžník (kosodélník) – dvě a dvě protilehlé strany jsou rovnoběžné – obdélník – všechny vnitřní úhly jsou pravé – kosočtverec – všechny strany mají stejnou délku – čtverec – všechny strany mají stejnou délku a všechny vnitřní úhly jsou pravé • lichoběžník – jeden pár protilehlých stran je rovnoběžný • deltoid – dvě dvojice vzájemně přiléhajících stran mají stejnou velikost

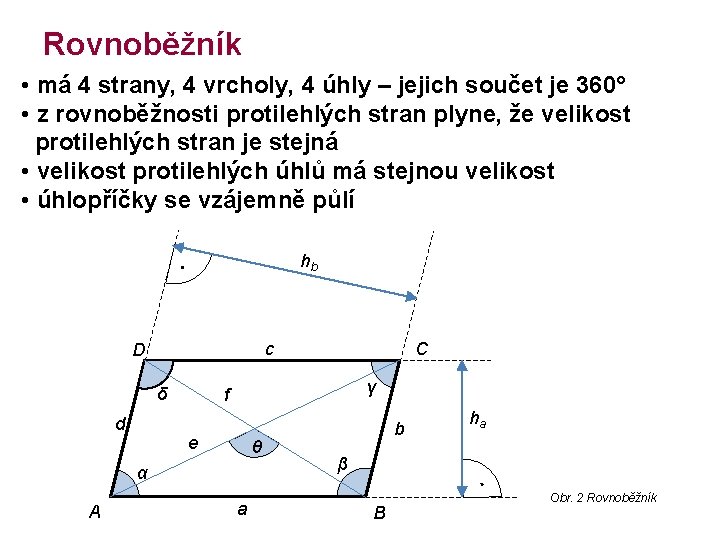
Rovnoběžník • má 4 strany, 4 vrcholy, 4 úhly – jejich součet je 360° • z rovnoběžnosti protilehlých stran plyne, že velikost protilehlých stran je stejná • velikost protilehlých úhlů má stejnou velikost • úhlopříčky se vzájemně půlí hb ∙ δ d γ f e θ b ha β ∙ α A C c D a B Obr. 2 Rovnoběžník

Čtverec • • pravidelný čtyřúhelník všechny vnitřní úhly jsou shodné protilehlé strany jsou rovnoběžné všechny strany jsou shodné, všechny vnitřní úhly jsou pravé • úhlopříčky čtverce jsou shodné a navzájem kolmé, půlí jeho úhly i sebe navzájem • čtverci lze jakožto pravidelnému mnohoúhelníku opsat i vepsat kružnici, je to zároveň tětivový čtyřúhelník i tečnový čtyřúhelník

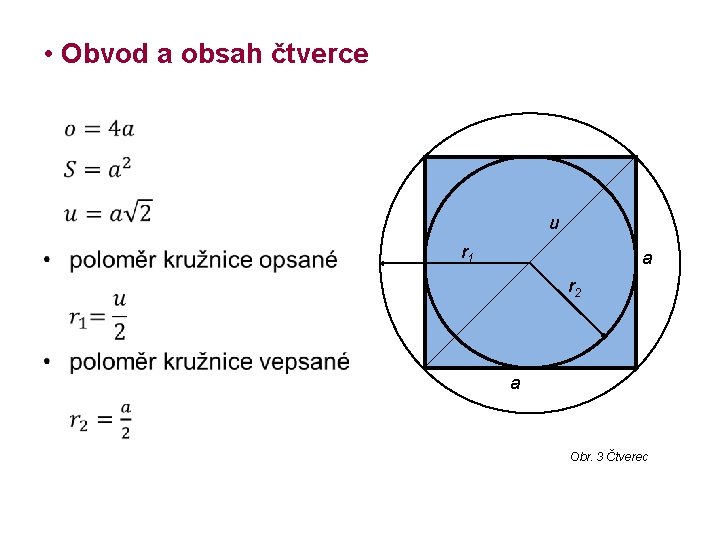
• Obvod a obsah čtverce • u r 1 a r 2 a Obr. 3 Čtverec

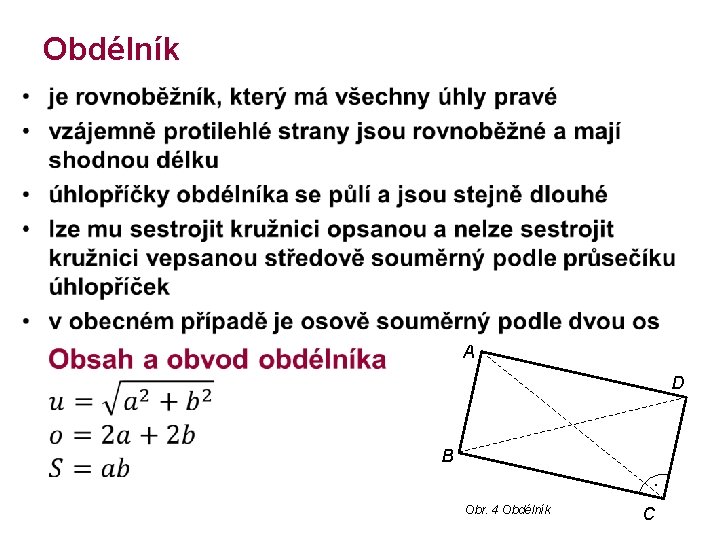
Obdélník • A D B ∙ Obr. 4 Obdélník C

Kosočtverec • • rovnostranný rovnoběžník má všechny strany stejně dlouhé jeho strany nesvírají pravý úhel má dvě úhlopříčky jeho úhlopříčky jsou na sebe kolmé má dvě osy souměrnosti lze vepsat kružnici C D ∙ A C ∙ D B B A Obr. 5 Kosočtverec 1

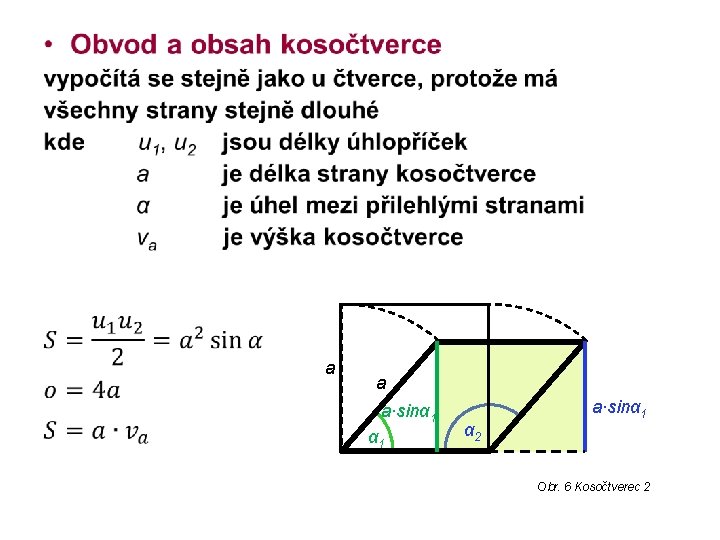
• a a a∙sinα 1 α 2 a∙sinα 1 Obr. 6 Kosočtverec 2

Lichoběžník • c D d A C v b ∙ a B Obr. 7 Lichoběžník

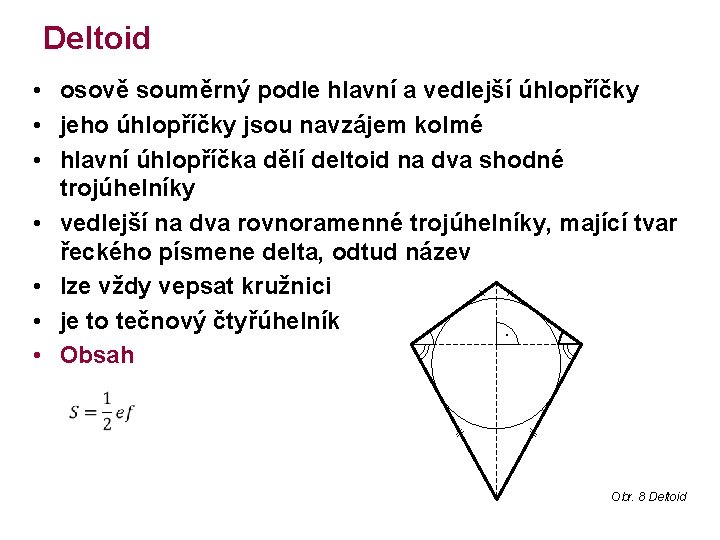
Deltoid • osově souměrný podle hlavní a vedlejší úhlopříčky • jeho úhlopříčky jsou navzájem kolmé • hlavní úhlopříčka dělí deltoid na dva shodné trojúhelníky • vedlejší na dva rovnoramenné trojúhelníky, mající tvar řeckého písmene delta, odtud název • lze vždy vepsat kružnici • je to tečnový čtyřúhelník ∙ • Obsah Obr. 8 Deltoid

Zdroje Obr. 1: Čtyřúhelníky. In: Wikipedia: the free encyclopedia [online]. San Francisco (CA): Wikimedia Foundation, 2001 -2011 [cit. 2013 -03 -20]. Dostupné z: http: //upload. wikimedia. org/wikipedia/commons/e/ef/Klasifikace_%C 4%8 Dty%C 5%99%C 3 %BAheln%C 3%ADk%C 5%AF. png Všechny neocitované grafické objekty jsou součástí MS Office. Autor: Mgr. Lubomíra Moravcová Název díla: Čtyřúhelníky Datum vzniku: březen 2013 Materiál je určen pro bezplatné používání pro potřeby výuky na všech typech škol a školských zařízení. Jakékoliv další využití podléhá autorskému zákonu. Tato prezentace je autorským dílem.