O Problema do Corte Unidimensional Indstrias de papel

O Problema do Corte Unidimensional Indústrias de papel, tecido, vidro, barras de aço , entre outras, fabricam seus produtos em peças de tamanho fixo (tamanho padrão). Estas peças são depois divididas em tamanhos menores a serem definidos de acordo com a necessidade do cliente. O problema do corte consiste em determinar como cortar o menor número de peças de tamanho padrão L, atendendo a uma demanda , bi, por itens de tamanho li, i=1, . . . , m. 2

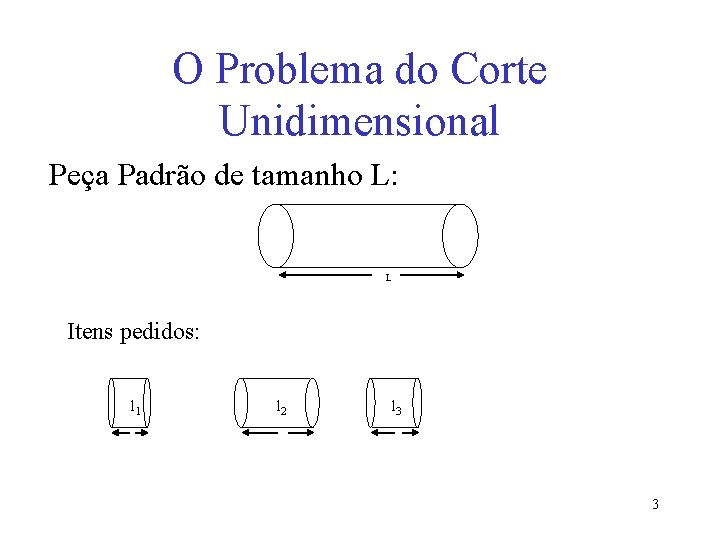
O Problema do Corte Unidimensional Peça Padrão de tamanho L: L Itens pedidos: l 1 l 2 l 3 3

O Problema do Corte Unidimensional Esquemas de corte: Esquema 1: 5 peças l 1 L l 1 l 1 l 1 4

O Problema do Corte Unidimensional Esquemas de corte: Esquema 1: 5 peças l 1 Esquema 2: 2 peças l 2 L l 1 l 1 l 1 L l 2 5

O Problema do Corte Unidimensional Esquemas de corte: Esquema 1: 5 peças l 1 Esquema 2: 2 peças l 2 Esquema 3: 1 peça l 2 2 peças l 3 L l 1 l 1 l 1 L l 2 l 3 6

O Problema do Corte Unidimensional Como Definir um Esquema de corte? Encontrar as soluções da seguinte equação: 7

O Problema da Mochila Inteiro

O Problema do Corte Unidimensional Vamos considerar um problema onde: L = 170 cm l 1= 30 cm, l 2=50 cm, l 3=55 cm e a demanda para os itens menores é: d 1= 80, d 2=120, d 3=110 Quantos esquemas de corte são possíveis? 9

O Problema do Corte Unidimensional Existem 27 esquemas de corte possíveis. Entre estes temos: 10

O Problema do Corte Unidimensional Existem 27 esquemas de corte possíveis. Entre estes temos: 11

O Problema do Corte Unidimensional Existem 27 esquemas de corte possíveis. Entre estes temos: 12

O Problema do Corte Unidimensional Existem 27 esquemas de corte possíveis. Entre estes temos: 13

O Problema do Corte Unidimensional Existem 27 esquemas de corte possíveis. Entre estes temos: 14

O Problema do Corte Unidimensional Existem 27 esquemas de corte possíveis. Entre estes temos: 15

Construindo um modelo para o Problema do Corte Unidimensional 16

Construindo um modelo para o Problema do Corte Unidimensional 17

Construindo um modelo para o Problema do Corte Unidimensional 18

Construindo um modelo para o Problema do Corte Unidimensional 19

Construindo um modelo para o Problema do Corte Unidimensional 20

Construindo um modelo para o Problema do Corte Unidimensional 21

Construindo um modelo para o Problema do Corte Unidimensional 22

Construindo um modelo para o Problema do Corte Unidimensional 23

Construindo um modelo para o Problema do Corte Unidimensional VARIÁVEIS DE DECISÃO Quantas vezes usar um determinado esquema de corte Faça j = 1, 2, 3, . . . n representar os diversos esquemas de corte Defina então: = número de vezes que o esquema de corte j será usado. 24

Construindo um modelo para o Problema do Corte Unidimensional Objetivo a Usar o menor número possível de esquemas de corte: Objetivo b Seja rj a perda associada ao esquema de corte j Minimizar a perda total: 25

Construindo um modelo para o Problema do Corte Unidimensional Restrições O número de itens obtidos de cada tipo deve ser maior ou igual a demanda. Seja aij o número de peças do tipo i obtidas usando o esquema de corte j. Para atender a demanda do item 1 temos que: De uma maneira geral, a restrição relativa ao item i é dada por: 26

Modelo de Otimização Para o Problema do Corte Unidimensional (Objetivo a) 27

Modelo de Otimização Para o Problema do Corte Unidimensional Podemos escrever as restrições do problema na forma matricial: Observe que cada coluna da matriz esta associada a um esquema de corte. Em geral n ==> Impossível de ser gerado ou mesmo armazenado: Geração de colunas - Problema da Mochila 28

Problema do Corte Unidimensional Exemplo 1 a • Considerando apenas 6 padrões de corte: 29

Problema do Corte Unidimensional Exemplo 1 a - Solução Considerando apenas 6 padrões de corte: LP OPTIMUM FOUND AT STEP 3 OBJECTIVE FUNCTION VALUE 1) 115. 0000 Usar: o esquema de corte 19 55 vezes At 19 = (2, 0, 2) o esquema de corte 24 60 vezes At 24 = (1, 2, 0) com sobra de 90 itens do tipo 1 30

Problema do Corte Unidimensional Exemplo 1 b • Considerando apenas 6 padrões de corte: 31

Problema do Corte Unidimensional Exemplo 1 b - Solução Considerando apenas 6 padrões de corte: LP OPTIMUM FOUND AT STEP 2 OBJECTIVE FUNCTION VALUE 1) 0. 0000000 E+00 Usar: o esquema de corte 19 55 vezes At 19 = (2, 0, 2) o esquema de corte 23 120 vezes At 23 = (4, 0, 1) teremos sobra de 510 itens do tipo 1 32

Esquemas de corte para o Problema do Corte Unidimensional - Exemplo 1 Existem 27 esquemas de corte 33

Problema do Corte Unidimensional Exemplo 1 a - Solução Considerando todos os esquemas de corte possíveis (27): Usar: o esquema de corte 3 30 vezes: At 3 = (0, 0, 3) o esquema de corte 13 20 vezes At 13= (0, 2, 1) o esquema de corte 25 40 vezes At 25= (2, 2, 0) Não há sobra de itens Custo total = 90 34

Problema do Corte Unidimensional Exemplo 1 b - Solução Considerando todos os esquemas de corte possíveis (27): Usar: o esquema de corte 19 55 vezes: At 19 = (2, 0, 2) o esquema de corte 23 120 vezes At 23= (4, 1, 0) Sobram 510 itens do tipo 1 Custo total = 0 35