O mtodo dos gradientes conjugados Francisco A M

O método dos gradientes conjugados Francisco A. M. Gomes MT 402 – Matrizes – junho de 2008

Funções quadráticas n Chamamos de quadrática uma função f(x): n que pode ser escrita na forma onde A n n, b n e c .

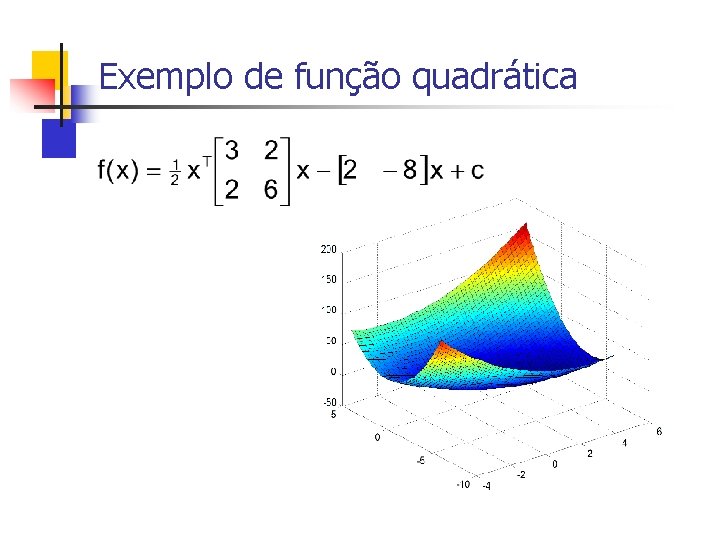
Exemplo de função quadrática

Curvas de nível da quadrática n Repare que as curvas de nível de f, neste exemplo, são elipses. n Em cada curva do gráfico, encontramos pontos com o mesmo valor de f.

Gradiente n n O gradiente de uma função f(x) é dado por Para um dado ponto x, o gradiente fornece a direção de maior crescimento de f(x).

Exemplo de gradiente n n n O gradiente é ortogonal à curva de nível. No exemplo, as setas apontam para o lado de fora das elipses, de modo que o ponto (2, -2) é o mínimo de f(x). Em (2, -2), temos f’(x) = 0.

Quadráticas e sistemas lineares n n De uma forma geral, escrevemos o gradiente de uma função quadrática f(x) na forma: Se a matriz A é simétrica, temos Podemos tentar minimizar uma função quadrática f(x) igualando o gradiente a zero. Isso equivale a resolver o sistema Ax = b.

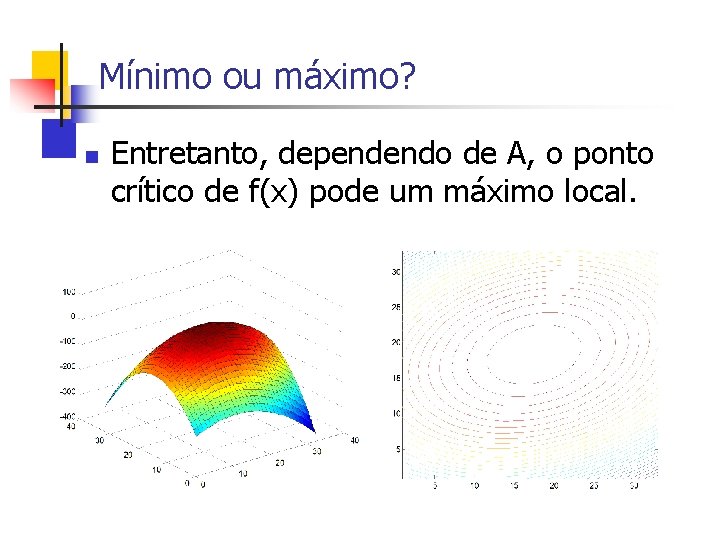
Mínimo ou máximo? n Entretanto, dependendo de A, o ponto crítico de f(x) pode um máximo local.

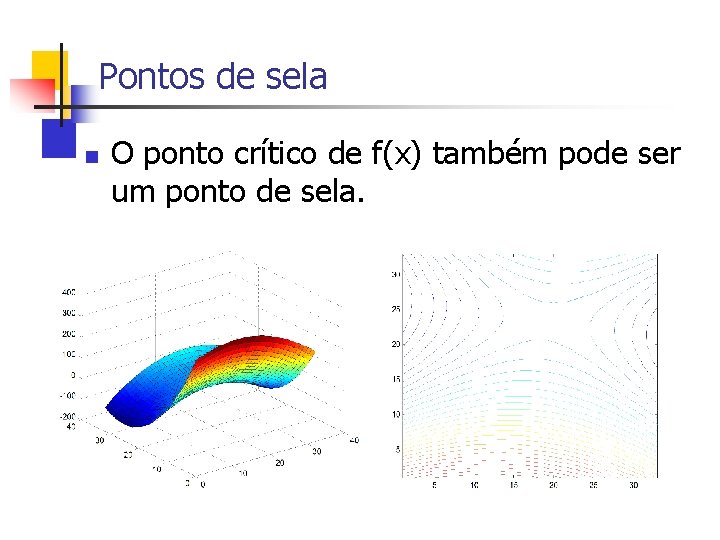
Pontos de sela n O ponto crítico de f(x) também pode ser um ponto de sela.

Matrizes definidas positivas n Se a matriz A, além de simétrica, é definida positiva, então a função quadrática f(x) é um parabolóide voltado para cima, e a solução de f’(x) = 0, ou de Ax = b, é o ponto de mínimo de f(x).

O método da máxima descida n Também chamado de método do gradiente. n n n Começa em um ponto x 0 arbitrário Gera uma seqüência de pontos x 1, x 2, . . . Caminha para o ponto de mínimo do parabolóide, x*, seguindo a direção do vetor –f´(x).

Definições importantes n n Erro em xi: ei = x* – xi. Resíduo em xi: ri = b – Axi. O resíduo pode ser visto como o erro transformado por A: ri = b – Axi = A(x* – xi) = Aei. O resíduo também pode ser visto como a direção de máxima descida de f(x) em xi: ri = –f’(xi).

Idéia do método n n Dado x 0, podemos encontrar um ponto x 1 que diminua o resíduo (ou f(x)), dando um passo na direção de –f ’(x 0). Em outras palavras, podemos encontrar x 1 definido como x 1 = x 0 + r 0. n O parâmetro é denominado comprimento do passo.

Definindo o tamanho do passo n Para encontrar o melhor valor de , minimizamos f(x) ao longo da direção definida por r 0, ou seja, fazemos uma busca linear: n minimiza f(x 0 + r 0) é determinado igualando a zero a derivada de f(x 0 + r 0) com relação a :

Algoritmo n Este procedimento é repetido por várias iterações, até que xi esteja suficientemente próximo de x*.

Taxa de convergência n n n Infelizmente, o método do gradiente não possui, em geral, boa taxa de convergência. Na verdade, podemos provar apenas que onde é o número de condição de A. Assim, se A tem um número de condição alto, pouco podemos esperar deste método.

Hiperelipsóides alongados n n n Quando (A) é alto, as curvas de nível de f(x) são hiperelipsóides muito alongados. Para exemplificar isso, vamos resolver o sistema Ax = b com Neste caso, (A) = 1. 0201 e+005.

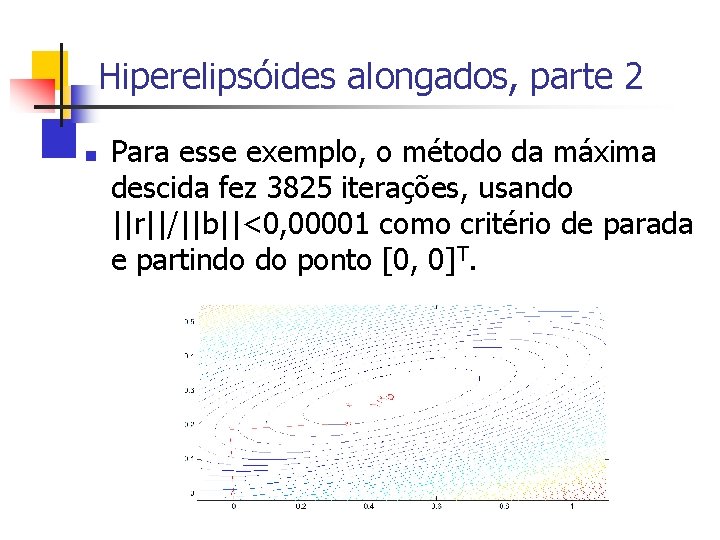
Hiperelipsóides alongados, parte 2 n Para esse exemplo, o método da máxima descida fez 3825 iterações, usando ||r||/||b||<0, 00001 como critério de parada e partindo do ponto [0, 0]T.

O método dos gradientes conjugados n n É um método que usa a mesma fórmula recursiva do método do gradiente, ou seja, xk+1 = xk + kdk, Mas que não usa como vetor direção o resíduo no ponto xk: dk rk = b – Axk.

Idéia geral do método n 1. 2. Vamos tentar encontrar, a cada iteração k, um vetor dk que seja linearmente independente dos anteriores d 0, . . . , dk-1; faça com que xk+1 minimize f(x) no espaço gerado pelos vetores d já definidos. (Naturalmente, esse espaço é o subespaço de Krylov K(A, d 0, k))

Idéia geral do método, parte 2 n Assim, xk+1 deve resolver o problema n onde Dk é a matriz cujas colunas são os vetores d 0, . . . , dk. Desta forma, ao final de n iterações, teremos minimizado f(x) em n, obtendo, assim, a solução do sistema linear Ax = b.

Encontrando w n Para obter uma expressão computável para xk+1, substituímos o termo xk+1 = xk + Dk w na fórmula de f(xk+1):

Encontrando w, parte 2 n n Derivando f(xk+1) com relação a w, obtemos um ponto de mínimo dado por Deste modo,

Vetores ortogonais n n Constatamos que rk+1 é ortogonal aos vetores di (colunas de Dk), pois Assim, dj. Trk+1 = 0, para j = 1, . . . , k.

Vetores ortogonais, parte 2 n n Se, nas iterações anteriores, os valores de xj, j = 1, . . . , k, também foram obtidos de modo a minimizar f(xj-1 + Dj-1 wj-1), concluímos, por indução, que dj. Tri = 0 para j < i. Substituindo este termo na expressão de xk+1, temos onde = dk. Trk e ek corresponde à késima coluna da identidade.

Usando vetores A-conjugados n n Para simplificar a expressão de xk+1 e facilitar os cálculos, podemos tentar fazer com que a matriz Dk. TADk seja diagonal. Para tanto, basta exigirmos que os vetores dj sejam A-conjugados, ou seja, que di. TAdj = 0 para i j.

Como obter vetores A-conjugados n 1. 2. Lembrando que a iteração do método é definida por podemos obter um conjunto de direções A -conjugadas: Escolhendo d 0 = r 0 (como no método da máxima descida) Definindo rk como uma combinação linear de d 0, . . . , dk, de modo que (1)

Como obter vetores A-conjugados (2) n Desta última equação, obtemos n Como as direções dj são A-conjugadas, n Mas n n , de modo que Uma vez que, de (1), temos ri. Trj = 0, i j, Concluímos que kj = 0, j = 1, . . . , k – 2.

Como obter vetores A-conjugados (3) n Apenas k, k-1 0. Chamemos de k este valor n Claramente n Como n Obtemos n E como, de (1), temos n Chegamos a n Assim, a expressão de dk torna-se

Algoritmo n 1. 2. 3. 4. Dados de entrada: A matriz A (simétrica, definida positiva). O vetor b. Uma aproximação inicial x 0 da solução do sistema. Os parâmetros (tolerância do resíduo) e kmax (número máximo permitido de iterações).

Algoritmo, parte 2 n 1 r 0 b – Ax 0 n 2 k 0; -1 0; d-1 0 n 3 Enquanto ||rk||2/||b||2 > e k kmax, n 3. 1 dk rk + k dk-1 n 3. 2 k rk. Trk/dk. TAdk n 3. 3 xk+1 xk + kdk n 3. 4 rk+1 rk – k. Adk n 3. 5 n 3. 6 k k+1

Convergência do método n n n Teoricamente, o método converge para a solução do sistema linear em n iterações. Entretanto, nem sempre isso acontece em virtude dos erros de arredondamento e cancelamento que fazem com que n o vetor resíduo perca precisão; n os vetores direção deixem de ser Aconjugados, ou seja, Isso ocorre quando A é mal condicionada.

Exemplo com A bem condicionada n n n n » A = sprand(100, 0. 05, 0. 5) +0. 1*speye(100); » A = A'*A; » condest(A) ans = 11. 085 » b = rand(100, 1); » x = pcg(A, b); pcg converged at iteration 15 to a solution with relative residual 9. 8 e-007

Exemplo com A mal condicionada n n n n n » A = sprand(100, 0. 05, 0. 0001) +0. 1*speye(100); » A = A'*A; » condest(A) ans = 3. 7142 e+008 » x = pcg(A, b); pcg stopped at iteration 20 without converging to the desired tolerance 1 e-006. . . » x = pcg(A, b, 1 e-5, 1000); pcg converged at iteration 232 to a solution with relative residual 2. 6 e-006

Taxa de convergência n n Assim, a distância entre f(xi) e f(x*) está limitada por um termo que é próximo de 1 se k(A) é grande. Felizmente, o método costuma convergir mais rápido do que podemos prever, principalmente quando precondicionado.