NUMEROS COMPLEJOS 1 NMEROS COMPLEJOS El inicio del

NUMEROS COMPLEJOS -1

NÚMEROS COMPLEJOS El inicio del estudio de los números complejos o imaginarios surge con la necesidad de resolver algunas situaciones que no podían realizarse con los conjuntos de números que se habían descubierto en ese entonces. Las preguntas más comunes era ¿Cuál es el resultado de? Ediciones Zorrilla SRL Mejorando la educación

NÚMEROS COMPLEJOS Según la historia dos matemáticos concibieron la idea de un número no real y aptaron por llamarle Número imaginario, términos que muchos matemáticos de ese tiempo no aceptaron. Ediciones Zorrilla SRL Mejorando la educación

NÚMEROS COMPLEJOS Los números complejos son la herramienta de trabajo del álgebra, análisis, así como de ramas de las matemáticas puras y aplicadas como variable compleja, ecuaciones diferenciales, aerodinámica y electromagnetismo entre otras de gran importancia. Ediciones Zorrilla SRL Mejorando la educación

UTILIDAD DE NÚMEROS COMPLEJOS En Circuitos Eléctricos La base matemática de los Circuitos Eléctricos son los números complejos. Por ejemplo, amplificadores, filtros, motores, generadores de energía eléctrica, líneas de transmisión de energía eléctrica. Circuitos de medición y control, y todo eso se aplica en varias partes: en medicina se utiliza para la espectrometría, en transmisión y recepción de señales electromagnéticas (radio, TV, celular, teléfono, etc). Facilitar el estudio de cargas Sobre vigas(para los arquitectos e ingenieros civiles), estudio de ondas(para los físicos), http: //unatazadecafedesesperada. blogspot. com/2012/06/numeros-complejos-e-imaginarios-en-la. htm Ediciones Zorrilla SRL Mejorando la educación

Ediciones Zorrilla SRL Mejorando la educación

NÙMEROS COMPLEJOS Llamamos números complejos a los números de la forma a + bi, donde a y b son números reales e i es la unidad imaginaria. -9+6 i Ediciones Zorrilla SRL Mejorando la educación

PARTES DE UN NÚMERO COMPLEJO Números Complejos Parte real 6 -3 i 0+5 i -4+0 i Ediciones Zorrilla SRL Mejorando la educación Parte imaginaria Clasificación

El complejo opuesto Z (complejo) 3+2 i -3 -7 i 8 -4 i Ediciones Zorrilla SRL Mejorando la educación -z (opuesto)

Binómica de complejos Par ordenado Ediciones Zorrilla SRL Mejorando la educación Binómica

PAR ORDENADO DE UN NÚMERO COMPLEJO z= (a, b) par ordenado Z (complejo) 3+i 4 -7 i 6 i -4 -5 -6 i Ediciones Zorrilla SRL Mejorando la educación Z (Par ordenado)

CONJUGADO DE UN NÚMERO COMPLEJO Z (complejo) Z (Conjugado) 3+2 i 4 -7 i -8+4 i -4 -3 i -6 i Proverbio 22: 28 No traspases los linderos antiguos que pusieron tus padres. Ediciones Zorrilla SRL Mejorando la educación

CONJUGADO DE UN NÚMERO COMPLEJO Z (complejo) Z (Conjugado) 3+2 i 4 -7 i -6 i Proverbio 22: 28 No traspases los linderos antiguos que pusieron tus padres. Ediciones Zorrilla SRL Mejorando la educación

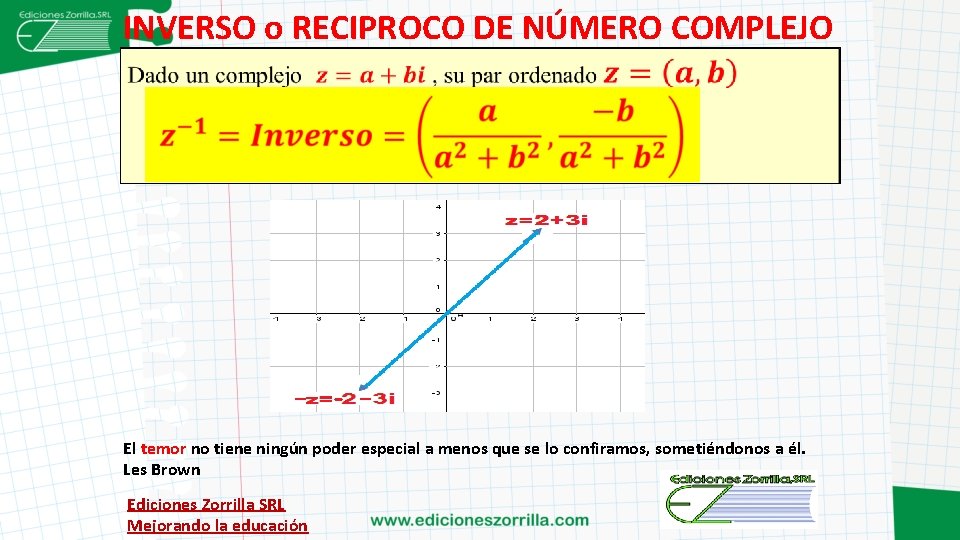
INVERSO o RECIPROCO DE NÚMERO COMPLEJO El temor no tiene ningún poder especial a menos que se lo confiramos, sometiéndonos a él. Les Brown Ediciones Zorrilla SRL Mejorando la educación

INVERSO o RECIPROCO DE NÚMERO COMPLEJO Z (complejo) La perseverancia es el eje de todas las virtudes. (Carlyle). Ediciones Zorrilla SRL Mejorando la educación