Numerisches Programmieren bung 3 Adrian Schultz Thema Interpolation

Numerisches Programmieren – Übung 3 Adrian Schultz Thema: Interpolation

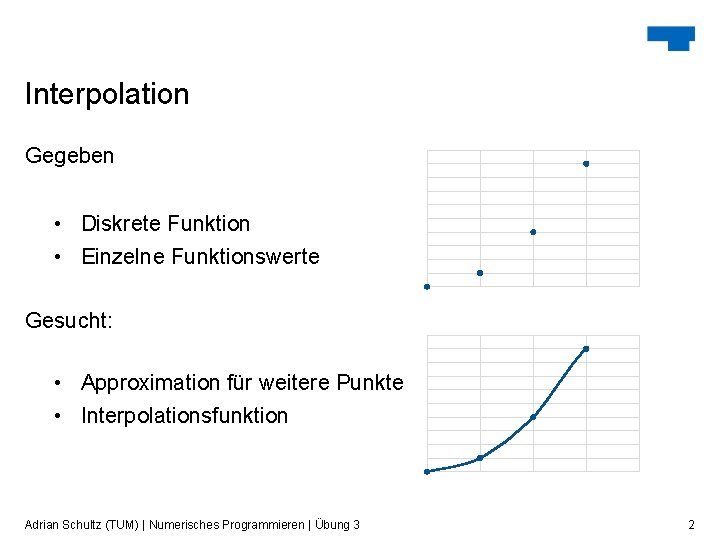
Interpolation Gegeben • Diskrete Funktion • Einzelne Funktionswerte Gesucht: • Approximation für weitere Punkte • Interpolationsfunktion Adrian Schultz (TUM) | Numerisches Programmieren | Übung 3 2

Gängige Basisfunktionen Adrian Schultz (TUM) | Numerisches Programmieren | Übung 3 3

Interpolationsfunktion Adrian Schultz (TUM) | Numerisches Programmieren | Übung 3 4

Interpolationsfunktion Adrian Schultz (TUM) | Numerisches Programmieren | Übung 3 5

Newton Verfahren Adrian Schultz (TUM) | Numerisches Programmieren | Übung 3 6

Newton Verfahren Adrian Schultz (TUM) | Numerisches Programmieren | Übung 3 7

Newton Verfahren Adrian Schultz (TUM) | Numerisches Programmieren | Übung 3 8

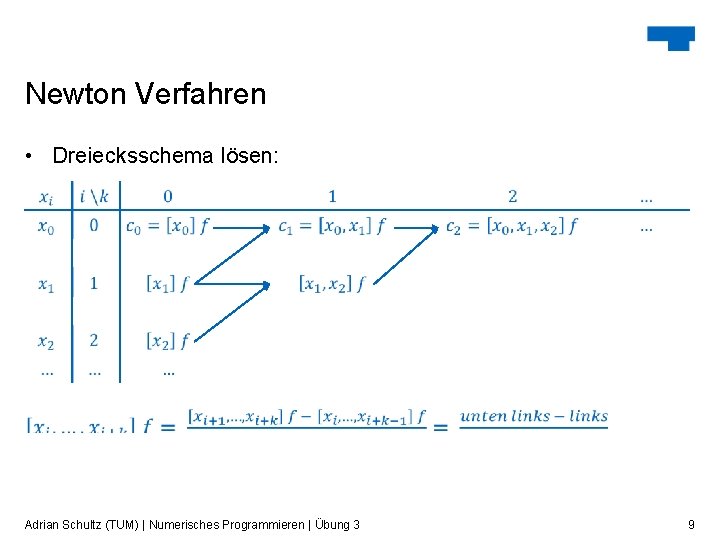
Newton Verfahren • Dreiecksschema lösen: Adrian Schultz (TUM) | Numerisches Programmieren | Übung 3 9

Newton Verfahren Adrian Schultz (TUM) | Numerisches Programmieren | Übung 3 10

Interpolation nach Aitken-Neville Adrian Schultz (TUM) | Numerisches Programmieren | Übung 3 11

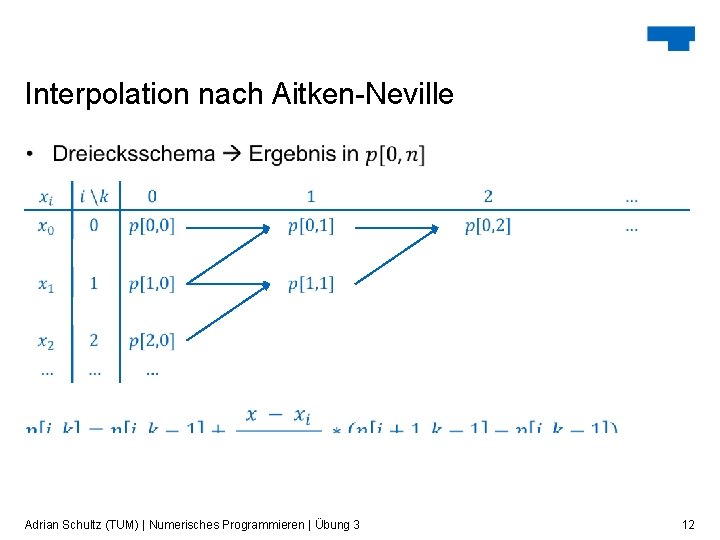
Interpolation nach Aitken-Neville Adrian Schultz (TUM) | Numerisches Programmieren | Übung 3 12

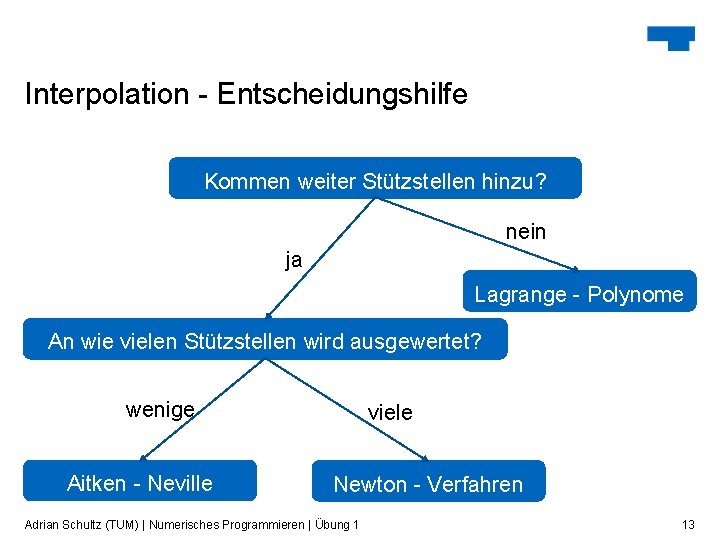
Interpolation - Entscheidungshilfe Kommen weiter Stützstellen hinzu? nein ja Lagrange - Polynome An wie vielen Stützstellen wird ausgewertet? wenige Aitken - Neville viele Newton - Verfahren Adrian Schultz (TUM) | Numerisches Programmieren | Übung 1 13

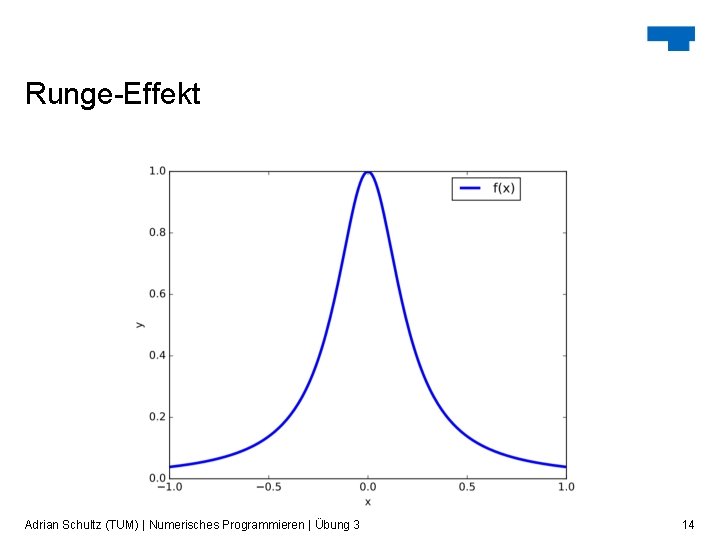
Runge-Effekt Adrian Schultz (TUM) | Numerisches Programmieren | Übung 3 14

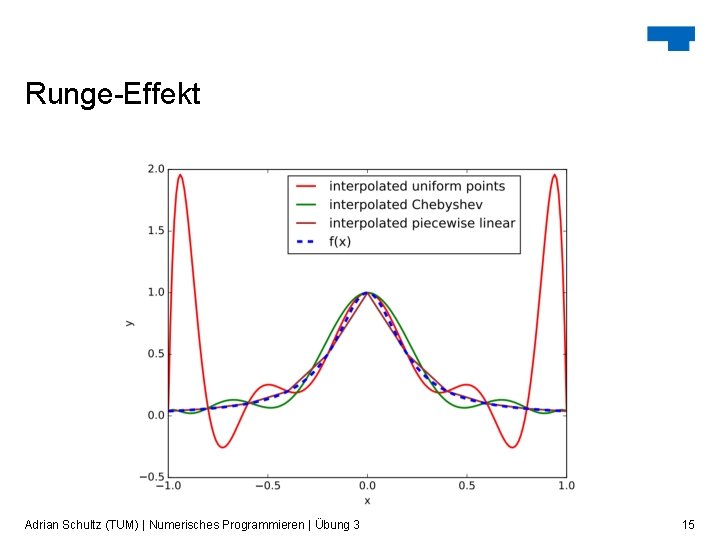
Runge-Effekt Adrian Schultz (TUM) | Numerisches Programmieren | Übung 3 15

Runge-Effekt Probleme einer Polynominterpolation mit vielen Stützstellen: oft sehr große Ausschläge am Rand • ab bestimmten Punkt nicht genauer • Lösungsmöglichkeiten: • Variation der Basisfunktionen • Stückweise Interpolation Adrian Schultz (TUM) | Numerisches Programmieren | Übung 3 16

Geschafft! Bei Fragen: • e-Mail an adrian. schultz@tum. de • oder jetzt noch kurz vorkommen Bis nächste Woche! Adrian Schultz (TUM) | Numerisches Programmieren | Übung 3 17