Numerical Weather Forecast Model governing equations Momentum equations

Numerical Weather Forecast Model (governing equations) Momentum equations Mass continuity equation Moisture equation Ideal gas law Thermodynamic equation

Numerical Weather Forecast Model (governing equations) Vertical momentum equation Non-hydrostatic Hydrostatic assumption (large scale phenomena):

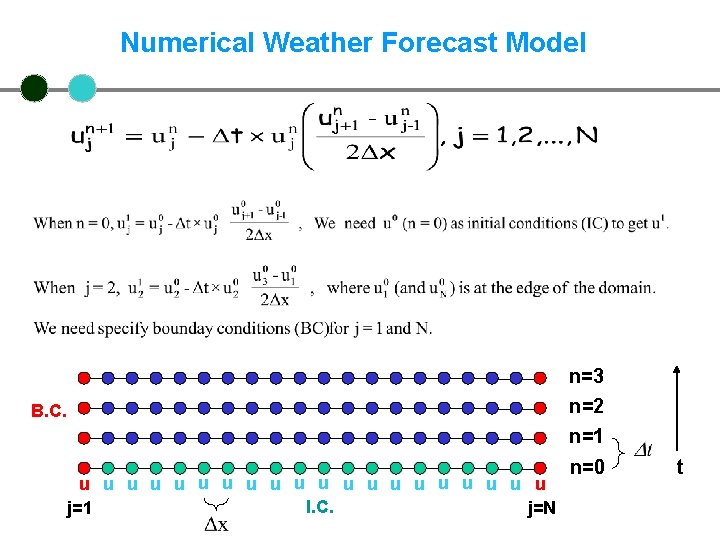
Numerical Weather Forecast Model Discretized in space (mesh) J-2 J-1 j Model grid points (boxes) J+1 x Discretized in time n-2 n-1 n n+1 t

Numerical Weather Forecast Model Let’s simplify the equation to for now How do we discretize it? J-2 J-1 j J+1

Numerical Weather Forecast Model n=3 n=2 n=1 B. C. u u u u u I. C. j=1 j=N n=0 t

Descretization Resolutions: 1 n o ti T e u r lu o s y=x 2

Numerical Weather Forecast Model Global model vs. regional model Regional model

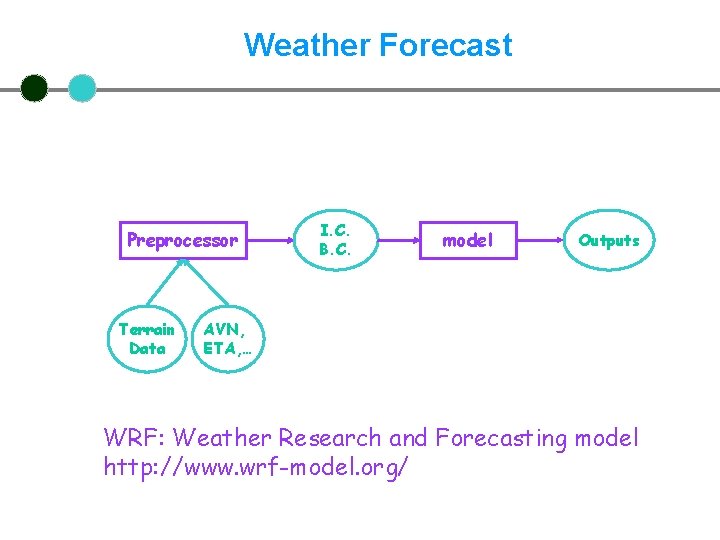
Weather Forecast Preprocessor Terrain Data I. C. B. C. model Outputs AVN, ETA, … WRF: Weather Research and Forecasting model http: //www. wrf-model. org/

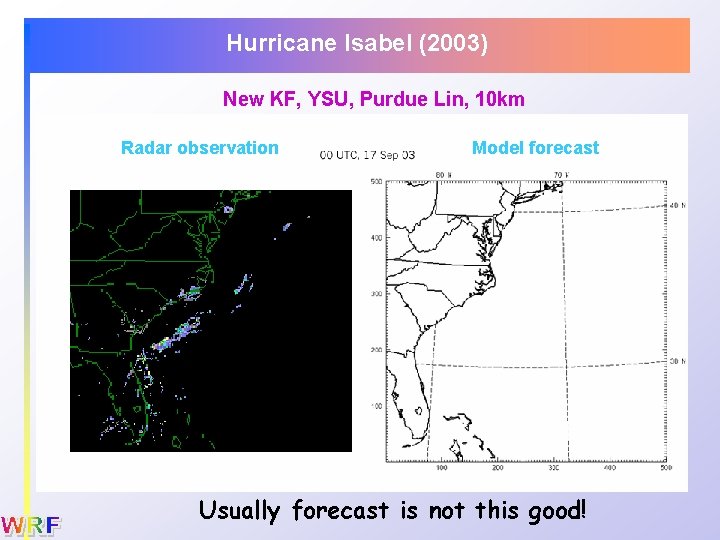
Hurricane Isabel (2003) New KF, YSU, Purdue Lin, 10 km Radar observation Model forecast Usually forecast is not this good!

MM 5 Model Configuration . Global Data: NCEP GDAS Domain 1 - 81 km 2 - 27 km 3 - 9 km Physic schemes: • • Betts-Miller convective scheme Blackadar PBL Mixed phase microphysics Simple radiation 48 -h simulation from 00 Z 17 July 1997

Hurricane Danny Initial Conditions (SLP, 950 mb wind vectors) (950 mb moisture) OBS 1011. 5 mb Analysis . 1013. 5 mb Reanalysis from global model

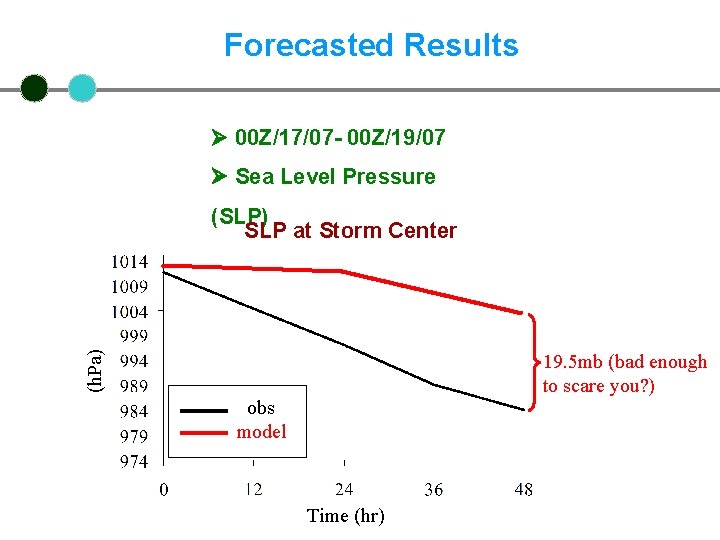
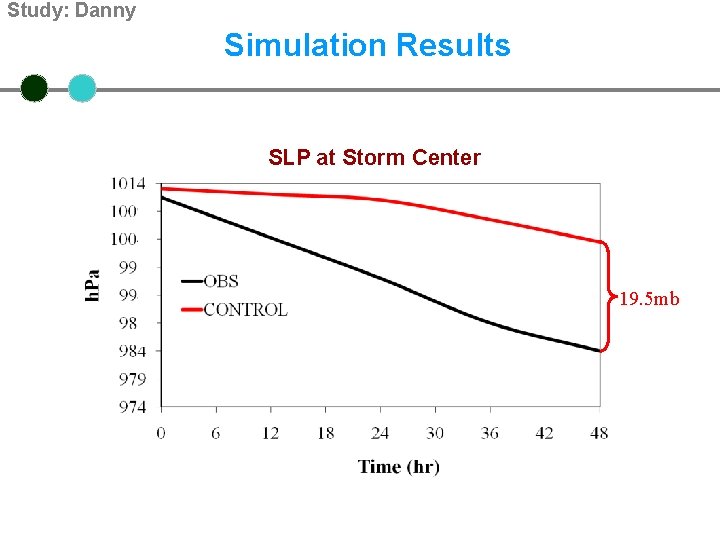
Forecasted Results 00 Z/17/07 - 00 Z/19/07 Sea Level Pressure (h. Pa) (SLP) SLP at Storm Center 19. 5 mb (bad enough to scare you? ) obs model Time (hr)

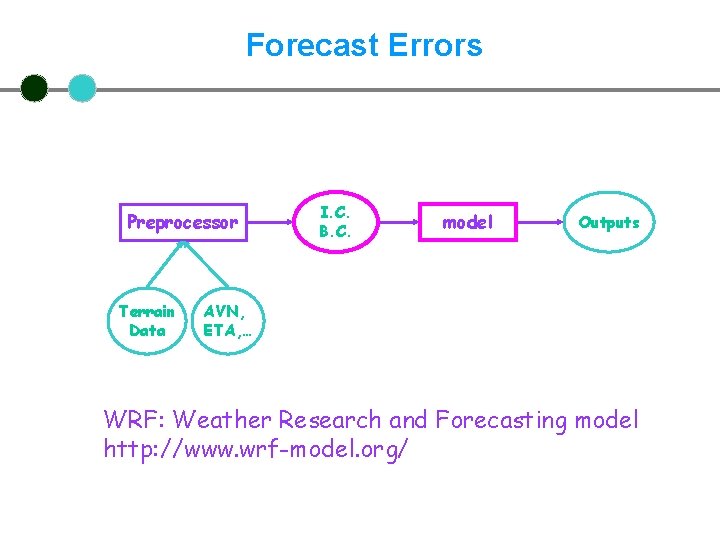
Forecast Errors Preprocessor Terrain Data I. C. B. C. model Outputs AVN, ETA, … WRF: Weather Research and Forecasting model http: //www. wrf-model. org/

Forecast Errors 1. Model Errors: Dynamics (numerical schemes) Physics parameterization Resolution 2. Initial and boundary conditions (I. C/B. C. ) error

Discretization (resolution) Resolutions: 1 0. 01 (more accurate) Usually Dt is proportional to Dx. => the higher the resolution, the more the computational time! n o ti T e u r u l so Dx==0. 1 0. 01 Dx Dx =1

Problems of I. C. • Reanalysis data – coarse resolution Errors in I. C. Lack of mesoscale features in I. C. Model spin-up problem

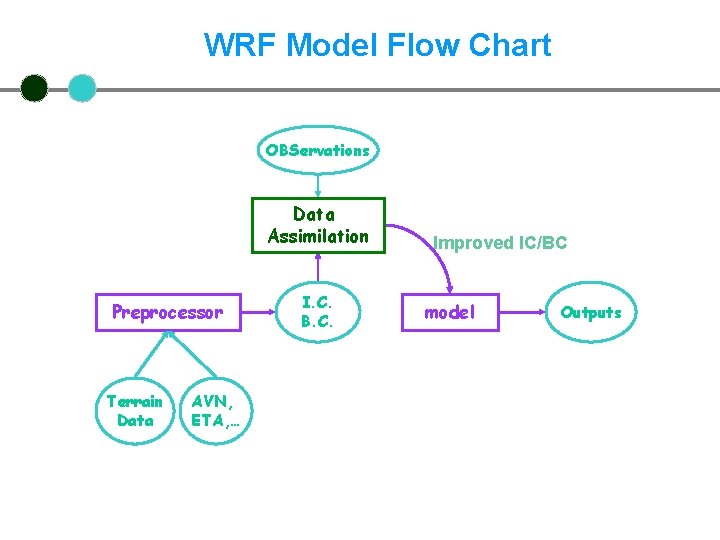
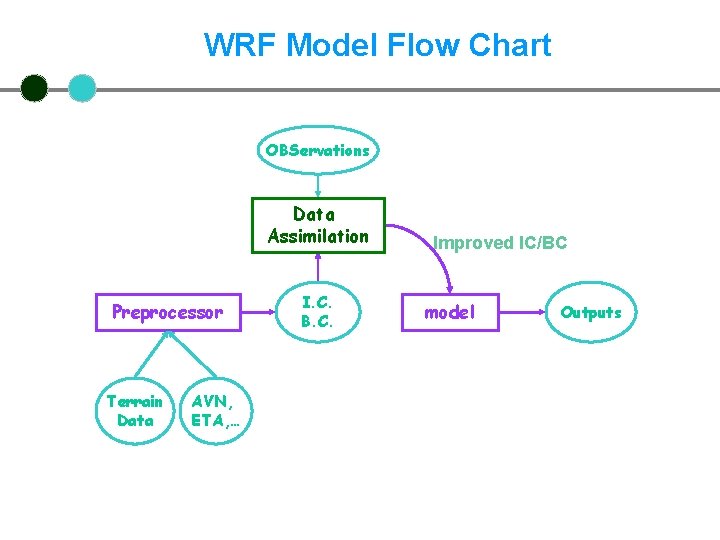
WRF Model Flow Chart OBServations Data Assimilation Preprocessor Terrain Data AVN, ETA, … I. C. B. C. Improved IC/BC model Outputs

Conventional Observations 12 z 65 upper air soundings, 866 surface stations

Problems • Reanalysis data – coarse resolution Error in I. C Lack of mesoscale features in I. C. Model spin-up problem • Coarse resolution of World Meteorological Organization Upper-air radiosondes Twice a day Several hundred km resolution • Conventional data sparse areas Ocean Antarctic

Need Unconventional Observations Remote Sensing Data Quik. SCAT

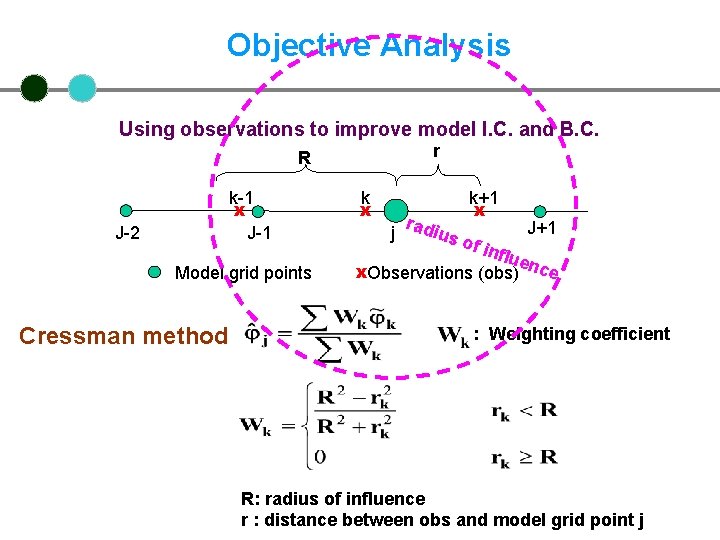
Objective Analysis Using observations to improve model I. C. and B. C. r R k-1 x J-1 J-2 Model grid points Cressman method k x k+1 x r J+1 j adius o f inf luen x. Observations (obs) ce : Weighting coefficient R: radius of influence r : distance between obs and model grid point j

Estimation and Data Assimilation = Suppose Tm = 18 C (model temperature) To = 21 C (observed temperature) = Suppose m = 2 C (model error) o = 1 C (observational error) = T is sought as: T = a Tm + b To = Such that the expected error: E{ ( T-Tt )2 } is minimal Cost function

Introduction Optimal Estimation T = a Tm + b To = Optimal solution o 2 a= o 2 + m 2 T = Tm + b= m 2 o 2 + m 2 Optimal nudging coefficient T = 20. 4 o C m 2 o 2 + m 2 ( To – Tm ) Tm = 18 C (model) To = 21 C (obs) m = 2 C (model) o = 1 C (obs)

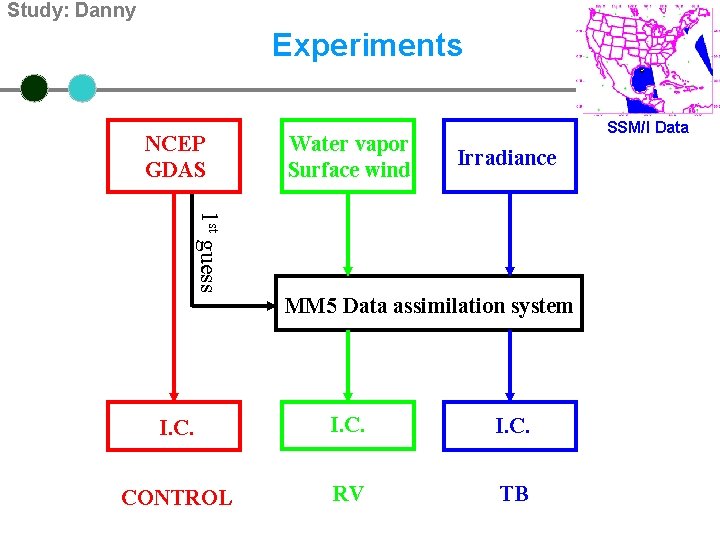
Study: Danny, 1997 o To comcompare two different approaches for assimilating SSM/I data Retrieved products: Total precipitable water (TPW) Sea surface wind (SSW) Raw measurements: Brightness temperature (Tb)

Study: Danny MM 5 Model Configuration . Global Data: NCEP GDAS Domain 1 - 81 km 2 - 27 km 3 - 9 km Physic: • • Betts-Miller convective scheme Blackadar PBL Mixed phase microphysics Simple radiation 48 -h simulation from 00 Z 17 July 1997

WRF Model Flow Chart OBServations Data Assimilation Preprocessor Terrain Data AVN, ETA, … I. C. B. C. Improved IC/BC model Outputs

Study: Danny Experiments NCEP GDAS Water vapor Surface wind SSM/I Data Irradiance 1 st guess MM 5 Data assimilation system I. C. CONTROL RV TB

Study: Danny Simulation Results SLP at Storm Center 19. 5 mb

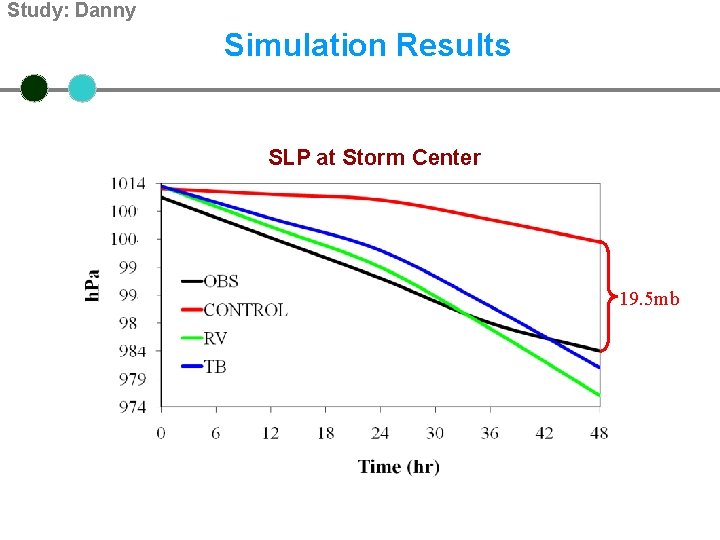
Study: Danny Simulation Results SLP at Storm Center 19. 5 mb

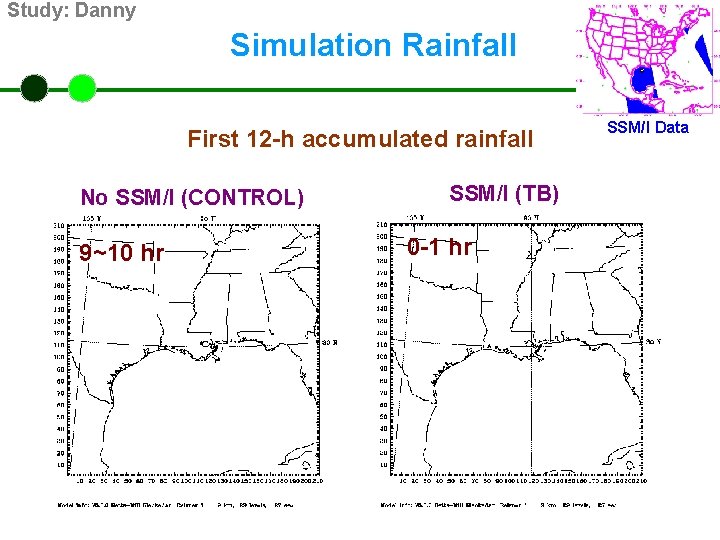
Study: Danny Simulation Rainfall First 12 -h accumulated rainfall No SSM/I (CONTROL) 9~10 hr SSM/I (TB) 0 -1 hr SSM/I Data