Numerical Techniques of Natural Circulation History and Background

Numerical Techniques of Natural Circulation: History and Background Juan Carlos Ferreri Autoridad Regulatoria Nuclear, Buenos Aires, Argentina Course on Natural Circulation Phenomena and Modelling in Water-cooled Nuclear Reactors ICTP, Trieste, Italy, 25 to 29 June, 2007

ICTP, 2007 CONTENTS ü Purpose of this presentation and introductory remarks ü On numerical methods ü A brief review of present status of CFD in relation to natural circulation, best practices and other issues ü Conclusions 2

ICTP, 2007 This presentation is aimed at considering several aspects of Numerical Techniques giving the background to the computation of Fluid Dynamics as applied to the Computational Fluid Dynamics (CFD) of Natural Circulation (NC). It will be shown that: a. There is plenty of consolidated literature and concepts on numerical methods since 50 years ago. b. CFD is not a new activity in relation to NC and thermal hydraulics of Nuclear Safety c. Many outstanding people contributed to this subject in the last five decades PURPOSE OF THIS PRESENTATION 3

ICTP, 2007 d. The present boom of CFD activity in NC and on separate effects in nuclear installations is a consequence of the needs of a re-emerging activity e. Nuclear Safety benefits from well developed techniques in other areas of computational mechanics f. Although some spectacular CFD results may be found at TH fora and in open (www) sources, not so many are already published in regular journals. g. Most publications deal with the needs and challenges posed by the physics and with clarifying the degree of detail required by nuclear safety PURPOSE OF THIS PRESENTATION 4

ICTP, 2007 Two possible definitions in this context: • A numerical technique is an incremental (or discrete) way of representing a differential equation (that is part of a physical model in NC) • Computational Fluid Dynamics is a discipline that allows solving conservation equations using adequate discrete representations at a desired level of resolution, implying more than a numerical technique INTRODUCTORY REMARKS 5

ICTP, 2007 On pioneers… Obviously, numerical techniques applications are not a new activity in relation to thermal hydraulics of all the flow stages of transients in nuclear installations (NC among others). In my view, it was the work at Los Alamos Scientific Laboratory which (now more than 30 years ago), in those days of “open” exchange of scientific information, opened the way to “widespread” numerical modeling in fluid dynamics. See, e. g. : Los Alamos Science, vol. 2, no. 2, summer/fall 1981 summarizing work done up to that year at LANL INTRODUCTORY REMARKS 6

ICTP, 2007 People, people… Many outstanding people contributed to this activity in the last 50 years. . . However, again in my view, LANL pioneered in this subject and its most relevant people were: Francis H. Harlow, J. Fromm, C. W. Hirt, D. L. Liles, J. Mahaffy, A. A. Amsdem, J. R. Travis, J. P. Shanon, J. Pryor and B. J. Daly, among others. Perhaps you have heard about codes like PIC, SOLASURF, SOLA-DF, SOLA-VOF, SALE-3 D, SOLALOOP, KFIX, etc. (see J. Comp. Physics) P. Roache gave also an important and comprehensive review and recommendations on numerical techniques and CFD by 1972. People at LLNL also contributed significantly INTRODUCTORY REMARKS 7

ICTP, 2007 People, people… Other people pioneered in Europe, like B. Spalding, M. Wolfshtein, S. Patankar at Imperial College, R. Peiret at ONERA and many others. I will just mention some people that contributed to the development from the numerical analysis side. . . …because the list is too long, but the names of R. Courant, K. O. Friedrichs, D. Hilbert, J. von Neumann, P. D. Lax, R. D. Richtmyer, G. I. Marchuk (in Russia) and W. F. Ames should, at least, be mentioned. INTRODUCTORY REMARKS 8

ICTP, 2007 People, people… The Drift-Flux theory of two-phase flow, as developed by Zuber and Findlay and by M. Ishii in his book, was the physical two-phase fluid model that allowed generating results of Nuclear Safety significance through its implementation in the TRAC code and other hydrodynamics codes at LASL. Many other people contributed significantly in this field, like J. M. Delhaye, R. Lahey, M. Giot, F. H Moody, G. B. Wallis, R. E. Henry, J. A. Bouré, D. C. Groeneveld, G. Yadigaroglu and simply too many others to be cited here… INTRODUCTORY REMARKS 9

ICTP, 2007 An appropriate conceptual excerpt… • “In as much as we can simulate reality, we can use the computer to make predictions about what will occur in a certain set of circumstances. • Finite-difference techniques can create an artificial laboratory for examining situations which would be impossible to observe otherwise, but we must always remain critical of our results. • Finite-differencing can be an extremely powerful tool, but only when it is firmly set in a basis of physical meaning. In order for a finite-difference code to be successful, we must start from the beginning, dealing with simple cases and examining our logic each step of the way. ” Reference: E. Scannapieco and Francis H. Harlow, Introduction to Finite-Difference Methods for Numerical Fluid Dynamics, LA 12984, issued 1995 INTRODUCTORY REMARKS 10

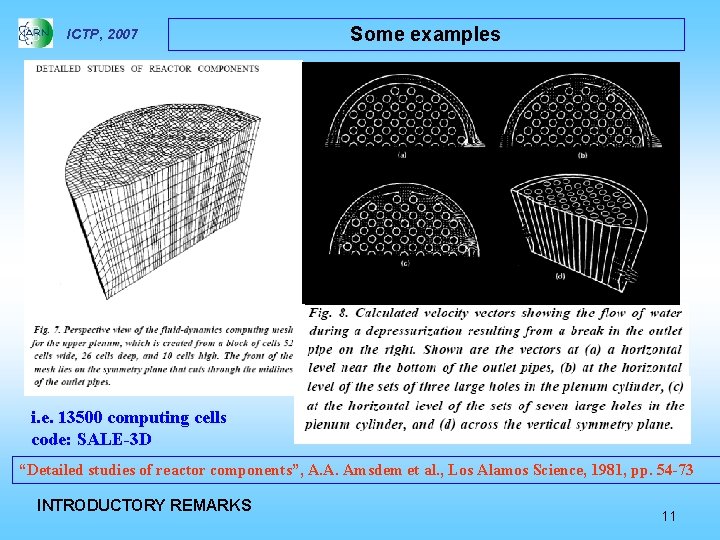
ICTP, 2007 Some examples i. e. 13500 computing cells code: SALE-3 D “Detailed studies of reactor components”, A. A. Amsdem et al. , Los Alamos Science, 1981, pp. 54 -73 INTRODUCTORY REMARKS 11

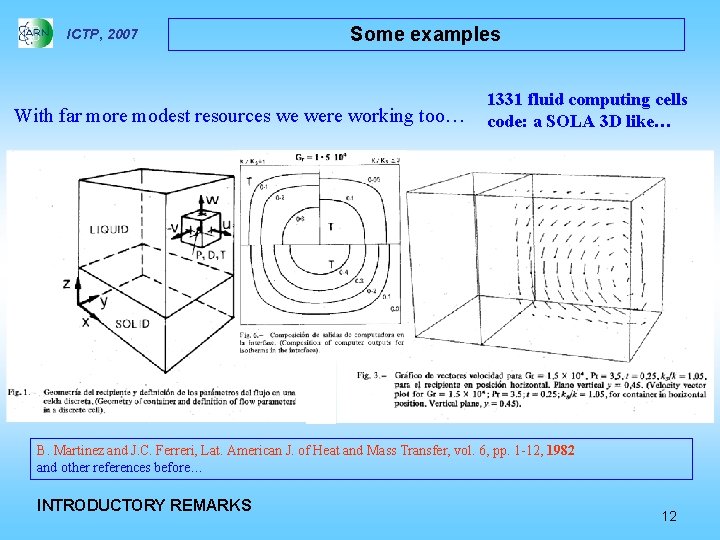
ICTP, 2007 Some examples With far more modest resources we were working too… 1331 fluid computing cells code: a SOLA 3 D like… B. Martinez and J. C. Ferreri, Lat. American J. of Heat and Mass Transfer, vol. 6, pp. 1 -12, 1982 and other references before… INTRODUCTORY REMARKS 12

A proposal for what follows… ICTP, 2007 Understanding the need of making efforts in the appropriate modelling of 1 D flows fluid dynamics (this seems a somewhat old-fashioned proposal at this time, when multidimensional CFD modelling governs the trends in the analysis of NC and separate effects in Nuclear Safety related issues) However, let´s make. . . INTRODUCTORY REMARKS 13

ICTP, 2007 A small digression on scaling laws… For single-phase flows in vertical pipes (or two-phase flows with equal velocities and temperature), the effects of each term in the conservation equations are preserved in model and prototype without any distortion, if one imposes the requirements of: a) Same fluid at equal pressure, properties and enthalpy: b) Isochronous phenomena: They lead to the Power to Volume scaling relations, i. e. : Where m is chosen on the basis of available resources, usually power for the model Reference: N. Zuber, "Problems in Modeling of Small Break LOCA", NUREG-0724, 1980 INTRODUCTORY REMARKS 14

ICTP, 2007 A small digression on scaling laws… c) Imposing now equal elevations: (This condition is essential to keep equal gravity driving forces, i. e. in the case of Natural Circulation flows). Then, together with the Power to Volume relations, m SPECIFIES m as the ratio of cross sections. It also implies that velocities ARE equal. d) Furthermore, frictional effects are equal if: INTRODUCTORY REMARKS 15

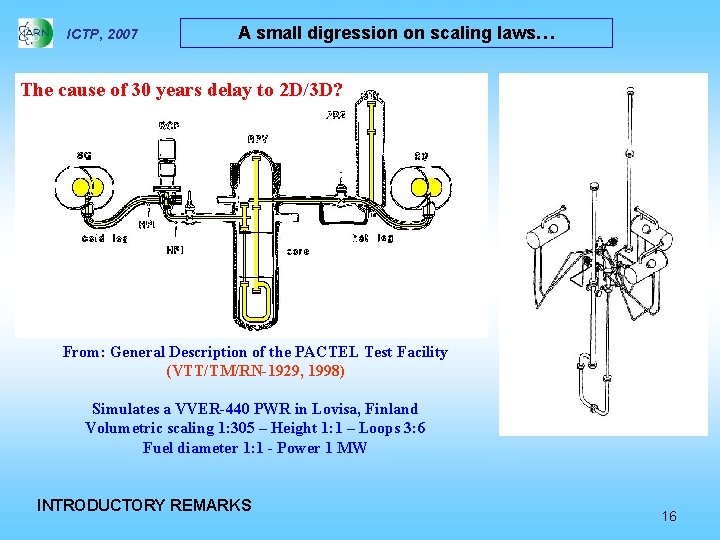
ICTP, 2007 A small digression on scaling laws… The cause of 30 years delay to 2 D/3 D? From: General Description of the PACTEL Test Facility (VTT/TM/RN-1929, 1998) Simulates a VVER-440 PWR in Lovisa, Finland Volumetric scaling 1: 305 – Height 1: 1 – Loops 3: 6 Fuel diameter 1: 1 - Power 1 MW INTRODUCTORY REMARKS 16

ICTP, 2007 A small digression on scaling laws… May be because (in my view). . . a) scaling laws “force” to almost 1 D integral representations of real life installations, with pre-established flow patterns b) a huge effort was focused on the development of a representative physical data base (amenable to 1 D analysis) and separate effects on the other side (like plume analysis, non-symmetric flow distribution, particular aspects of reactor components behavior, etc. ) affordable through detailed computational techniques c) code assessment for safety analysis also imposed a great effort for 1 D INTRODUCTORY REMARKS 17

ICTP, 2007 A small digression on scaling laws… . . . because (in my view). . . Cont´d. d) time scales to solve problems in realistic way (as a compromise between cell Courant number limitation for fast transients using semi-implicit methods and time inaccuracies, i. e. damping, for implicit methods) impose large number of time steps to span long time transients (e. g. in SBLOCAs) e) ill posedness of the governing equations “precluded” (for some people) search for detailed convergence of solutions, leading to coarse grid computations and stabilization of flow solvers by numerical means f) computers were not fast, cheap and widely available and not too many were interested in paying for detailed analyses, neither were asking too much for them… INTRODUCTORY REMARKS 18

ICTP, 2007 A small digression on scaling laws . . . because (in my view) Cont´d. “Sometimes, scaling leads to the adoption of the 1 -D approximation; this may, in turn, hide important aspects of the system physics. A simple example of this situation consists in keeping the height of the system unchanged to get the same buoyancy; then, if the system is scaled accordingly to the power/volume ratio, the cross section area of the volume will be reduced; this leads to a much smaller pipe diameter that makes the 1 -D representation reasonable, at the cost of eliminating the possibility of fluid internal recirculation” “A workaround for this situation is providing paths for recirculation, in the form of additional, interconnected components; however, this solution may impose the flow pattern in the system and the balance between these aspects is a challenge to any practitioner in natural circulation modeling” REFERENCE: On the analysis of thermal-fluid-dynamic instabilities via numerical discretization of conservation equations, J. C. Ferreri, W. Ambrosini, NED, 215, 153– 170, 2002 INTRODUCTORY REMARKS 19

ICTP, 2007 A small digression on scaling laws… However (I believe). . . 1 D, thermal hydraulics system codes will be used at least for a decade or more, coupled with 3 D modules for the core and/or for some specific components where separate effects analysis is the goal. Then, in the following slides, some basic aspects of numerical techniques as applied to simple 1 D problems of physical significance will be reviewed To start with, an exact, discrete approximation of a conservation like evolution equation will be developed INTRODUCTORY REMARKS 20

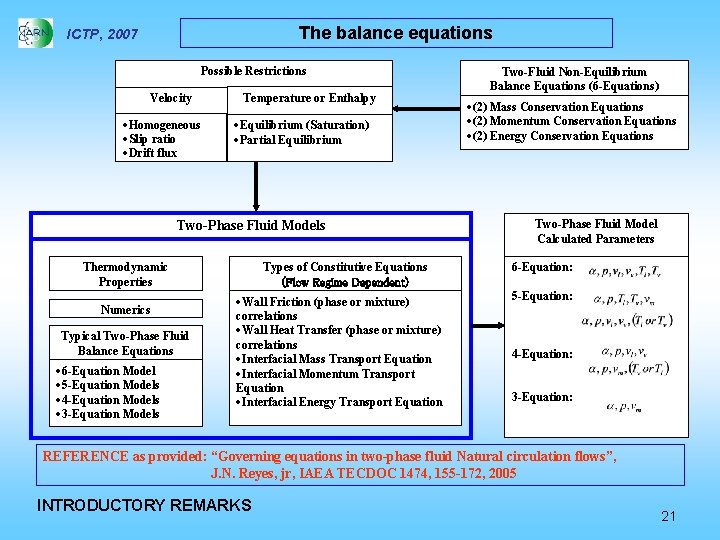
The balance equations ICTP, 2007 Possible Restrictions Velocity ·Homogeneous ·Slip ratio ·Drift flux Temperature or Enthalpy ·Equilibrium (Saturation) ·Partial Equilibrium Two-Phase Fluid Models Thermodynamic Properties Numerics Typical Two-Phase Fluid Balance Equations · 6 -Equation Model · 5 -Equation Models · 4 -Equation Models · 3 -Equation Models Types of Constitutive Equations (Flow Regime Dependent) ·Wall Friction (phase or mixture) correlations ·Wall Heat Transfer (phase or mixture) correlations ·Interfacial Mass Transport Equation ·Interfacial Momentum Transport Equation ·Interfacial Energy Transport Equation Two-Fluid Non-Equilibrium Balance Equations (6 -Equations) ·(2) Mass Conservation Equations ·(2) Momentum Conservation Equations ·(2) Energy Conservation Equations Two-Phase Fluid Model Calculated Parameters 6 -Equation: 5 -Equation: 4 -Equation: 3 -Equation: REFERENCE as provided: “Governing equations in two-phase fluid Natural circulation flows”, J. N. Reyes, jr, IAEA TECDOC 1474, 155 -172, 2005 INTRODUCTORY REMARKS 21

ICTP, 2007 Numerical approximations of conservation equations Let us consider the following evolution equation, depending on time t and space x, where L is a linear operator. u is the dependent variable. It may be expanded in Taylor series around t+ t Where HOT means terms of higher order. This equation may be formally written as: Which is an explicit approximation to the evolution differential equation ON NUMERICAL METHODS 22

ICTP, 2007 Numerical approximations of conservation equations By pre/post multiplying by suitable operators, implicit approximations may be obtained, like Crank Nicholson or fully implicit, as follows: If L is a 3 D operator, i. e. L = L 1 + L 2 + L 3, the corresponding fully implicit approximation is: ON NUMERICAL METHODS 23

ICTP, 2007 Numerical approximations of conservation equations Introducing intermediate definitions for u (they are not necessarily intermediate time approximations) then: That is a sequence of 1 D problems, known as an Aternating Direction Implicit method when L 1, L 2 and L 3 depend on each space coordinate. Now, the discrete approximation in space will be introduced. It is: ON NUMERICAL METHODS 24

ICTP, 2007 Numerical approximations of conservation equations Introducing a centered difference operator, defined as: Then, Finally: ON NUMERICAL METHODS 25

ICTP, 2007 Numerical approximations of conservation equations THE PREVIOUS EQUATION IS AN EXACT DISCRETE REPRESENTATION OF THE EVOLUTION EQUATION In this form it is not useful for working All practical approximation come from truncation of the series This, in turn, implies the appearance of the truncation error of the approximation. Postulate: TRUNCATION ERROR IS NOT A DISGRACE Its adequate treatment allows the construction of useful working techniques. ON NUMERICAL METHODS 26

ICTP, 2007 Three necessary definitions… CONSISTENCY Given a dependent variable that is sufficiently differentiable in a domain D and its boundary R, then, if an appropriate norm of the truncation errors L - Lh and B - Bh tend to zero when the increments of the independent variables tend to zero in some way, then the discrete scheme Lh, Bh is said consistent with the differential operators L, B STABILITY Given a function U defined in all the points of a grid in D and its boundary R, then, if exists a finite quantity K such that in an appropriate norm, it is for all the functions U defined in D+R, then the discrete scheme is said stable Consistency and Stability may be conditional ON NUMERICAL METHODS 27

ICTP, 2007 Three necessary definitions CONVERGENCE Given a function U defined in all the points P of a grid in D and its boundary R, then, considering linear operators, if the discrete scheme is consistent and stable, then the discrete scheme is convergent, i. e. : This is the equivalence theorem of P. Lax that allows constructing discrete, convergent solutions of a differential problem. ON NUMERICAL METHODS 28

ICTP, 2007 EXAMPLES Pure, 1 D diffusion equation: Truncating to O( t, x 2) it is: Finally, the 1 st order in time, Euler´s approximation is obtained: This scheme is conditionally stable ON NUMERICAL METHODS 29

ICTP, 2007 EXAMPLES Linear, 1 D scalar advection-diffusion equation Approximating by centered differences, it is: After expanding in Taylor series and keeping second order terms, it follows that: Reference: Heuristic Stability Theory for FDE, C. W. Hirt, J. Comp. Phys. , 2, pp. 339 -355, 1968 ON NUMERICAL METHODS 30

ICTP, 2007 EXAMPLES The previous expression is an hyperbolic differential equation and, in order that its domain of influence is to be contained in the domain of influence of the difference equation. A necessary condition is that: Coming back to the expanded difference equation and introducing the original differential equation, it follows that: The previous expression clearly imposes: ON NUMERICAL METHODS 31

ICTP, 2007 EXAMPLES Let us now consider the scalar advection equation, i. e. = 0 and consider the following approximation: Proceeding as above, it is: that is a parabolic equation. ON NUMERICAL METHODS 32

ICTP, 2007 EXAMPLES that leads to The expression above implies that the fluid can span at most a cell length in a time interval to keep calculation stable. The cell Courant number is defined as: and must be less (or equal to be strict) than unity. In advection dominated problems, it is usually taken as 0. 8 ON NUMERICAL METHODS 33

ICTP, 2007 EXAMPLES The non centered expression introduced is called an upwind approximation of the advection term and generates artificial or numerical diffusion that in the case of the transport of sharp waveforms or shock waves, smoothes the solution making it computable (the last concept was introduced by von Newman and Richtmyer in 1950) In conjunction with the explicit time approximation constitutes the “Forward time, upwind space” approximation to the scalar wave equation or FTUS method. This is the usual approximation used in the CFD codes to stabilize calculations or to regularize ill-posed models like in RELAP 5, through the introduction of numerical diffusion. Many other methods have been developed with this philosophy. Adequate discretization permits keeping low truncation error and allowing the computation of unstable flows. Reference: “A Method for the Numerical calculation of Hydrodynamic Shocks”, J. von Neumann and R. D. Richtmyer, J. Applied Phys. , 31, pp. 232 -237, 1950 ON NUMERICAL METHODS 34

ICTP, 2007 Managing truncation error to linearize governing eqns. It was asserted that truncation error is not a disgrace. In what follows this will be justified, simply by showing how use this concept to linearize Burger´s like operators. Let: be the equation under analysis, where L 1 is a linear operator and N is a nonlinear operator. Let us assume that N is restricted to the form: where L 2(u) is linear in u and A is such that the algebraic problem resulting from the discrete approximation of the previous equations is also linear. Burger's equation is a useful example; in this case: ON NUMERICAL METHODS 35

ICTP, 2007 Managing truncation error to linearize governing eqns. A Crank-Nicholson approximation may be written as: where I is the identity operator and A* is a matrix independent of time and a suitable approximation to A to be defined in what follows. Expanding this expression in a Taylor series around n, we get: ON NUMERICAL METHODS 36

ICTP, 2007 Managing truncation error to linearize governing eqns. Then, but, from the original equation: Then, it follows that: ON NUMERICAL METHODS 37

ICTP, 2007 Managing truncation error to linearize governing eqns. In order to obtain an estimation for we now ask: under which conditions is this equation an "exact", i. e. , an O( t 2) approximation to the solution of the original equation? The answer comes from subtracting the previous equation from the original one: This expression is equivalent to: Finally, after postmultiplying by and adopting we obtain the “exact” [i. e. O( t 2) ] solution. ON NUMERICAL METHODS 38

ICTP, 2007 Managing truncation error to linearize governing eqns. Because of the CN formulation, terms involving additional diffusion terms do not arise. If A* is evaluated as shown, the technique coincides with a predictor-corrector scheme based on the evaluation of "non-linear" coefficients evaluated at This result is well known. As may be observed from the above derivation, truncation error may be used, again, in a convenient way ON NUMERICAL METHODS 39

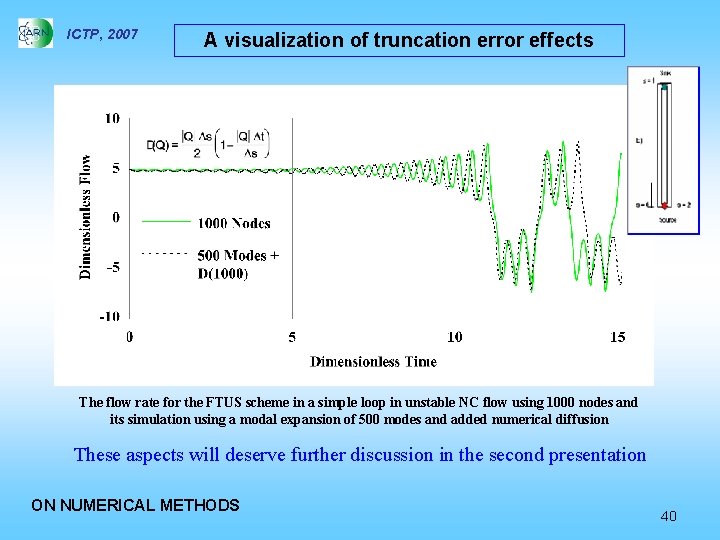
ICTP, 2007 A visualization of truncation error effects The flow rate for the FTUS scheme in a simple loop in unstable NC flow using 1000 nodes and its simulation using a modal expansion of 500 modes and added numerical diffusion These aspects will deserve further discussion in the second presentation ON NUMERICAL METHODS 40

ICTP, 2007 There is more than truncation error… 1/5 Group velocity governs the transport of energy when the governing equations are dispersive, i. e. equations that admit solutions of the form: but with the property that the speed of propagation of the waves are dependent of . In this expression is the wave number and is the angular wave frequency. If is the wave length, the resolution is defined as m= / x The group velocity is defined as: Additionally, by definition: = m REFERENCE: Group Velocity in Finite Difference Schemes, L. N. Threfethen, SIAM Review, 24, 113 -135, 1982 ON NUMERICAL METHODS 41

ICTP, 2007 There is more than truncation error… 2/5 It is obtained replacing by in the discrete equations each expression of U by: …as an example. and is a function of the resolution m and the cell Courant number CO The numerical scheme to illustrate this property is the LEAPFROG scheme, as applied to the linear scalar wave equation, one of the simplest numerical schemes, of order O(2, 2) and defined by: ON NUMERICAL METHODS 42

ICTP, 2007 There is more than truncation error… 3/5 Then: The illustration considers the LINEAR ADVECTION OF A SCALAR with two different wave forms, namely a smooth Gaussian and a wave packet. In both cases, the transport velocity is C = 1, the space interval is Δx = 1/160, the Courant number is CO = 0. 4, the resolution is m = 8 and the total time of integration is t = 2. With the above parameters, the group velocity is 0. 74 ON NUMERICAL METHODS 43

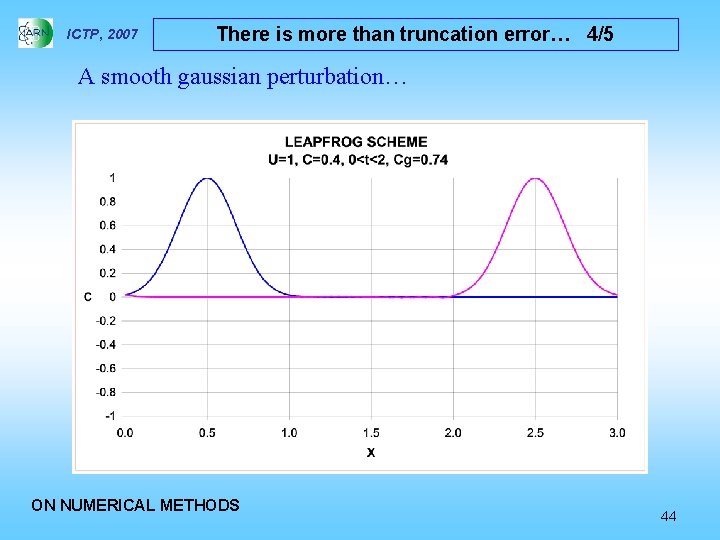
ICTP, 2007 There is more than truncation error… 4/5 A smooth gaussian perturbation… ON NUMERICAL METHODS 44

ICTP, 2007 There is more than truncation error… 5/5 A wave packet perturbation… ON NUMERICAL METHODS 45

ICTP, 2007 On using CFD for NC calculations Why it is worth considering CFD approaches for CN, even in simple cases… …through an example of how using well established, “natural” 1 D laws in 1 D TH loops to get non-conservative, wrong results Let us consider the NC flow in a simple TH loop in unstable flow conditions ON NUMERICAL METHODS 46

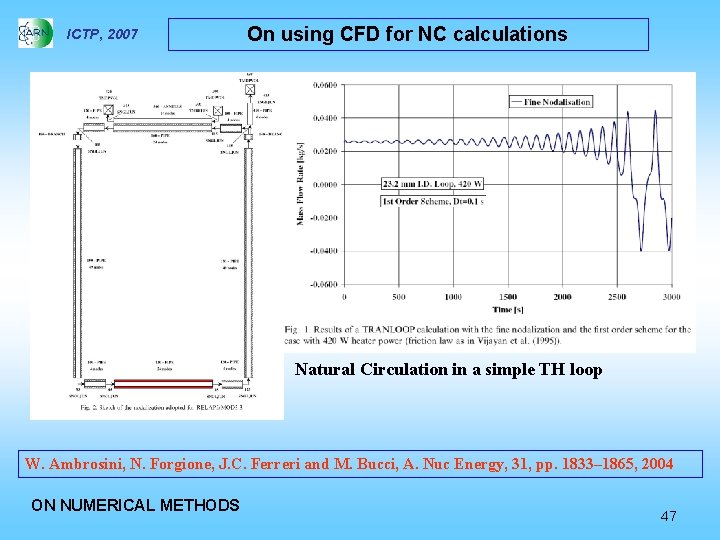
ICTP, 2007 On using CFD for NC calculations Natural Circulation in a simple TH loop W. Ambrosini, N. Forgione, J. C. Ferreri and M. Bucci, A. Nuc Energy, 31, pp. 1833– 1865, 2004 ON NUMERICAL METHODS 47

ICTP, 2007 ON NUMERICAL METHODS On using CFD for NC calculations 48

ICTP, 2007 ON NUMERICAL METHODS On using CFD for NC calculations 49

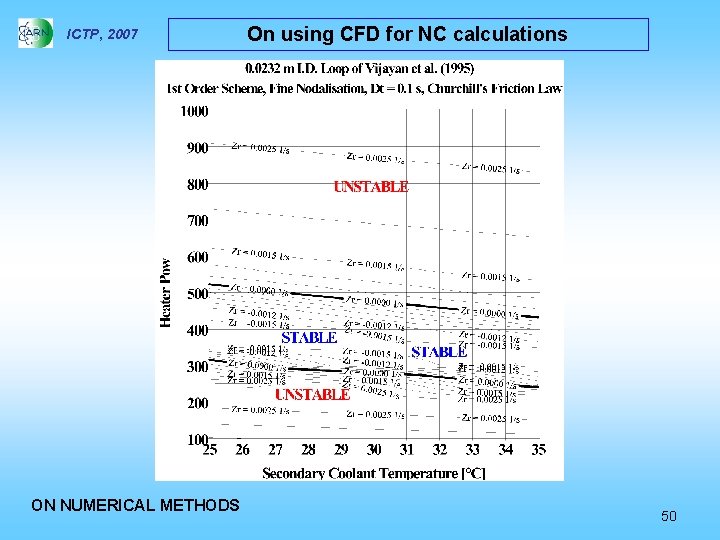
ICTP, 2007 ON NUMERICAL METHODS On using CFD for NC calculations 50

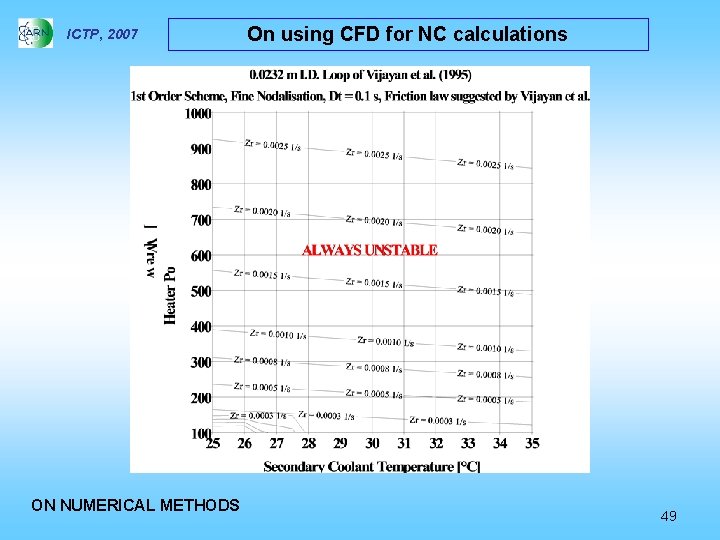
ICTP, 2007 On using CFD for NC calculations What if we go to a CFD approach for this simple problem? CODE: FLUENT 6. 0 CELL No. : about 50000 CPU time to span 1000 s: three days on a standard PC Using RELAP 5: CPU time to span 1000 s: some minutes on the same PC PS: no macroscopic friction law are used by FLUENT in this case. . . ON NUMERICAL METHODS 51

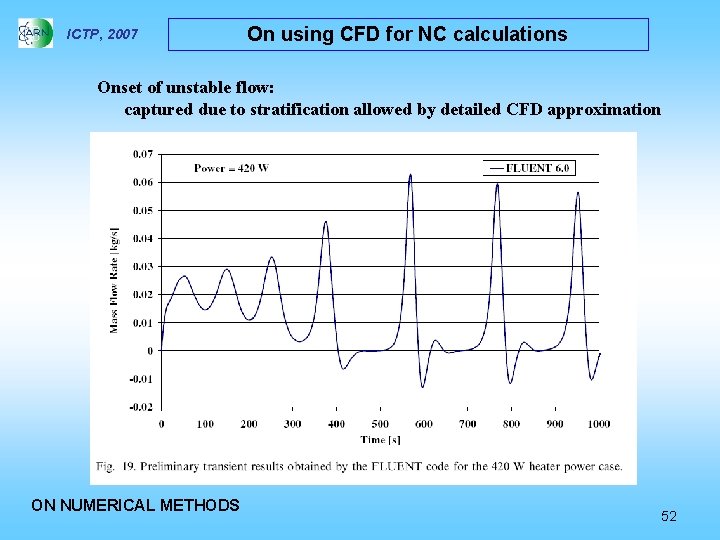
ICTP, 2007 On using CFD for NC calculations Onset of unstable flow: captured due to stratification allowed by detailed CFD approximation ON NUMERICAL METHODS 52

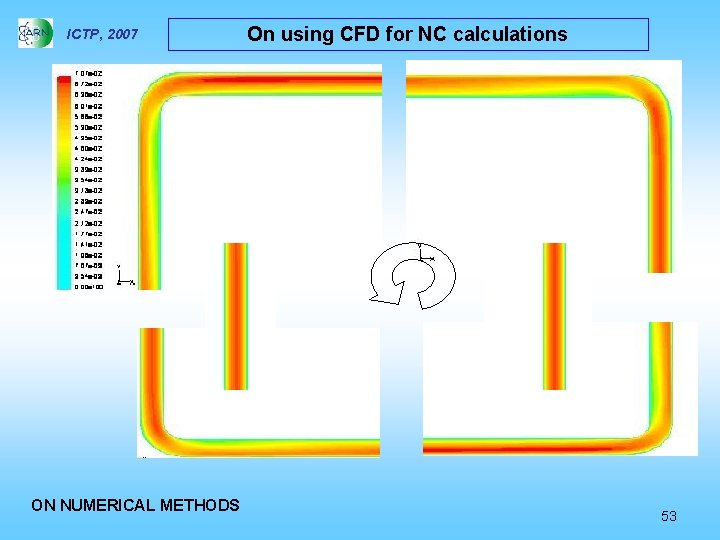
ICTP, 2007 ON NUMERICAL METHODS On using CFD for NC calculations 53

ICTP, 2007 On using CFD for NC calculations Some collaborative efforts to elucidate the needs on CFD in relation to Nuclear Safety evaluations Evaluation of CFD methods for reactor safety analysis - ECORA (12 partner institutions, see M. Scheuerer el al. , NED, vol. 235, pp. 359 -368, 2005) • To show to end-users, utilities and regulators to which extent CFD can enhance the accuracy of safety analysis implies “addressing the lack of certainty on CFD results and defining related Best Practice Guidelines to evaluate these results” ON THE PRESENT STATUS OF CFD IN RELATION TO NUCLEAR SAFETY 54

ICTP, 2007 On using CFD for NC calculations Objectives reached, according to authors: • The establishment of BPGs for ensuring high-quality results and for the formalized judgment of CFD calculations and experimental data. • The assessment of the potential, and of current limitations of CFD methods for flows in the primary system and in LWR containments, with special emphasis on PTS. • The definition of experimental requirements for the verification and validation of CFD software for flows in the primary system and in LWR containments. • The identification of improvements and extensions to the current CFD packages that are necessary for primary loop and containment flow analysis. • The implementation and validation of improved turbulence and two-phase flow models for the simulation of PTS phenomena in PWR primary systems. From M. Scheuerer el al. , NED, vol. 235, pp. 359 -368, 2005 ON THE PRESENT STATUS OF CFD IN RELATION TO NUCLEAR SAFETY 55

ICTP, 2007 On using CFD for NC calculations The BPGs are documented in Menter (2002). They contain detailed information on: • The formalized judgement of results obtained with different CFD software packages. This includes the definition and quantification of round-off, iteration, and discretisation errors, and the assessment of modelling errors. • The consistent use of CFD methods for reactor safety problems. These guidelines relate to geometry and grid generation, boundary and initial condition specification, selection of suitable physical models, and handling of solution algorithms. • The judgement of experiments regarding their use for verification and validation of CFD methods. The guidelines include criteria for checking global mass, momentum, and energy balances, consistency checks for field data, and plausibility checks. Experiments are grouped in a hierarchy ranging from laboratory studies to industrial field tests. The BPG report is intended as a living document. REFERENCE: M. Scheuerer el al. , NED, 235, pp. 359 -368, 2005 F. Menter, EVOL - ECORA - D 01, 2002 ON BEST PRACTICES AND OTHER ISSUES… 56

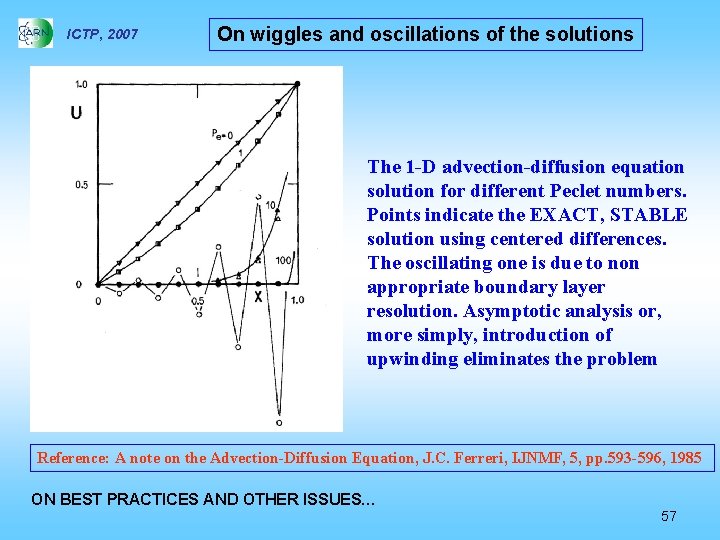
ICTP, 2007 On wiggles and oscillations of the solutions The 1 -D advection-diffusion equation solution for different Peclet numbers. Points indicate the EXACT, STABLE solution using centered differences. The oscillating one is due to non appropriate boundary layer resolution. Asymptotic analysis or, more simply, introduction of upwinding eliminates the problem Reference: A note on the Advection-Diffusion Equation, J. C. Ferreri, IJNMF, 5, pp. 593 -596, 1985 ON BEST PRACTICES AND OTHER ISSUES… 57

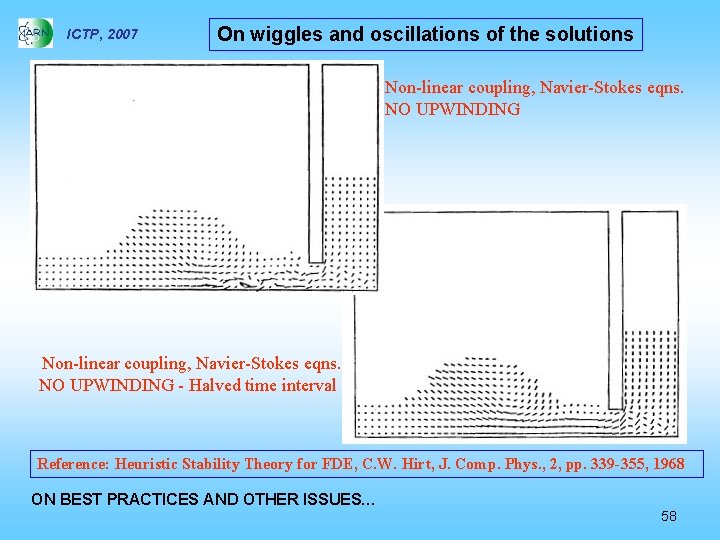
ICTP, 2007 On wiggles and oscillations of the solutions Non-linear coupling, Navier-Stokes eqns. NO UPWINDING - Halved time interval Reference: Heuristic Stability Theory for FDE, C. W. Hirt, J. Comp. Phys. , 2, pp. 339 -355, 1968 ON BEST PRACTICES AND OTHER ISSUES… 58

ICTP, 2007 On wiggles and oscillations of the solutions The existence of spurious oscillations in the solution of conservation equations may be the consequence of non appropriate resolution of the boundary layer behavior of the solution. Then, suppressing the oscillations may be non conservative or, equivalently, allow computing a solution not showing all the important aspects of the physics. Work done in the 80´s served to clarify this aspects. P. Gresho at the LLNL and at IJNMF contributed significantly to this subject. Reference: Don´t suppress the wiggles, they are telling you something, P. Gresho and R. Lee, Comp. and Fluids, 12, 223 -231, 1981 ON BEST PRACTICES AND OTHER ISSUES… 59

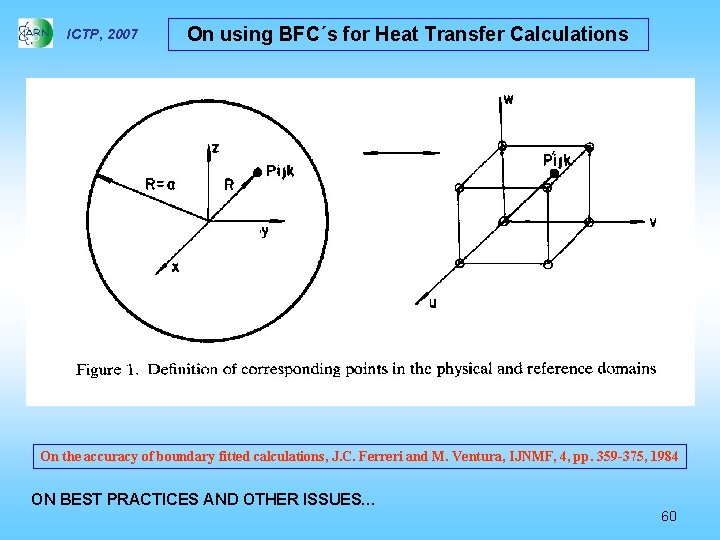
ICTP, 2007 On using BFC´s for Heat Transfer Calculations On the accuracy of boundary fitted calculations, J. C. Ferreri and M. Ventura, IJNMF, 4, pp. 359 -375, 1984 ON BEST PRACTICES AND OTHER ISSUES… 60

ICTP, 2007 On using BFC´s for Heat Transfer Calculations ON BEST PRACTICES AND OTHER ISSUES… 61

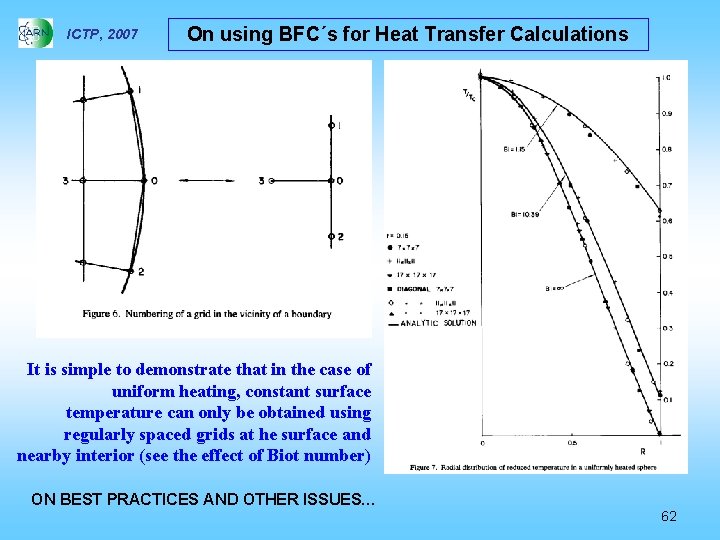
ICTP, 2007 On using BFC´s for Heat Transfer Calculations It is simple to demonstrate that in the case of uniform heating, constant surface temperature can only be obtained using regularly spaced grids at he surface and nearby interior (see the effect of Biot number) ON BEST PRACTICES AND OTHER ISSUES… 62

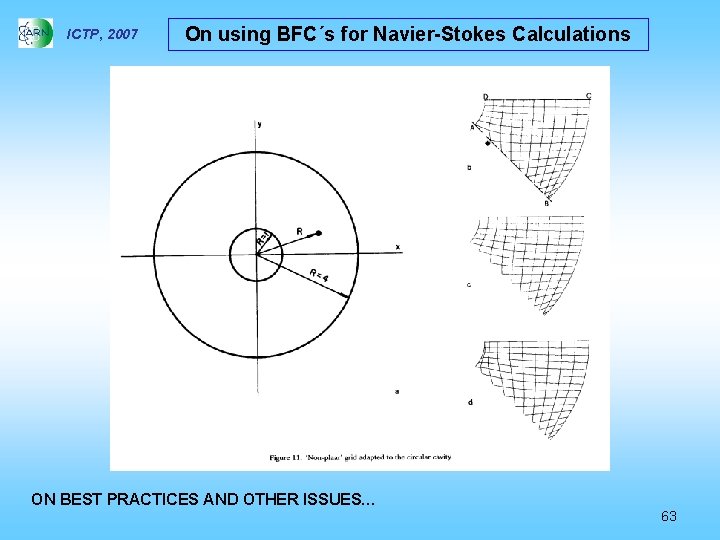
ICTP, 2007 On using BFC´s for Navier-Stokes Calculations ON BEST PRACTICES AND OTHER ISSUES… 63

ICTP, 2007 On using BFC´s for Navier-Stokes Calculations ON BEST PRACTICES AND OTHER ISSUES… 64

ICTP, 2007 Some preliminary conclusions… The use of adaptive grids must be exercised with care. Even 1 D cases may reflect the type of problems shown when the boundary conditions are of mixed (Robin) type. The use of norms to get an insight of convergence of the solution should also be applied with care, because the solution may be almost perfect, but delayed or advanced in time depending on the scheme and its group velocity. Oscillations in a computed solutions may be an indication of non appropriate discretization. Forcing its elimination may be a cause of losing information on the physics but, at the same time, making possible the calculation. ON BEST PRACTICES AND OTHER ISSUES… 65

ICTP, 2007 On using CFD for NC calculations Comments on BPGs • BPGs are a valuable contribution to freshmen • Evaluation of results validity beyond the known experimental data base range has always been one objective and an obvious difficulty of safety evaluations. Perhaps, whenever possible, designing SETs to interpolate should be a major goal to achieve • I do not believe too much in written best practice guides. Perhaps emphasizing on the need of a discipline of analysis in depth and to promote pursuing well founded Engineering Judgement at the Academia should be enough. Anyway, BPGs may be a way to consolidate Engineering Judgement traditions… PS: Ludwieg Prandtl (1875 -1953) was surprised to learn that people used to teach with books written by other authors. Then… ON BEST PRACTICES AND OTHER ISSUES… 66

ICTP, 2007 On using CFD for NC calculations Advanced computational tools are needed for, at least: • To implement further developments of existing physical models of two-phase flows, and the advanced, new ones proposed by the school of Ishii at Purdue and Lahey-Drew at RPI to deal with the smooth transitions in two-phase regimes, as opposed to fluid flow regime maps • To develop and implement 3 D, Two-Phase modules in commercial CFD software packages using friendly graphical user interfaces for the generation of grids and the visualization of results • To develop multiple-field, multiple-scale, multi-dimensional analysis tools • To verify and validate all the previously mentioned theories and implementations See also 1) Yadigaroglu et al. , NED, vol. 221, pp. 205 -223, 2003 on trends and needs in experimentation 2) Rohde et al. , NED, vol. 235, pp. 421 -443, 2005 on fluid mixing in the reactor circuit ON THE PRESENT STATUS OF CFD IN RELATION TO NUCLEAR SAFETY 67

ICTP, 2007 • • On using CFD for NC calculations The NEPTUNE Project was launched at the end of 2001 by EDF and CEA. The major underlying stakes for the nuclear industry partners are the competitiveness of the reactors and the safety of Nuclear Power Plants. The industrial situations which were identified as priority needs are all closely connected to these two major items Examples: 1. The improved prediction of Departure from Nucleate Boiling (DNB) ranks among the high priority needs since it is directly linked to fuel performance. 2. The estimation of the fluid temperature field on the Reactor Pressure Vessel (RPV) in case of a Pressurized Thermal Shock (PTS) for controlling the lifespan of critical components. 3. The prediction of the maximum cladding temperature during a Large. Break LOCA See Guelfi et al. , “A new multi-scale platform for advanced nuclear thermal-hydraulics status and prospects of the Neptune project”, NURETH 11, Avignon, France, 2005 ON THE PRESENT STATUS OF CFD IN RELATION TO NUCLEAR SAFETY 68

ICTP, 2007 On using CFD for NC calculations Next generation of flow solvers will be based on different scales of solution • “system” scale: dedicated to the overall description of the circuits of the reactor • “component” scale, often referred to as subchannel analysis or CFD in porous media • “CFD or CMFD (Computational Multi-Fluid Dynamics)” where the average scale is the millimeter or less “DNS” (Direct Numerical Simulation), where the characteristic length is less than the micrometer Guelfi et al. , NURETH 11, Avignon, France, October 2 -6, 2005, Contd. ON THE PRESENT STATUS OF CFD IN RELATION TO NUCLEAR SAFETY 69

ICTP, 2007 On using CFD for NC calculations Needs on numerical methods (models) • FEM and Finite Volume methods with unstructured meshes • Development of interface calculation and tracking • Domain decomposition to deal with computation of large scale simulations • Systematic application of discrete techniques in multiple thermodynamic conditions (incompressible – compressible, compression and rarefaction wave propagation, etc. ) • Proper treatment of interphase exchange • Smooth transitions for different two-phase flow conditions and enhanced two fluid models ON THE PRESENT STATUS OF CFD IN RELATION TO NUCLEAR SAFETY 70

ICTP, 2007 On using CFD for NC calculations On computers • PCs clusters allow considering very detailed nodalizations (up to 300 106 FEM 3 D elements grids are a –not too- common present practice with 200 PCs cluster) in the Computational Mechanics community. This allows computing the fluid flow distribution around a car in single-phase flow in a night • For a NPP, in a two loop geometry, 100 m 3 discretized at 1 cm 3 scale implies considering 100 106 elements. Then, steady state in single phase seems reachable within today computing possibilities if a multiple-scale method is used… By the way, the flow distribution at a SG inlet has been reported recently using 1 106 elements and FLUENT RECALL that this implies having verified and validated parallelized algorithms as well as models amenable to this treatment ON THE PRESENT STATUS OF CFD IN RELATION TO NUCLEAR SAFETY 71

ICTP, 2007 CONCLUSIONS • CFD is not a new activity in relation to NC and Nuclear Safety • The time to come will show an avalanche of papers dealing with separate effects, and multi field, multiple domain computational methods might provide a fertile ground for integral analysis • The experience gained in 25 years of using almost 1 D system codes and experimentation seems considered at present to specify needs in physical and numerical models • Collaborative efforts are under way for the benefit of the whole community • A discipline of analysis in depth and to promote well founded Engineering Judgement at the Academia would be worthwhile 72

ICTP, 2007 Thanks for attending and for your attention THE END 73