NUMERICAL METHODS FOR DIFFUSION EQUATION ON DISTORTED POLYHEDRAL

NUMERICAL METHODS FOR DIFFUSION EQUATION ON DISTORTED POLYHEDRAL MESHES Yuri Kuznetsov Department of Mathematics University of Houston http: //lacsi. rice. edu/review/2004/slides/Kuznetzov_LACSI_review. ppt

LACSI PROJECT: 2000 -2004 PARALLEL NUMERICAL METHODS FOR DIFFUSION EQUATIONS IN HETEROGENEOUS MEDIA ON STRONGLY DISTORED MESHES LANL: J. Morel, K. Lipnikov, M. Shashkov UH: Yu. Kuznetsov – PI O. Boyarkin, V. Gvozdev, D. Svyatskiy – graduate students S. Repin – visiting research professor

Outline Problem Formulation New Polyhedral Mesh Discretization Parallel Algebraic Solvers Applications and Numerical Results

Diffusion Equation Here

First Order Differential Equations p – pressure, density, intensity, or temperature u – flux vector function

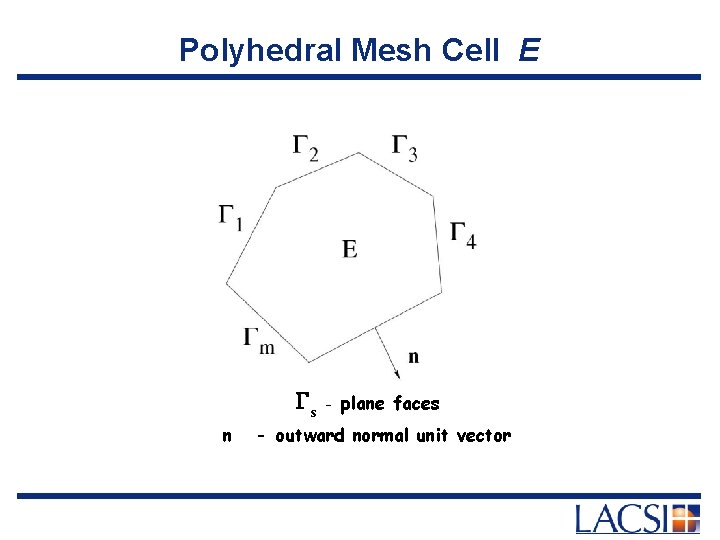
Polyhedral Meshes - polyhedral mesh cell - boundary of - interface between and

Polyhedral Mesh Cell E Gs n - plane faces - outward normal unit vector

Examples of E Pyramids Distored prisms

Examples of E Distored cubes Macro-Cell cluster of distorted prisms

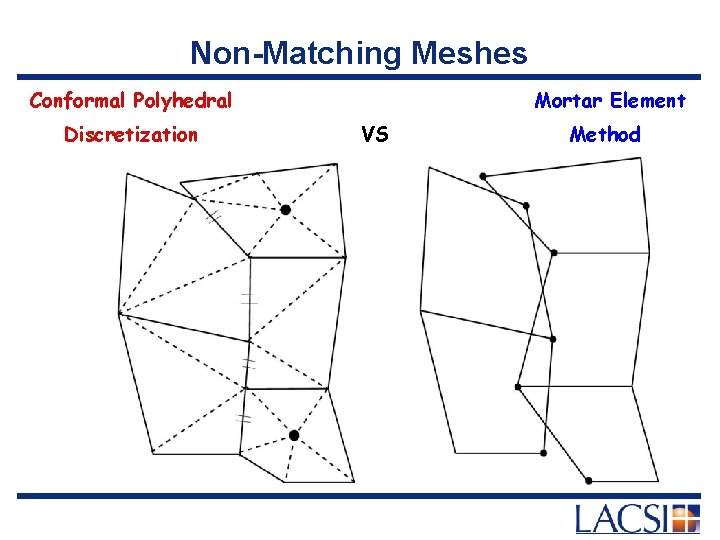
Non-Matching Meshes Conformal Polyhedral Discretization Mortar Element VS Method

Adaptive Mesh Refinement

Requirements For Discretization arbitrary polyhedral cells including nonconvex and degenerated ones arbitrary symmetric positive definite diffusion tensor one Degree of Freedom (DOF) per cell for the solution function one DOF per interface for the flux vector-function

Conservation Law Discrete conservation law where Remark: The discrete equation is exact

Major Problem to approximate the equation or the equivalent variational equation where v is a test vector function

Drawbacks of Existing Polyhedral Mesh Discretizations Mixed Finite Element (MFE) Method only tetrahedral meshes (classical variant) only distorted convex prismatic and cubic cells (variant with Piola Transformation) Finite Volume (FV) Method only convex polyhedrons very low accuracy on strongly distorted polyhedrons low accuracy for nonscalar diffusion tensor results in nonsymmetric matrices

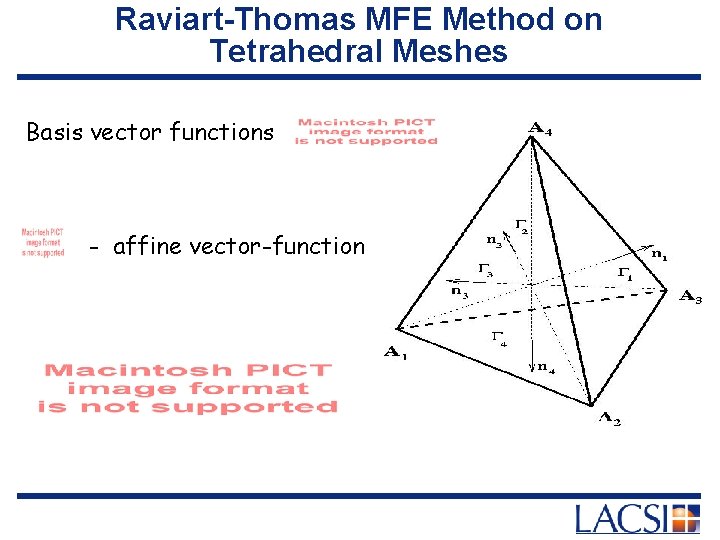
Raviart-Thomas MFE Method on Tetrahedral Meshes Basis vector functions - affine vector-function

Raviart-Thomas MFE Method on Tetrahedral Meshes Then by we get the discrete equations where

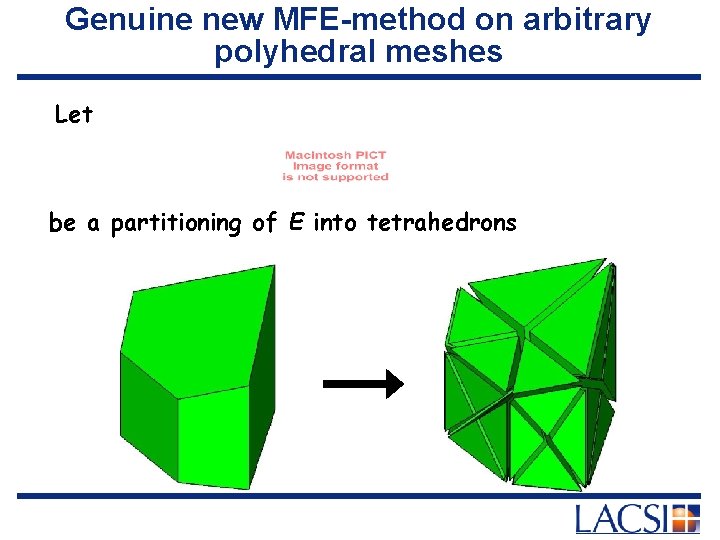
Genuine new MFE-method on arbitrary polyhedral meshes Let be a partitioning of E into tetrahedrons

Kuznetsov-Repin, 2003 To design the basis vector-functions we solve the local diffusion problem with the Neumann-type boundary conditions by the Raviart-Thomas MFE method on the tetrahedral mesh Here, is the positive constant.

Polyhedral Mimetic Finite Difference (MFD) Method Kuznetsov-Lipnikov-Shashkov: 2003 -2004 MFD-method mimics the most important properties of underlying physical and mechanical models, e. g. , conservation laws, as well as geometrical and mathematical symmetries. earlier versions did not allow nonconvex and degenerated polyhedrons

Numerical Experiments 1/h ep ef 4 2. 647 e-2 1. 330 e-1 8 9. 704 e-3 4. 587 e-2 16 2. 671 e-3 1. 233 e-2 32 6. 860 e-4 3. 155 e-3 1. 767 1. 808 Convergence rate

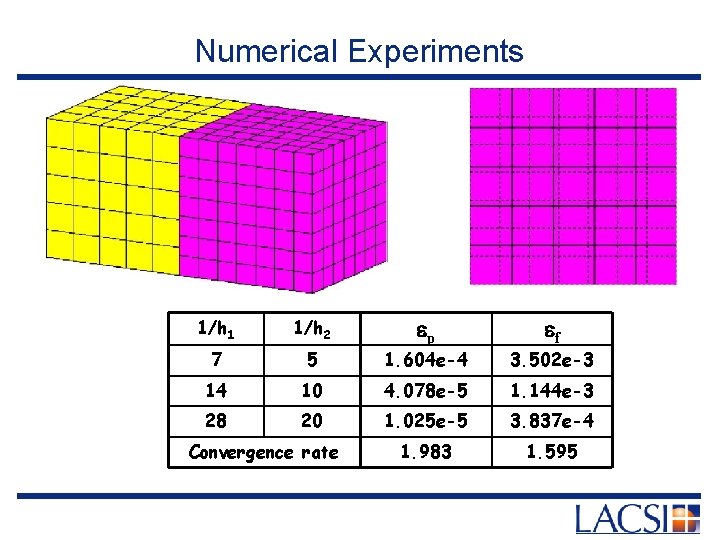
Numerical Experiments ep ef 1/h 1 1/h 2 7 5 1. 604 e-4 3. 502 e-3 14 10 4. 078 e-5 1. 144 e-3 28 20 1. 025 e-5 3. 837 e-4 1. 983 1. 595 Convergence rate

Advantages of the new method Arbitrary polyhedral meshes including meshes with nonconvex and degenerating cells Non-matching polyhedral meshes including AMR ones Arbitrary diffusion tensor Major restriction For accuracy reason the interface boundaries Gkl between different polyhedral cells Ek and El should be plane or "almost plane" polygons

Algebraic Problem

Condensed System Here -SPD matrix where -cell based matrices -assembling matrices

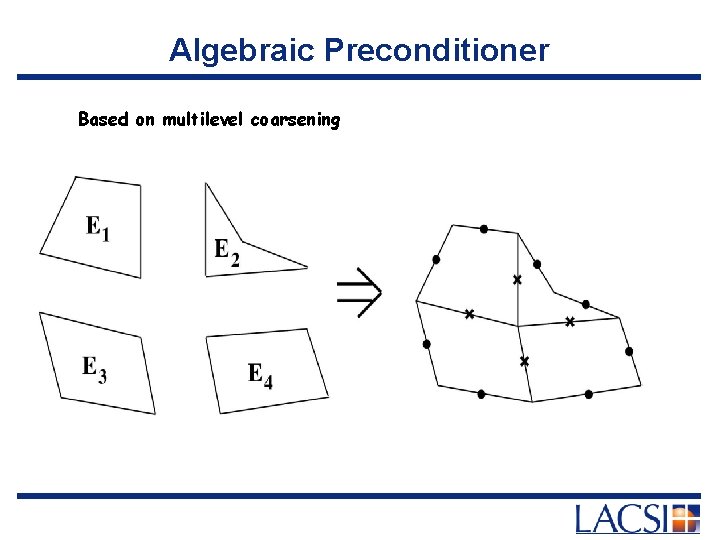
Algebraic Preconditioner Based on multilevel coarsening

DISTORTED 2 D-MESH

Preconditioned Conjugate Gradient Method • Stopping criterium: # of iterations Distortion factor q=0. 4 Distortion factor q=0. 3 128 x 128 256 x 256 512 x 512 Diagonal Preconditioner 227 455 882 Multilevel Preconditioner 21 25 29 128 x 128 256 x 256 512 x 512 Diagonal Preconditioner 262 483 967 Multilevel Preconditioner 21 26 30 Distortion factor q=0. 48 128 x 128 256 x 256 512 x 512 Diagonal Preconditioner 295 558 1106 Multilevel Preconditioner 21 27 30

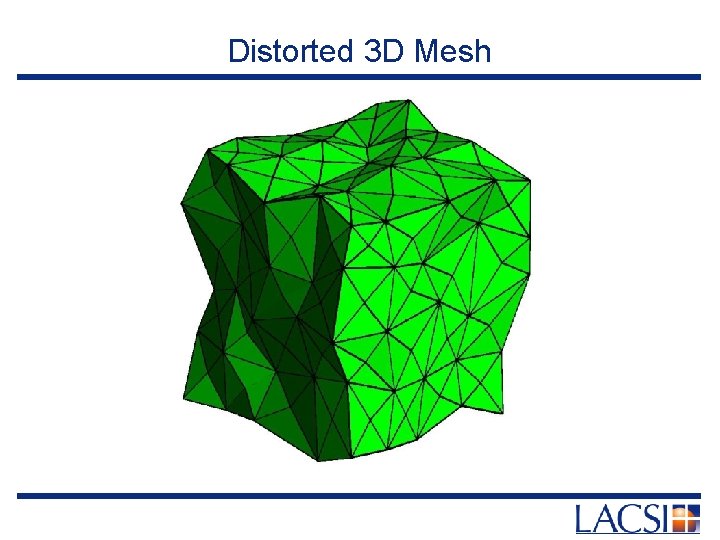
Distorted 3 D Mesh

Preconditioned Conjugate Gradient Method • Stopping criterium: # of iterations Distortion factor q=0. 0 16 x 16 32 x 32 Diagonal Preconditioner 78 153 Multilevel Preconditioner 27 28 Distortion factor q=0. 2 16 x 16 32 x 32 Diagonal Preconditioner 108 205 Multilevel Preconditioner 28 29 Distortion factor q=0. 3 16 x 16 32 x 32 Diagonal Preconditioner 130 223 Multilevel Preconditioner 29 30

ASC Relevant Application LANL researchers M. Shashkov and K. Lipnikov are now working with an X-3 team (S. Runnels) to implement the 3 D geometry version of the new polyhedral mesh discretization to model diffusion processes in Project B. The scheme currently existing is nonsymmetric. It is expected that the new scheme will be much more accurate, and it will cost far less to solve the underlying symmetric positive definite algebraic systems by Preconditioned Conjugate Gradient (PCG) method than the restarted GMRES method.

Other Applications Basin Modeling and Heat Transport in Strongly Heterogeneous Media on Highly Distorted Polyhedral Meshes (Exxon. Mobil Upstream Research Co. ) Numerical Simulation for Nuclear Waste Deposit (INRIA, France)

Joint Workshops LACSI Symposium 2003 Mimetic Methods for Radiation Transport and Diffusion (Yu. Kuznetsov, J. Morel, M. Shashkov) SIAM Conference on Mathematical and Computational Issues in Geosciences (Austin, 2003) Discretizations and Iterative Solvers for Diffusion Problems in Strongly Heterogeneous Media (Yu. Kuznetsov, M. Shashkov) LACSI Symposium 2004 Mimetic Methods for Partial Differential Equations and Applications (Yu. Kuznetsov, J. Morel, M. Shashkov)

EDUCATION ISSUES UH students on summer semesters at LANL 2001: K. Lipnikov, A. Hayrapetyan 2002: K. Lipnikov, V. Dyadechko 2003: V. Dyadechko 2004: D. Svyatskiy Ph. D. Thesis 2002: K. Lipnikov - currently a Post. Doc at T 7, LANL; considered for a tenure research position at LANL 2003: V. Dyadechko - currently a Post. Doc at T 7, LANL

List of Publications 1. M. Berndt, K. Lipnikov, D. Moulton, and M. Shashkov, Convergence of mimetic difference discretizations of the diffusion equations, J. Numer. Math. , 9 (2001), pp. 265 --284. 2. Yu. Kuznetsov and K. Lipnikov, Fast separable solvers for mixed finite element methods and applications, J. Numer. Math. , 10 (2002), pp. 137 --155. 3. Yu. Kuznetsov, Spectrally equivalent preconditioners for mixed hybrid discretizations of diffusion equations on distorted meshes, J. Numer. Math. , 11 (2003), pp. 61 --74. 4. Yu. Kuznetsov and S. Repin, New mixed finite element method on polygonal and polyhedral meshes, RJNAMM, 18 (2003), pp. 261 --278. 5. Yu. Kuznetsov and S. Repin, Mixed finite element methods on polygonal and polyhedral meshes, Proc. of the 5 th ENUMATH Conference, Prague, 2003. World Scientific Publ. Co. , 2004. 6. Yu. Kuznetsov, K. Lipnikov, and M. Shashkov, Mimetic finite difference equations on polygonal meshes for diffusion-type equations, Comput. Geosciences, 6 (2005).

Current and Further Research 1. Adaptive Refinement for Polyhedral Meshes 2. Parallel Algebraic Solvers 3. Polyhedral Discretizations for Radiation Transport Equations 4. Maxwell Equations on Polyhedral Meshes