Numerical Matrix methods for solving the System of







![Crammer’s Rule • [2] A textbook of Engineering Mathematics, Laxmi Publications, 173, eighth edition, Crammer’s Rule • [2] A textbook of Engineering Mathematics, Laxmi Publications, 173, eighth edition,](https://slidetodoc.com/presentation_image_h/b6aa761871279db6391a3da94a7e26f0/image-8.jpg)

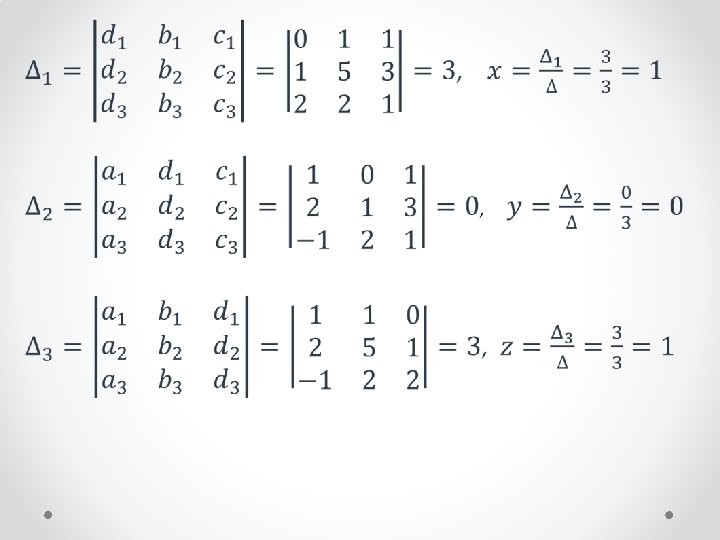






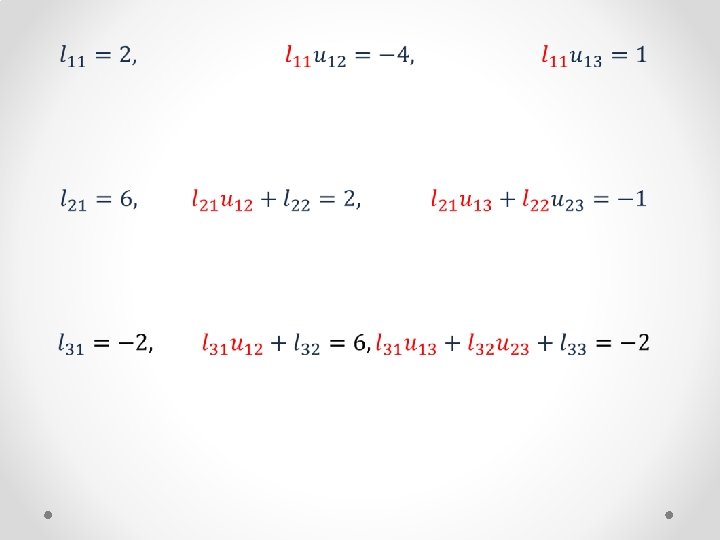






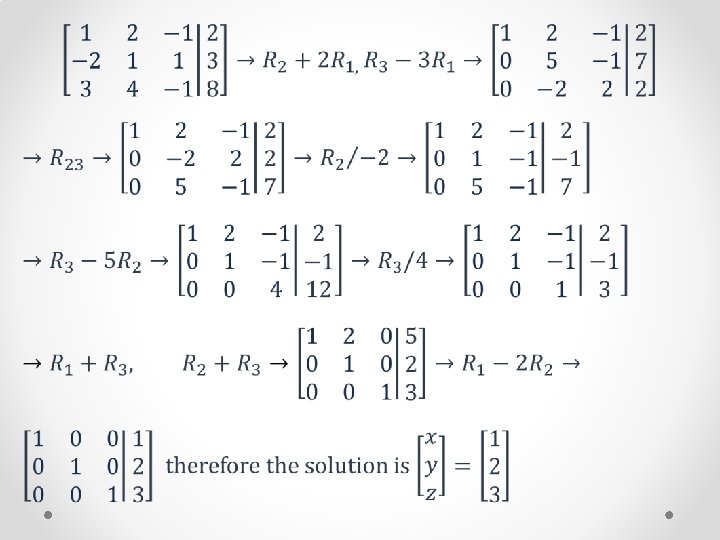





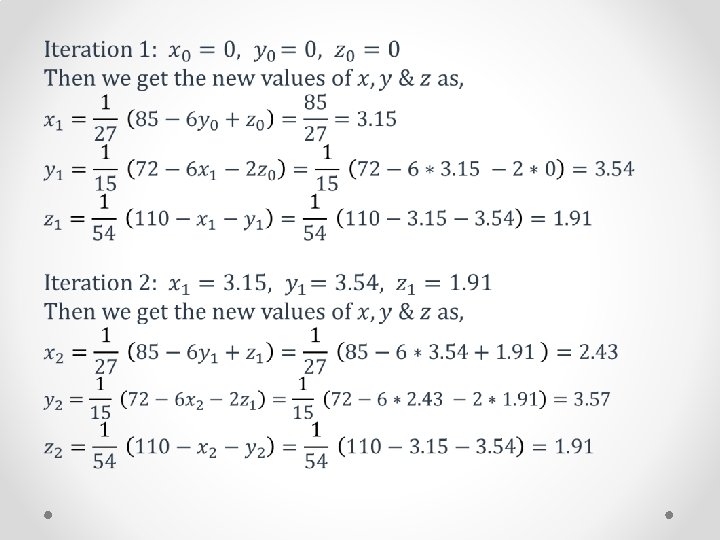


- Slides: 32

Numerical Matrix methods for solving the System of Linear algebraic equations By Poonam Deshpande Team 5 - RC 1229 This work is licensed under the Creative Commons Attribution. Share. Alike 4. 0 International License. To view a copy of this license, visit http: //creativecommons. org/licenses/by-sa/4. 0/ or send a letter to Creative Commons, PO Box 1866, Mountain View, CA 94042, USA.

Pre-requisites for this topic Students should have the knowledge of • Definition of a Matrix • Different types of matrices • Elementary transformations & determinant of Matrix • Matrix algebra like addition, subtraction and multiplication of matrices • System of Linear Algebraic Equations

Learning Objectives: Objectives • To understand how to solve the System of Linear Algebraic Equations in the matrix equation form using numerical matrix methods • To understand how to write a programing code for these matrix methods • To master the numerical methods like Crammer’s rule, Gauss-Jordan method, Crout’s Method, and Gauss-Seidel Method for solving the System of Linear Algebraic Equations • To develop the analytical ability to apply these learnings to the real world problems

Learning Outcomes • Students will be able to understand how to write a System of Linear Algebraic Equations in the matrix equation form • Students will be able to understand master the numerical methods like Crammer’s Rule, Gauss-Jordan method, Crout’s Method and Gauss-Seidel Method for solving the large System of Linear Algebraic Equations • Students will be able to write a programing code for these matrix methods • Students will develop the analytical ability to apply these learnings to the real world problems

System of linear algebraic equations •

Numerical Matrix methods • Crammer’s Rule • Gauss-Jordan Method • Crout’s Method • Gauss-Seidel method

Crammer’s Rule •
![Crammers Rule 2 A textbook of Engineering Mathematics Laxmi Publications 173 eighth edition Crammer’s Rule • [2] A textbook of Engineering Mathematics, Laxmi Publications, 173, eighth edition,](https://slidetodoc.com/presentation_image_h/b6aa761871279db6391a3da94a7e26f0/image-8.jpg)
Crammer’s Rule • [2] A textbook of Engineering Mathematics, Laxmi Publications, 173, eighth edition, 2011

Example •
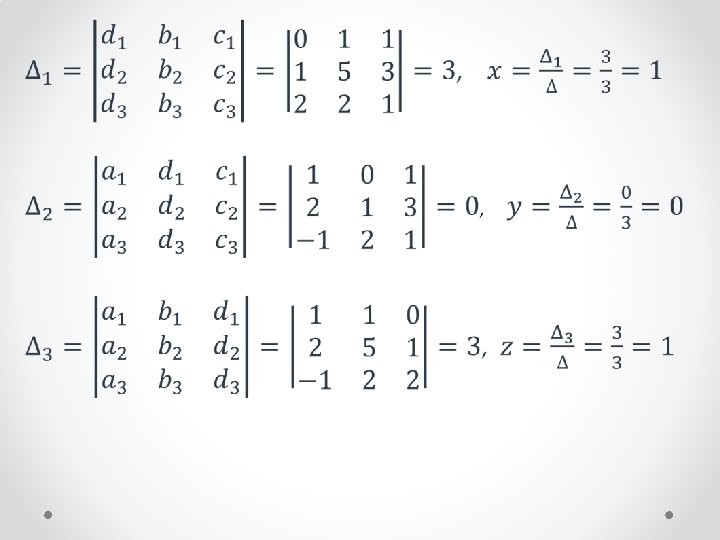

Crout’s Method •

Crout’s Method (cont. ) (1) (2) (3) (4) Therefore to find the solution of the system (1) we will have to solve (4) and then (3), but before that we will have to evaluate the values of L and U

Algorithm for Crout’s Method •

Algorithm for Crout’s Method (cont. ) •

Thank You

Example •
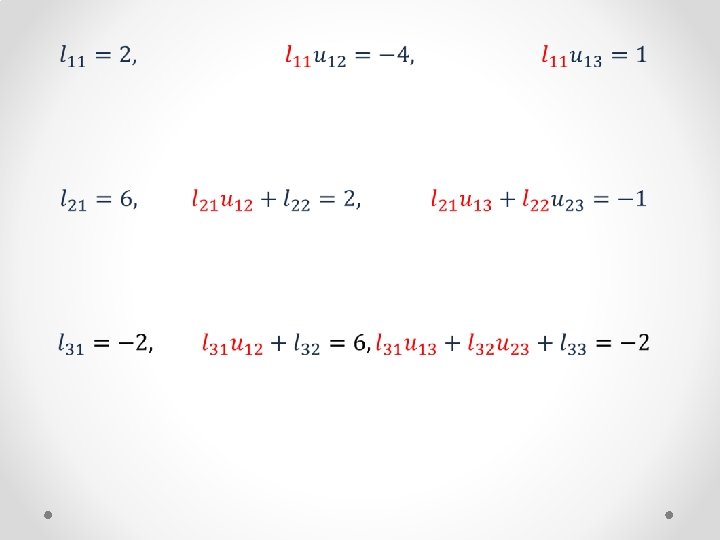


MOODLE Login • Use the following User-id and Password for accessing more practice questions and quizzes on MOODLE • • 1. MOODLE link https: //madaboutmathematics. moodlecloud. com/ 2. User-id=Student 3. Password= Student 1@

Thank You

Gauss-Jordan Method •

Gauss-Jordan Method(cont. ) •

Example •
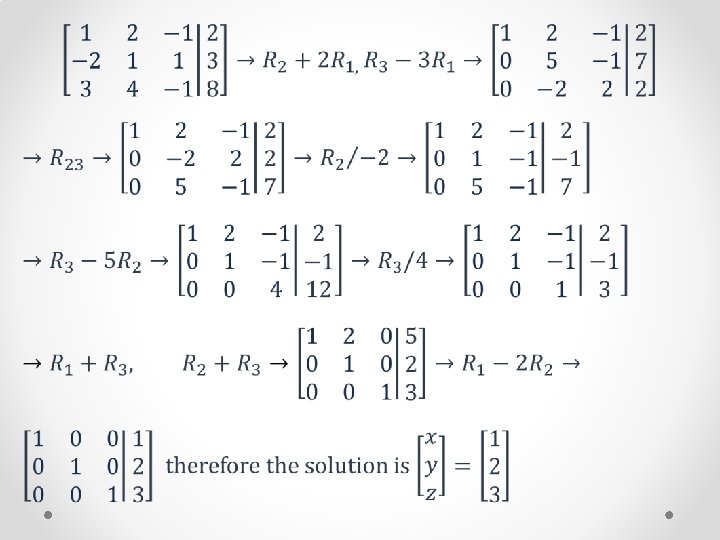

Gauss-Seidel Method •

Gauss-Seidel Method (cont. ) •

Gauss-Seidel Method (cont. ) •

Gauss-Seidel Method (cont. ) •

Gauss-Seidel method Example •
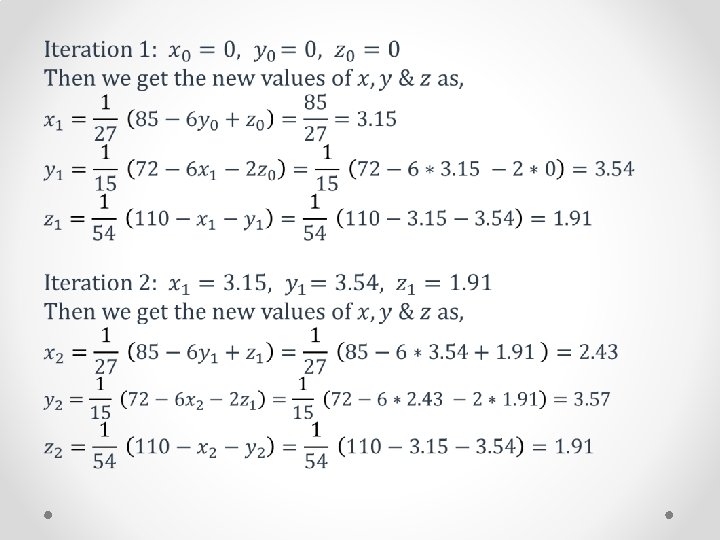


Thank You