Numerical Integration CSE 245 Lecture Notes Content n






















- Slides: 23

Numerical Integration CSE 245 Lecture Notes

Content n n Introduction Linear Multistep Formulae Local Error and The Order of Integration Time Domain Solution of Linear Networks

Introduction n n Transient analysis is to obtain the transient response of the circuits. Equations for transient analysis are usually differential equations. Numerical integration: calculate the approximate solutions Xn. Linear multistep formulae are the primary numerical integration method.

Linear Multistep Formulae n n Differential equations are X = F(X) Assume values Xn-1, Xn-2, … , Xn-k and derivatives X n-1, X n-2, … , X n-k are known, the solution Xn and X n can be approximated by a polynomial of these values: k k i=0 i. Xn-i + h i. X n-i = 0

Linear Multistep Formulae n Ø Ø There are two distinct classes LMS: Explicit predictors --- 0 = 0 --- Xn is the only unknown variable Implicit --- 0 0 --- Xn, X n are all unknown variables.

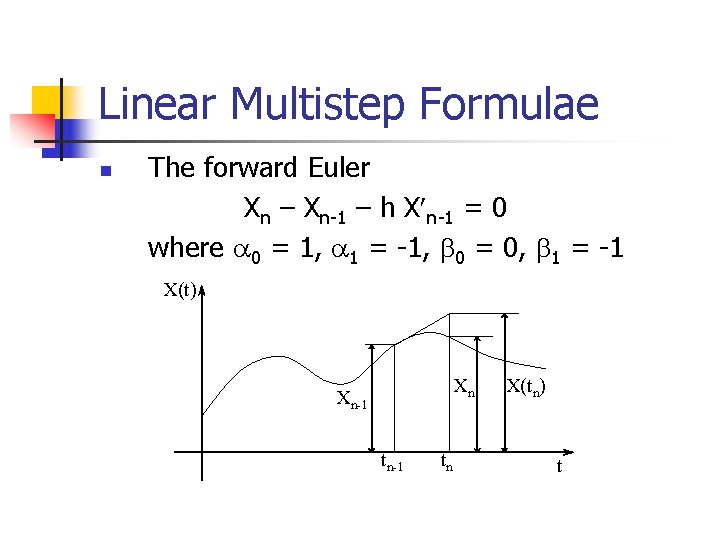
Linear Multistep Formulae n Ø Ø Ø Three simplest LMS formulae: The forward Euler The backward Euler Trapezoidal

Linear Multistep Formulae n The forward Euler Xn – Xn-1 – h X n-1 = 0 where 0 = 1, 1 = -1, 0 = 0, 1 = -1 X(t) Xn Xn-1 tn X(tn) t

Linear Multistep Formulae n n The backward Euler Xn – Xn-1 – h X n = 0 where 0 = 1, 1 = -1, 0 = -1, 1 = 0 It is an implicit representation. We may assume some initial value for Xn and iterate to approximate the solution Xn and X n.

Linear Multistep Formulae n Trapezoidal Xn – Xn-1 – h (X n + X n-1 )/2= 0 where 0 = 1, 1 = -1, 0 = -1/2, 1 = -1/2 n It is also an implicit representation. Xn, X n can be obtained through some iterative procedure.

Local Error n Ø Ø Two crucial concepts Local error --- the error introduced in a single step of the integration routine. Global error--- the overall error caused by repeated application of the integration formula.

Local Error X(t) Diverging flow Converging flow t Global error and local error

Local Error n Ø Ø Two types of error in each step: Round-off error --- due to the finiteprecision (floating-point) arithmetic. Truncation error --- caused by truncation of the infinite Taylor series, present even with infinite-precision arithmetic.

Local Error and Order of Integration n Local error Ek for LMS k k i=1 i=0 Ek = X(tn) + i. X(tn-i) + h i. X (tn-i) n Ek can be expanded into Taylor series. If the coefficients of the first pth derivatives are zero, the order of integration is p.

Order of Integration n Let X(t) = ((tn-t)/h)l and tn – tn-i = ih, n n k k i=0 Ek = i((tn-tn-i)/h)l + h (-l/h) i ((tn-tn-i)/h)l-1 For pth order integration, the first p+1 elements (l = 0, 1, … , p) will all be zeros: k n l = 0 n l = 1 n … n l = p i = 0 i=0 k ( ii - i) = 0 i=0 k [( ii - p i)ip-1] = 0 i=0

Order of Integration n The forward Euler 0 = 1, 1 = -1, 0 = 0, 1 = -1 So l = 0 l = 1 l = 2 0 + 1 = 1 + (-1) = 0; 0 0 + 1 1 - 0 - 1 = 1 0 + (-1) 1 - 0 – (-1) = 0; ( 1 1 - 2 1) 1 = ((-1) 1 - 2 (-1)) 1 = 1 0; The forward Euler is 1 th order.

Order of Integration n The backward Euler 0 = 1, 1 = -1, 0 = -1, 1 = 0 So l = 0 l = 1 l = 2 0 + 1 = 1 + (-1) = 0; 0 0 + 1 1 - 0 - 1 = 1 0 + (-1) 1 - (-1) - 0 = 0; ( 1 1 - 2 1) 1 = ((-1) 1 - 2 0) 1 = -1 0; The backward Euler is 1 th order.

Order of Integration n Trapezoidal 0 = 1, 1 = -1, 0 = -1/2, 1 = -1/2 So l = 0 l = 1 l = 2 l = 3 0 + 1 = 1 + (-1) = 0; 0 0 + 1 1 - 0 - 1 = 1 0 + (-1) 1 - (-1/2) – (-1/2) = 0; ( 1 1 - 2 1) 1 = ((-1) 1 - 2 (-1/2)) 1 = 0; ( 1 1 - 3 1) 12 = ((-1) 1 - 3 (-1/2)) 1 = 1/2 0; The trapezoidal method is 2 th order

Order of Integration The algorithm for defining and : --- Choose p, the order of the numerical integration method needed; --- Choose k, the number of previous values needed; --- Write down the (p+1) equations of pth order accuracy; --- Choose other (2 k-p) constrains of the coefficients and ; --- Combine and solve above (2 k+1) equations; --- Get the result coefficients and . n

Solution of Linear Networks n Combine the differential equations for linear networks and the numerical integration equations: k k i=0 i. Xn-i + h i. X n-i = 0 MX = -GX + Pu (1) (2)

Solution of Linear Networks (1) k k Xn + h 0 X n + i. Xn-i + h i. X n-i = 0 i=1 Xn + h 0 X n + b = 0 (3) X n = (-1/h 0)( Xn + b) (2)+(3) M[(-1/h 0)( Xn + b)] = -GXn + Pu (-1/h 0) Xn = -GXn + Pu + (M/h 0)b

Solution of Linear Networks n For capacitance C v c = ic C [(-1/h 0)( vc + bc)] = ic (-C/h 0) vc – (C/h 0) bc = ic ic ic vc – (C/h 0) bc (-C/h 0) vc

Solution of Linear Networks n For inductance L i l = vl L [(-1/h 0)( il + bl)] = vl (-L/h 0) il – (L/h 0) bl = vl il il vl vl +- – (L/h 0) bl (-L/h 0)

References n n CK. Cheng, John Lillis, Shen Lin and Norman Chang “Interconnect Analysis and Synthesis”, Wiley and Sons, 2000 Jiri Vlach and Kishore Singhal “Computer Methods for Circuit Analysis and Design”, 1983