Numerical Integration Approximating an integral by a sum

Numerical Integration: Approximating an integral by a sum
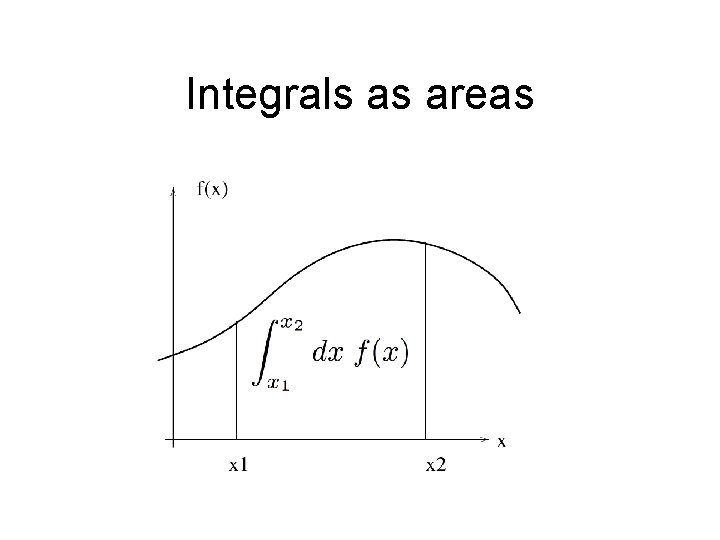
Integrals as areas
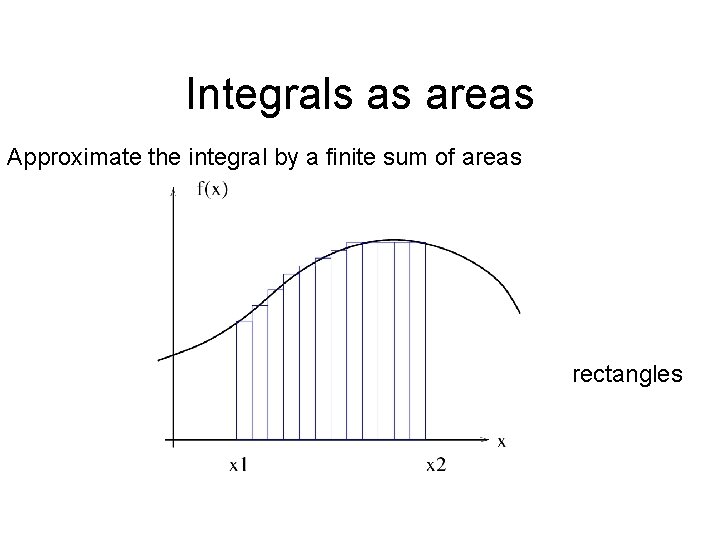
Integrals as areas Approximate the integral by a finite sum of areas rectangles
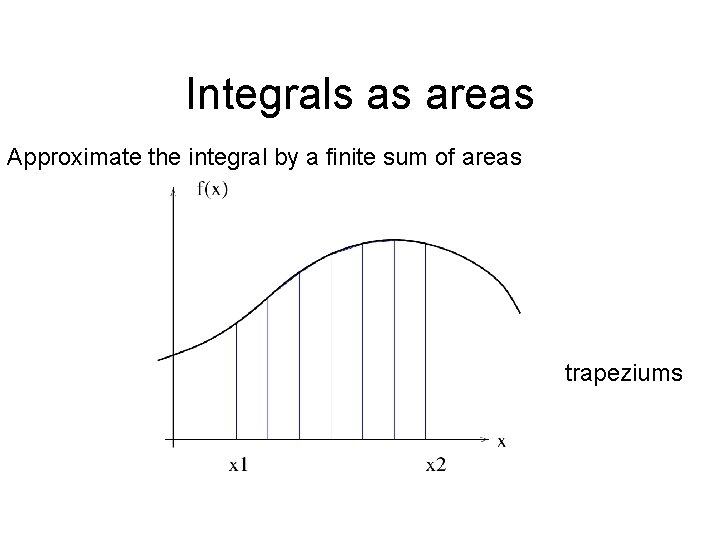
Integrals as areas Approximate the integral by a finite sum of areas trapeziums

Integrals as areas Trapezium rule: Associated error:

Integrals as areas Composite trapezium rule:

Integrals as areas Simpson’s rule:

Integrals as areas • the rectangle approximation takes the function to be constant in the interval • the trapezium rule uses linear interpolation between points • Simpson’s rule uses polynomial (quadratic) interpolation between the points and has an associated error • these should be compared to a Taylor expansion, the first term is a constant, the second term is linear, the third is quadratic…

Simpson’s rule: derivation by method of undetermined coefficients • express the integral as • this must hold for polynomials of degree two or less. • In particular, it must hold for • but we already know the left hand side for these

Simpson’s rule: derivation by method of undetermined coefficients Now calculate the right-hand-side: Solving these gives

Romberg integration: integration by iteration • make repeated use of the trapezium rule etc. • this is equivalent to etc. • this gives a series of approximations which can be used to extrapolate to give the answer

Romberg integration: doing the extrapolation • the algorithm takes the form of a triangle, Rjk, where we start with R 00 and work down R 00 R 11 R 20 R 21 R 22 R 30 R 31 R 32 R 33 … … are the approximations, repeat until

Romberg integration: doing the extrapolation The left hand column are given by the trapezium rule starting with To work from the left to the right for a given column use
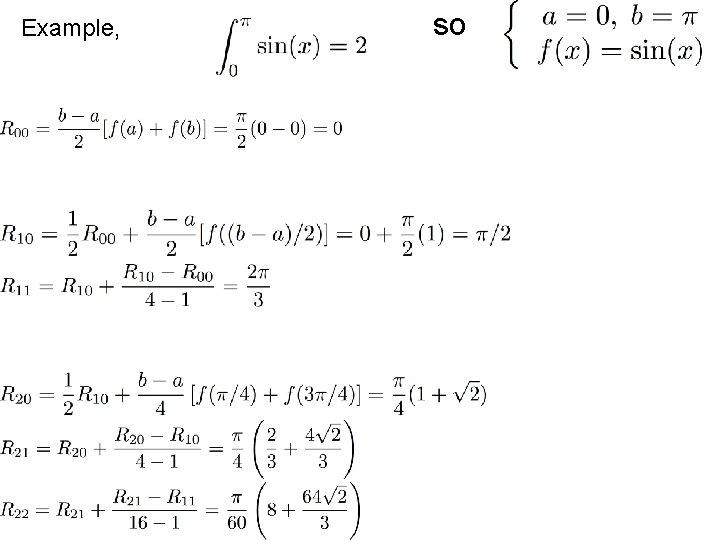
Example, so
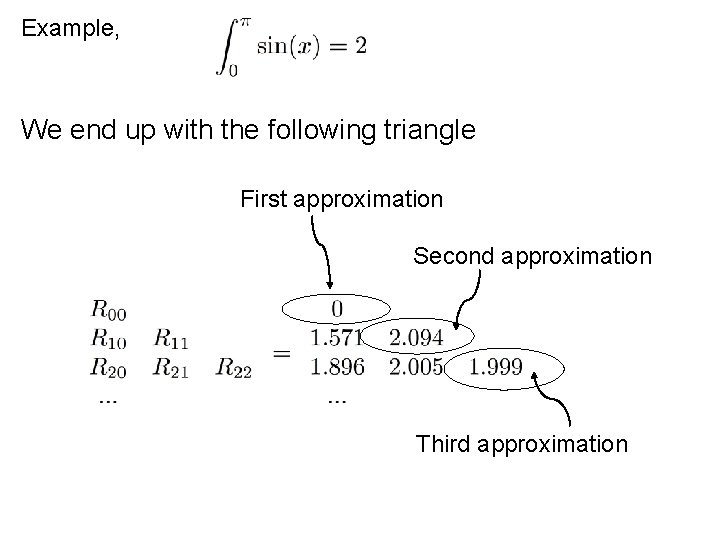
Example, We end up with the following triangle First approximation Second approximation Third approximation

Infinite ranged integrals: • evaluate an integral over an infinite range • the previous methods would lead to an infinite sum so cannot be used • transform the integral into a finite ranged integral, e. g. • change the variable in the second integral (prove this)
- Slides: 16