Numerical geometry of nonrigid shapes Partial similarity 1





















- Slides: 41

Numerical geometry of non-rigid shapes Partial similarity 1 Partial similarity © Alexander & Michael Bronstein, 2006 -2009 © Michael Bronstein, 2010 tosca. cs. technion. ac. il/book 048921 Advanced topics in vision Processing and Analysis of Geometric Shapes EE Technion, Spring 2010

Numerical geometry of non-rigid shapes Partial similarity Greek mythology 2

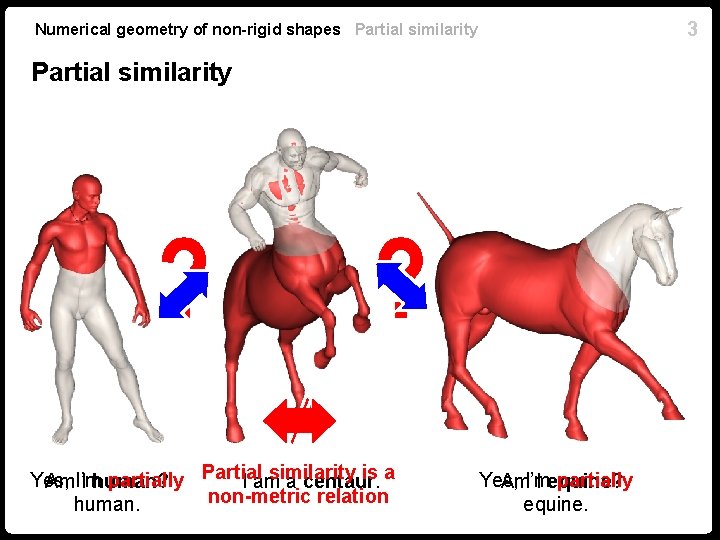
3 Numerical geometry of non-rigid shapes Partial similarity is a Yes, partially Partial Am. I’m I human? I am a centaur. non-metric relation human. Yes, partially Am. I’m I equine? equine.

Numerical geometry of non-rigid shapes Partial similarity Human vision example ? 4

5 Numerical geometry of non-rigid shapes Partial similarity Visual agnosia Oliver Sacks The man who mistook his wife for a hat

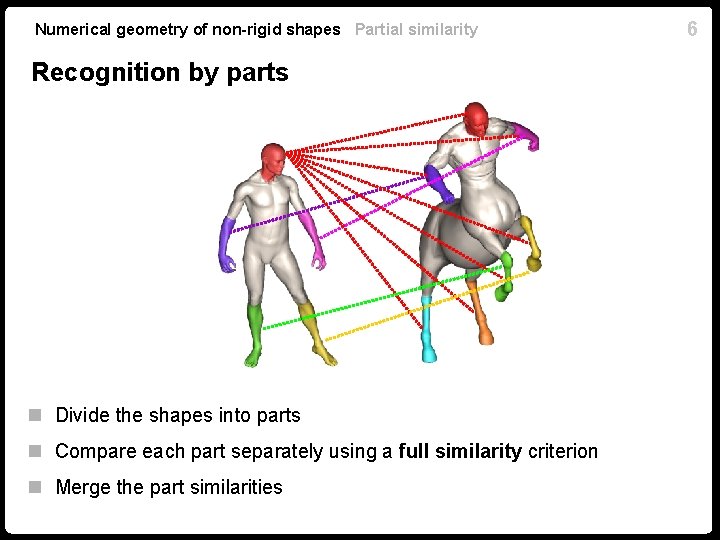
Numerical geometry of non-rigid shapes Partial similarity Recognition by parts n Divide the shapes into parts n Compare each part separately using a full similarity criterion n Merge the part similarities 6

Numerical geometry of non-rigid shapes Partial similarity X and Y are partially similar = X and Y have significant similar parts Illustration: Herluf Bidstrup 7

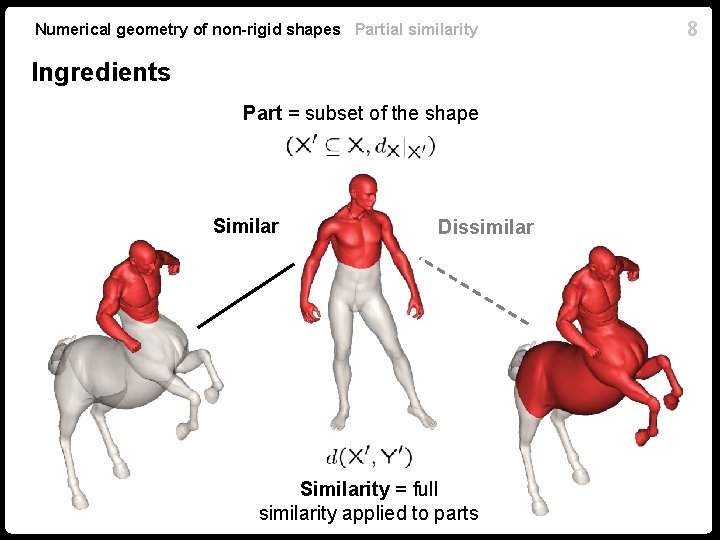
Numerical geometry of non-rigid shapes Partial similarity Ingredients Part = subset of the shape Similar Dissimilar Similarity = full similarity applied to parts 8

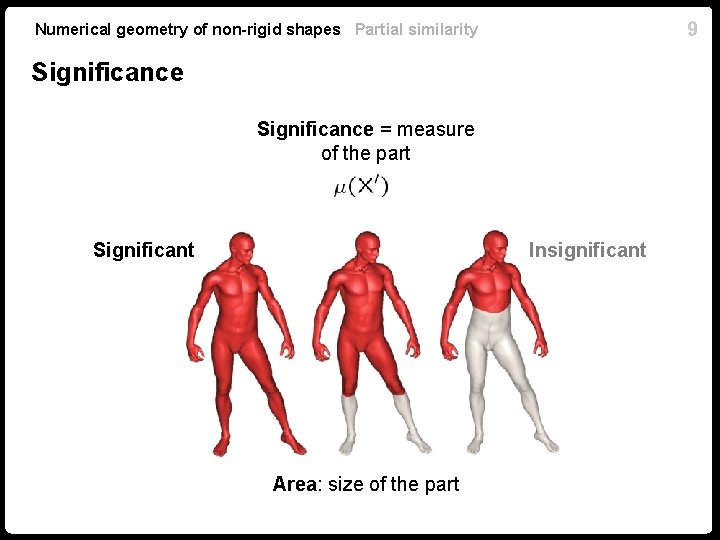
9 Numerical geometry of non-rigid shapes Partial similarity Significance = measure of the part Significant Insignificant Area: size of the part

Numerical geometry of non-rigid shapes Partial similarity Significance n Problem: how to select significant parts? n Significance of a part is a semantic definition n Different shapes may have different definition of significance 10

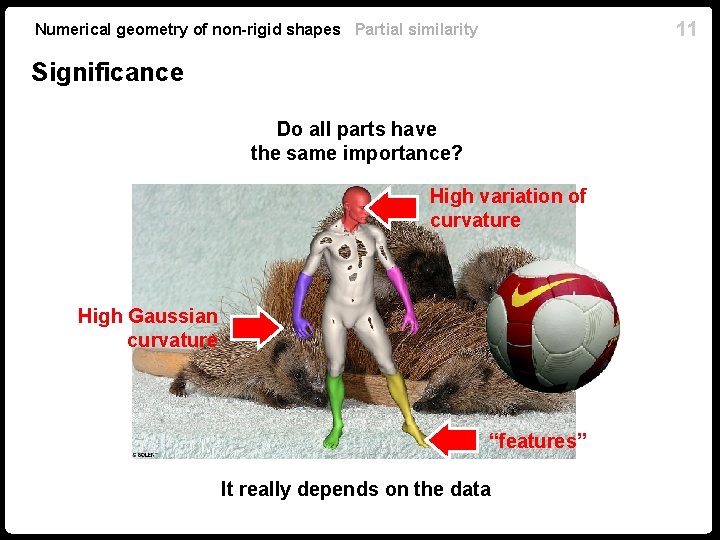
11 Numerical geometry of non-rigid shapes Partial similarity Significance Do all parts have the same importance? High variation of curvature High Gaussian curvature “features” It really depends on the data

12 Numerical geometry of non-rigid shapes Partial similarity Statistical significance Query q syzygy in astronomy means alignment of three bodies of the solar system along a straight or nearly straight line. a planet is in Significance of a term t syzygy with the earth and sun when it is in opposition or conjunction. the moon is in syzygy with the earth and sun when it is new or full. Frequent = important Term frequency A. Bronstein, M. Bronstein, Y. Carmon, R. Kimmel, CVA 2009 Database D or the syzygy in is Rare = discriminative Frequent = nondiscriminative Inverse document frequency

Numerical geometry of non-rigid shapes Partial similarity Numerical example A. Bronstein, M. Bronstein, Y. Carmon, R. Kimmel, CVA 2009 13

Numerical geometry of non-rigid shapes Partial similarity Multicriterion optimization n Simultaneously minimize dissimilarity and insignificance over all the possible pairs of parts n This type of problems is called multicriterion optimization n Vector objective function n How to solve a multicriterion optimization problem? 14

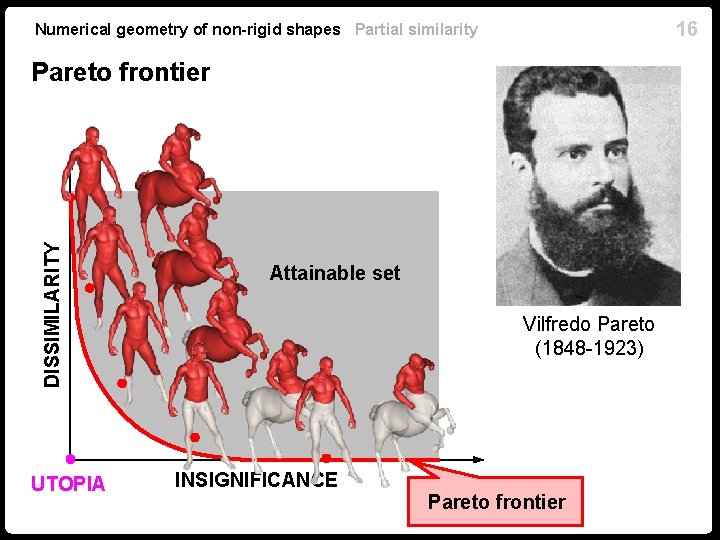
15 Numerical geometry of non-rigid shapes Partial similarity Pareto optimality A solution is said to be a global optimum of an optimization problem A solution is said to be a Pareto optimum of a multicriterion optimization problem if there is no other such that Traditional optimization if there is no other such that Multicriterion optimization n Optimum is a solution such that there is no other better solution n In multicriterion case, better = all the criteria are better

16 Numerical geometry of non-rigid shapes Partial similarity DISSIMILARITY Pareto frontier UTOPIA Attainable set Vilfredo Pareto (1848 -1923) INSIGNIFICANCE Pareto frontier

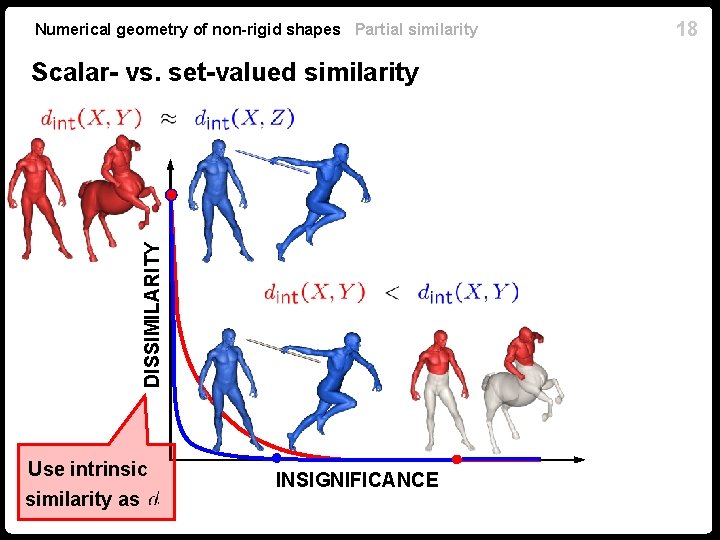
Numerical geometry of non-rigid shapes Partial similarity Set-valued partial similarity n The entire Pareto frontier is a set-valued distance n The dissimilarity at coincides with full similarity 17

Numerical geometry of non-rigid shapes Partial similarity DISSIMILARITY Scalar- vs. set-valued similarity Use intrinsic similarity as INSIGNIFICANCE 18

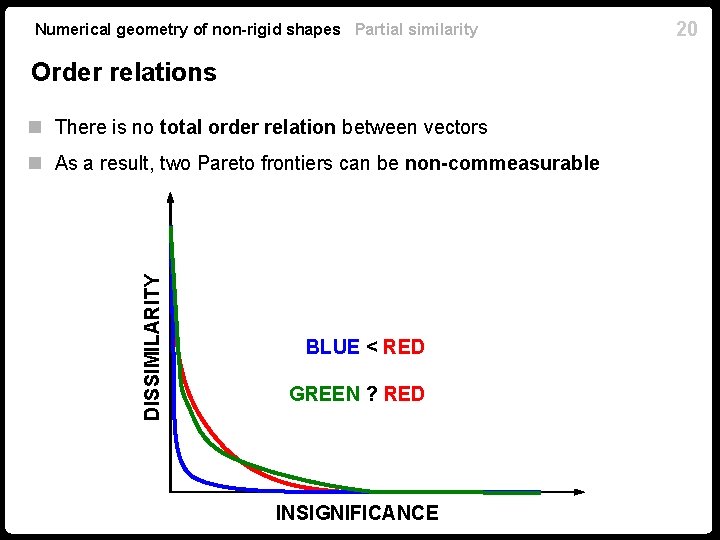
19 Numerical geometry of non-rigid shapes Partial similarity Order relations What is better: (1, 1) or (0. 5, 0. 5)? What is better: (1, 0. 5) or (0. 5, 1)? Is a crocodile green or ?

Numerical geometry of non-rigid shapes Partial similarity Order relations n There is no total order relation between vectors DISSIMILARITY n As a result, two Pareto frontiers can be non-commeasurable BLUE < RED GREEN ? RED INSIGNIFICANCE 20

21 Numerical geometry of non-rigid shapes Partial similarity Scalar-valued partial similarity In order to compare set-valued partial similarities, they should be scalarized Define scalar-valued partial similarity Can be written as using Lagrange multiplier DISSIMILARITY n Fix a value of insignificance INSIGNIFICANCE

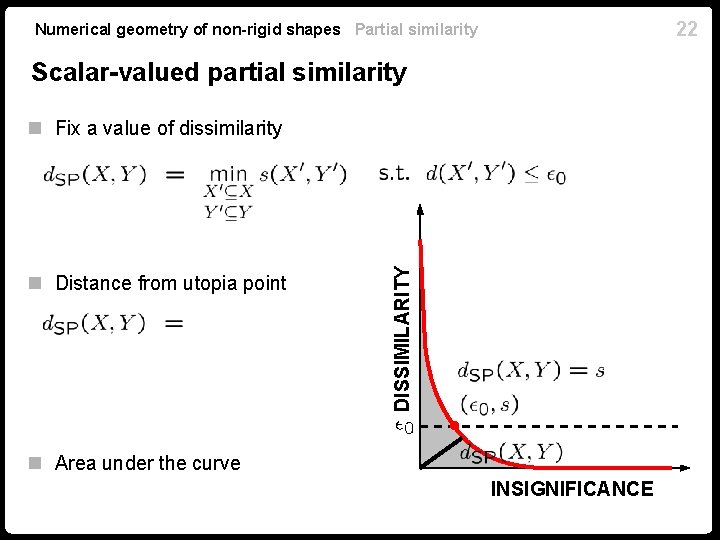
22 Numerical geometry of non-rigid shapes Partial similarity Scalar-valued partial similarity n Distance from utopia point DISSIMILARITY n Fix a value of dissimilarity n Area under the curve INSIGNIFICANCE

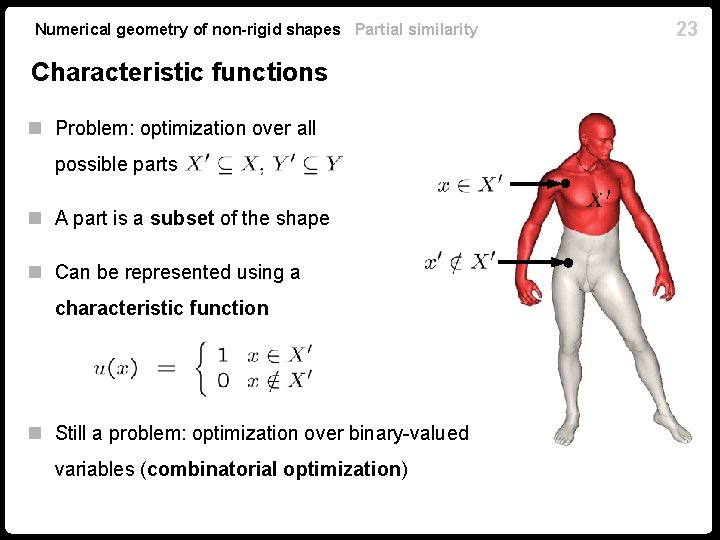
Numerical geometry of non-rigid shapes Partial similarity Characteristic functions n Problem: optimization over all possible parts n A part is a subset of the shape n Can be represented using a characteristic function n Still a problem: optimization over binary-valued variables (combinatorial optimization) 23

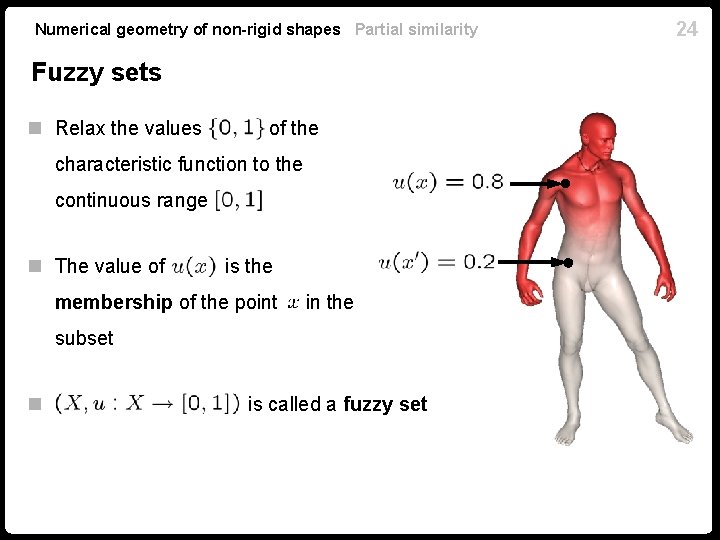
Numerical geometry of non-rigid shapes Partial similarity Fuzzy sets n Relax the values of the characteristic function to the continuous range n The value of is the membership of the point in the subset n is called a fuzzy set 24

Numerical geometry of non-rigid shapes Partial similarity Fuzzy partial similarity Compute partial similarity using fuzzy parts n Fuzzy insignificance n Fuzzy dissimilarity where is the weighted distortion 25

Numerical geometry of non-rigid shapes Partial similarity Numerical optimization GMDS problem: A. Bronstein, M. Bronstein, A. Bruckstein, R. Kimmel, IJCV 2008; A. Bronstein, M. Bronstein, NORDIA 2008 26

Numerical geometry of non-rigid shapes Partial similarity Numerical optimization 1 2 Freeze parts and solve for correspondence Freeze correspondence and solve for parts A. Bronstein, M. Bronstein, A. Bruckstein, R. Kimmel, IJCV 2008; A. Bronstein, M. Bronstein, NORDIA 2008 27

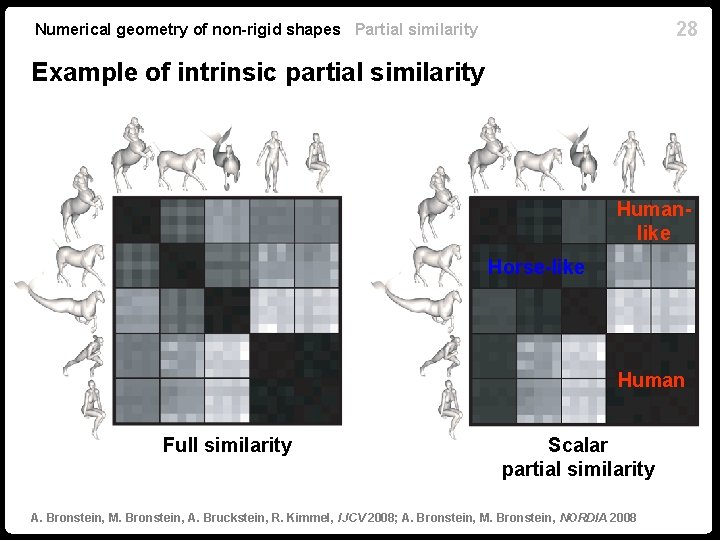
28 Numerical geometry of non-rigid shapes Partial similarity Example of intrinsic partial similarity Humanlike Horse-like Human Full similarity Scalar partial similarity Partial similarity A. Bronstein, M. Bronstein, A. Bruckstein, R. Kimmel, IJCV 2008; A. Bronstein, M. Bronstein, NORDIA 2008

Numerical geometry of non-rigid shapes Partial similarity 29 Extrinsic partial similarity How to make ICP compare partially similar shapes? Introduce weights into the shape-to-shape distance to reject points with bad correspondence Possible selection of weights: where is a threshold on normals is a threshold on distance and are the normals to shapes and

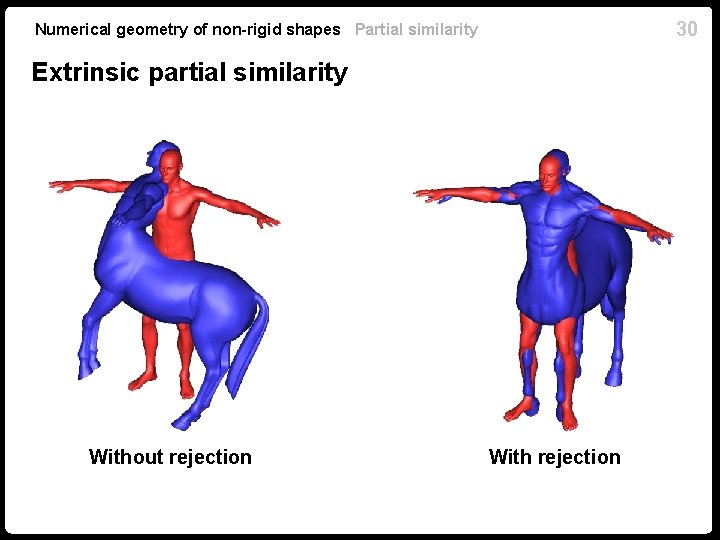
30 Numerical geometry of non-rigid shapes Partial similarity Extrinsic partial similarity Without rejection With rejection

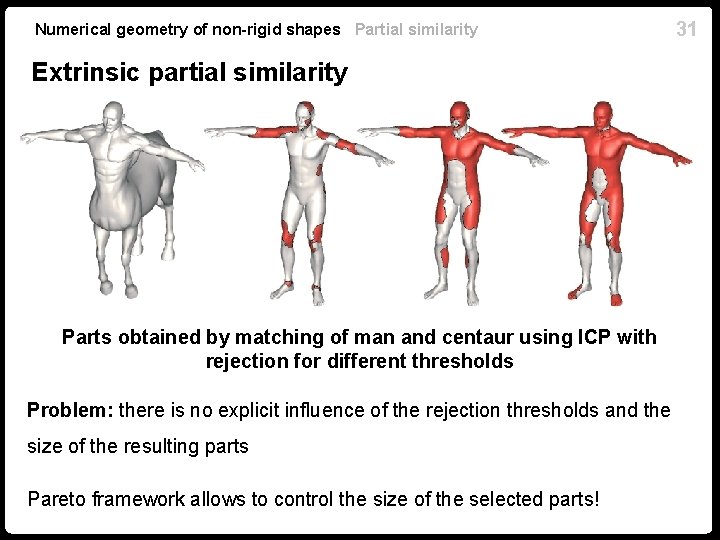
Numerical geometry of non-rigid shapes Partial similarity Extrinsic partial similarity Parts obtained by matching of man and centaur using ICP with rejection for different thresholds Problem: there is no explicit influence of the rejection thresholds and the size of the resulting parts Pareto framework allows to control the size of the selected parts! 31

Numerical geometry of non-rigid shapes Partial similarity Extrinsic partial similarity Correspondence stage (fixed n Closest point correspondence n Weighted rigid alignment n Correspondence and ) 32

Numerical geometry of non-rigid shapes Partial similarity Extrinsic partial similarity Part selection stage (fixed and ) 33

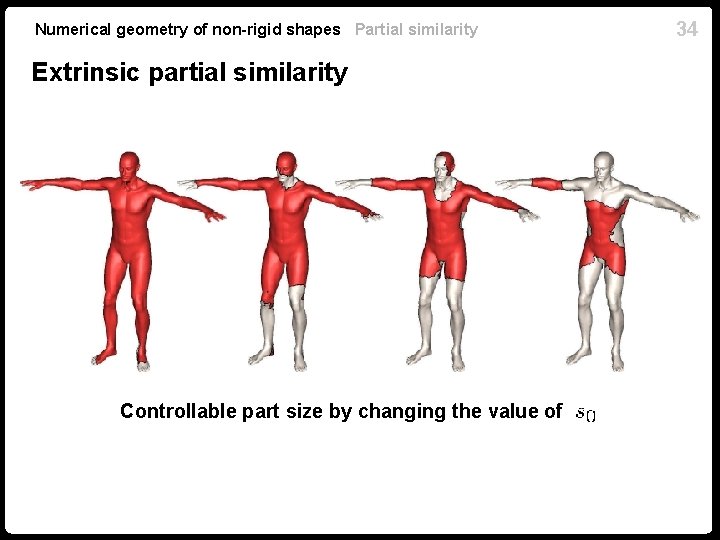
Numerical geometry of non-rigid shapes Partial similarity Extrinsic partial similarity Controllable part size by changing the value of 34

Numerical geometry of non-rigid shapes Partial similarity Not only size matters What is better? . . . …or one large part? Many small parts… A. Bronstein, M. Bronstein, A. Bruckstein, R. Kimmel, IJCV 2008; A. Bronstein, M. Bronstein, NORDIA 2008 35

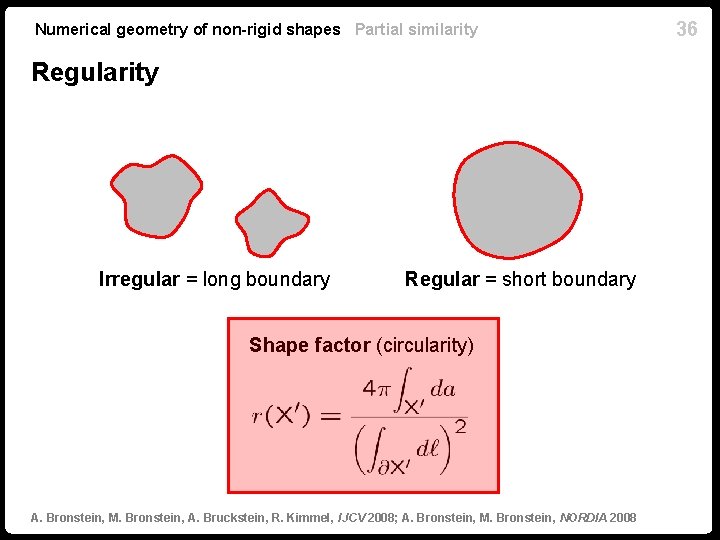
Numerical geometry of non-rigid shapes Partial similarity Regularity Irregular = long boundary Regular = short boundary Shape factor (circularity) A. Bronstein, M. Bronstein, A. Bruckstein, R. Kimmel, IJCV 2008; A. Bronstein, M. Bronstein, NORDIA 2008 36

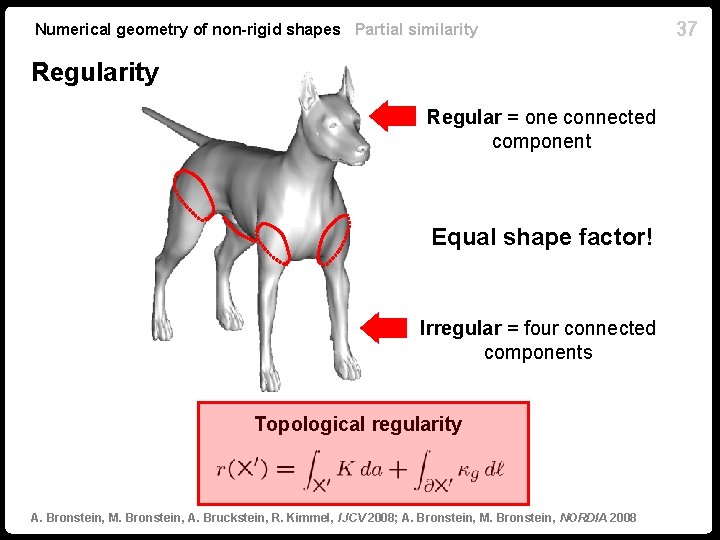
Numerical geometry of non-rigid shapes Partial similarity Regular = one connected component Equal shape factor! Irregular = four connected components Topological regularity A. Bronstein, M. Bronstein, A. Bruckstein, R. Kimmel, IJCV 2008; A. Bronstein, M. Bronstein, NORDIA 2008 37

Numerical geometry of non-rigid shapes Partial similarity Mumford-Shah functional Salvation comes from image segmentation [Mumford&Shah]: given image replace by a membership function The two problems are equivalent , find the segmented region 38

Numerical geometry of non-rigid shapes Partial similarity Mumford-Shah functional In our problem, we need only the integral along the boundary which becomes in the fuzzy setting 39

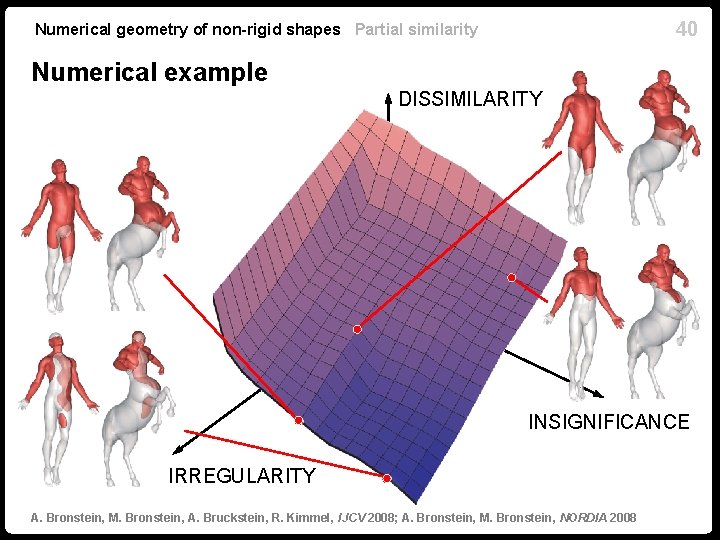
40 Numerical geometry of non-rigid shapes Partial similarity Numerical example DISSIMILARITY INSIGNIFICANCE IRREGULARITY A. Bronstein, M. Bronstein, A. Bruckstein, R. Kimmel, IJCV 2008; A. Bronstein, M. Bronstein, NORDIA 2008

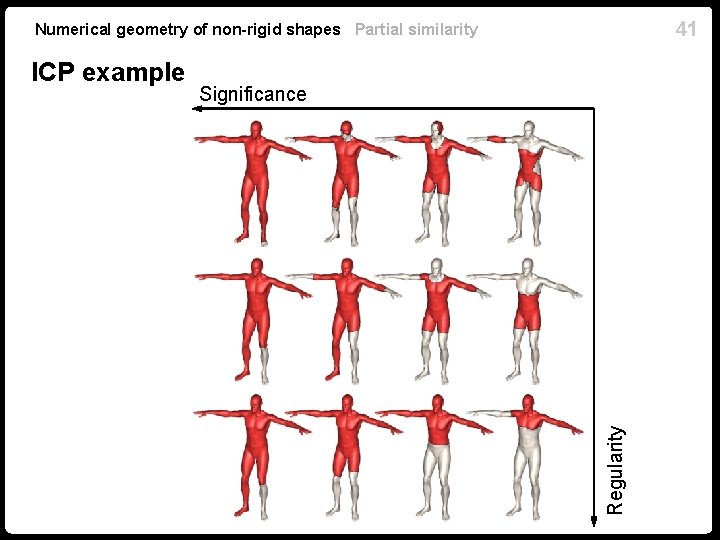
41 Numerical geometry of non-rigid shapes Partial similarity Significance Regularity ICP example