Numerical geometry of nonrigid shapes Multidimensional scaling 1

Numerical geometry of non-rigid shapes Multidimensional scaling 1 Multidimensional scaling Lecture 5 © Alexander & Michael Bronstein tosca. cs. technion. ac. il/book Numerical geometry of non-rigid shapes Stanford University, Winter 2009

Numerical geometry of non-rigid shapes Multidimensional scaling Cinderella 2. 0 2

Numerical geometry of non-rigid shapes Multidimensional scaling If it doesn’t fit, you must acquit! A glove allegedly dropped by Simpson at the crime scene A pivotal point of the trial: O. J. Simpson is unable to put on the glove 3

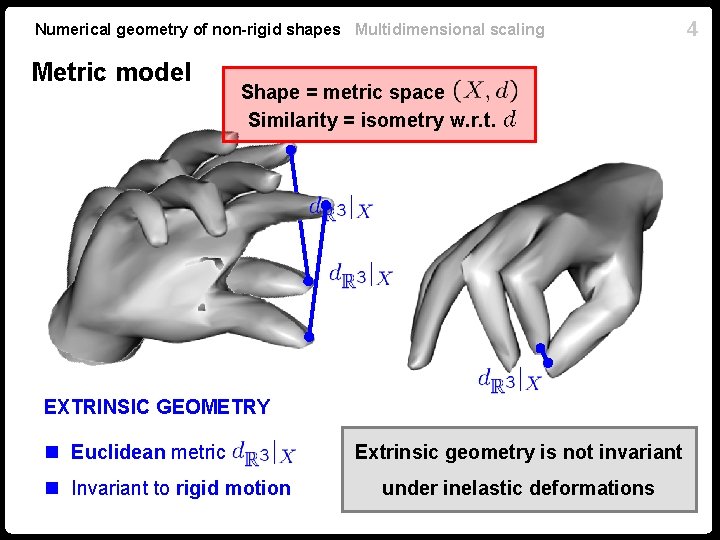
Numerical geometry of non-rigid shapes Multidimensional scaling Metric model Shape = metric space Similarity = isometry w. r. t. EXTRINSIC GEOMETRY n Euclidean metric n Invariant to rigid motion Extrinsic geometry is not invariant under inelastic deformations 4

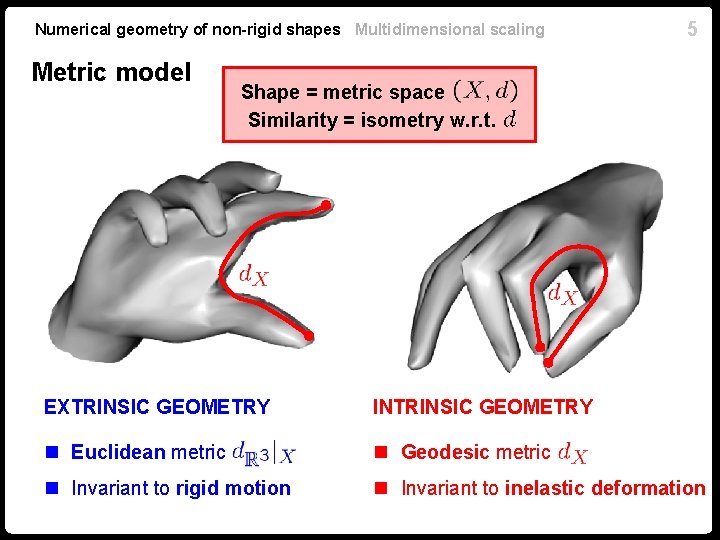
Numerical geometry of non-rigid shapes Multidimensional scaling Metric model 5 Shape = metric space Similarity = isometry w. r. t. EXTRINSIC GEOMETRY INTRINSIC GEOMETRY n Euclidean metric n Geodesic metric n Invariant to rigid motion n Invariant to inelastic deformation

Numerical geometry of non-rigid shapes Multidimensional scaling Intrinsic vs. extrinsic similarity EXTRINSIC SIMILARITY INTRINSIC SIMILARITY Part of the same metric space Two different metric spaces SOLUTION: Find a representation of in a common metric space and 6

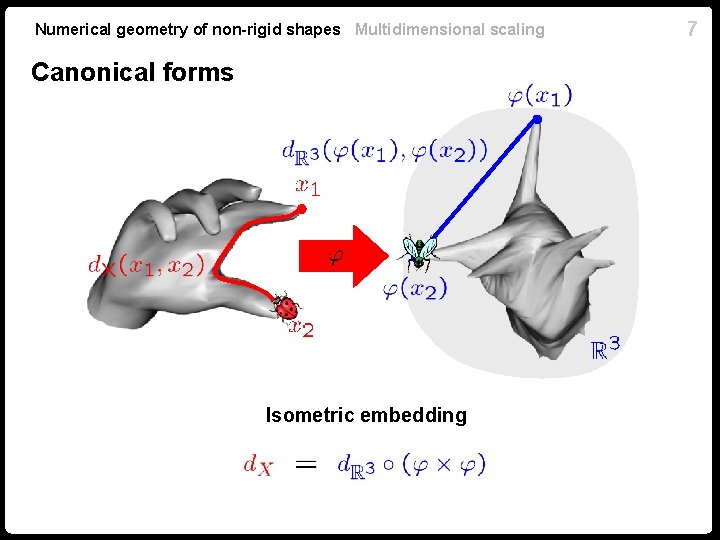
Numerical geometry of non-rigid shapes Multidimensional scaling Canonical forms Isometric embedding 7

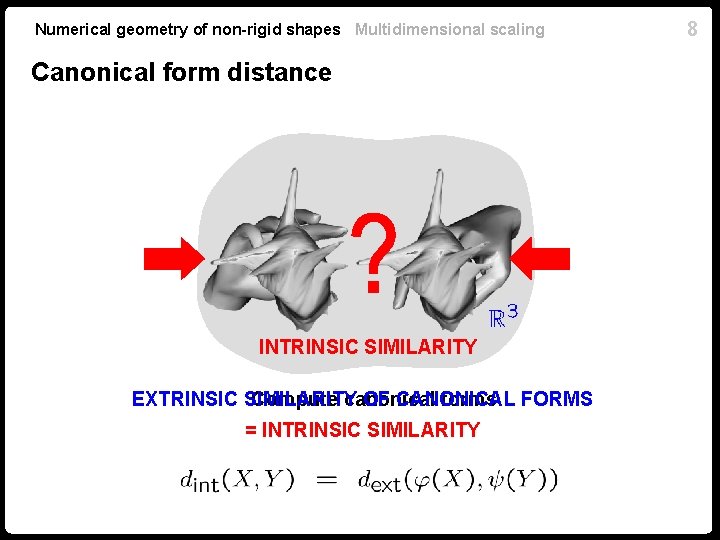
Numerical geometry of non-rigid shapes Multidimensional scaling Canonical form distance INTRINSIC SIMILARITY Compute canonical forms FORMS EXTRINSIC SIMILARITY OF CANONICAL = INTRINSIC SIMILARITY 8

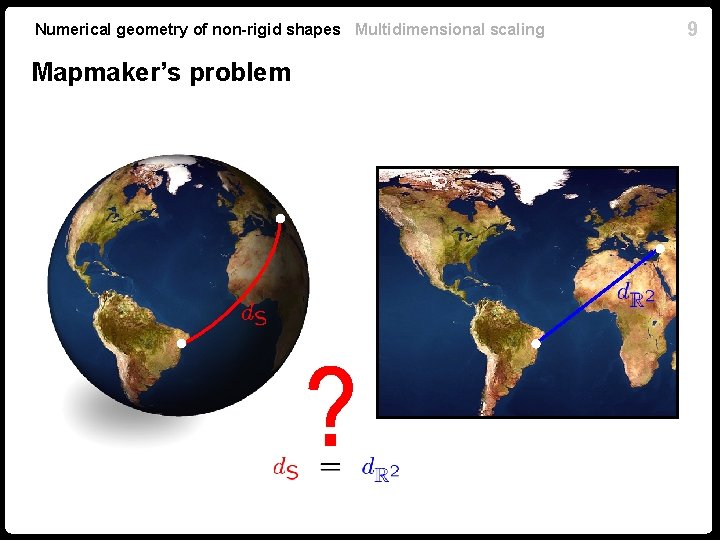
Numerical geometry of non-rigid shapes Multidimensional scaling Mapmaker’s problem 9

Numerical geometry of non-rigid shapes Multidimensional scaling 10 Mapmaker’s problem A sphere has non-zero curvature, therefore, it is not isometric to the plane (a consequence of Theorema egregium) Karl Friedrich Gauss (1777 -1855)

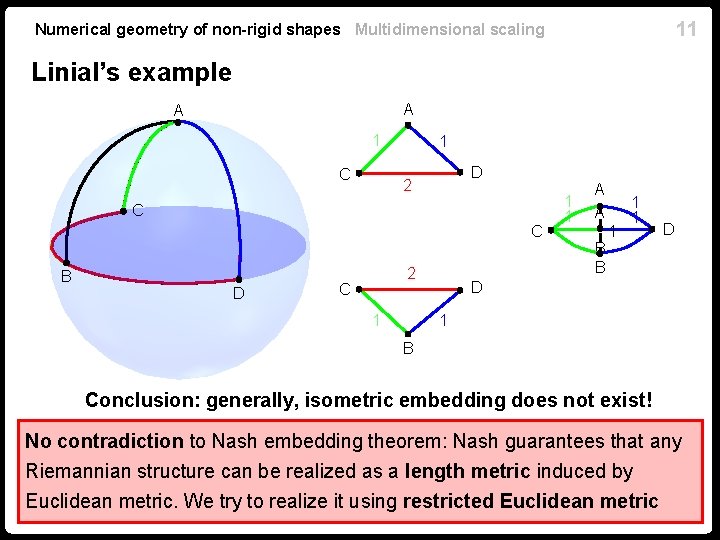
11 Numerical geometry of non-rigid shapes Multidimensional scaling Linial’s example A A 1 C 1 D 2 C C B D 2 C 1 1 1 A A B B 1 1 1 D D 1 B Conclusion: generally, isometric embedding does not exist! No contradiction to Nash embedding theorem: Nash guarantees that any Riemannian structure can be realized as a length metric induced by Euclidean metric. We try to realize it using restricted Euclidean metric

Numerical geometry of non-rigid shapes Multidimensional scaling Minimum distortion embedding 12

Numerical geometry of non-rigid shapes Multidimensional scaling Find an embedding into that distorts the distances the least by solving the optimization problem where n The function are the coordinates of the canonical form measuring the distortion of distances is called stress n The problem is called multidimensional scaling (MDS) 13

Numerical geometry of non-rigid shapes Multidimensional scaling 14 Stress The stress is a function of the canonical form coordinates the distances n L 2 -stress n Lp-stress n L -stress (distortion) and

Numerical geometry of non-rigid shapes Multidimensional scaling Matrix expression of L 2 -stress Some notation: n - an matrix of canonical form coordinates (each row corresponds to a point) n Shorthand notation for Euclidean distances Write the stress as 1 2 15

Numerical geometry of non-rigid shapes Multidimensional scaling Term 1 16

Numerical geometry of non-rigid shapes Multidimensional scaling Term 1 Matrices commute under trace operator where is and matrix with elements 17

Numerical geometry of non-rigid shapes Multidimensional scaling Term 2 For and zero otherwise 18

Numerical geometry of non-rigid shapes Multidimensional scaling Term 2 where is and matrix-valued function with elements 19

Numerical geometry of non-rigid shapes Multidimensional scaling LS-MDS Minimization of L 2 -stress is called least squares MDS (LS-MDS) n variables n Non-linear n Non-convex (this liable to local convergence) n Optimum defined up to Euclidean transformation 20

21 Numerical geometry of non-rigid shapes Multidimensional scaling Gradient of L 2 -stress Quadratic in Recall exercise in optimization Nonlinear in Constant in

Numerical geometry of non-rigid shapes Multidimensional scaling Complexity n Stress computation complexity: n Stress gradient computation complexity: n Steepest descent with line search may be prohibitively expensive (requires multiple evaluations of the stress and the gradient) 22

Numerical geometry of non-rigid shapes Multidimensional scaling Observation By Cauchy-Schwarz inequality for all and Equality is achieved for Write it differently: 23

Numerical geometry of non-rigid shapes Multidimensional scaling Observation Consider the nonlinear term in the stress 24

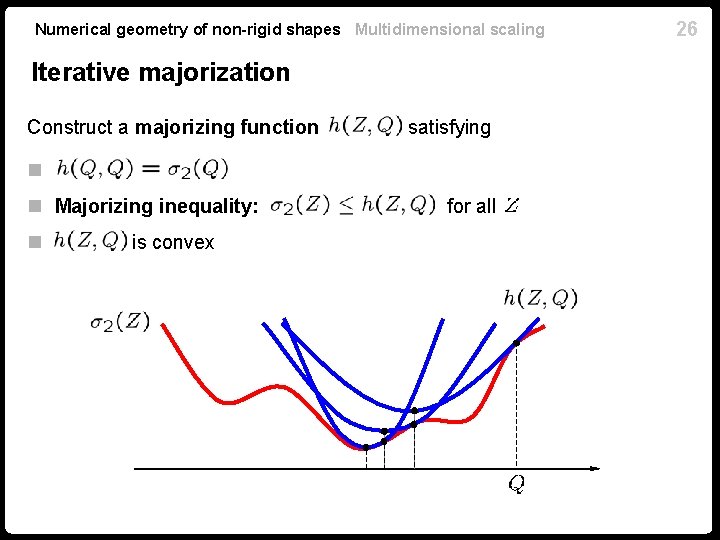
Numerical geometry of non-rigid shapes Multidimensional scaling Majorizing inequality Equality is achieved for [de Leeuw, 1977] We have a quadratic majorizing function to use in iterative majorization algorithm! Jan de Leeuw 25

Numerical geometry of non-rigid shapes Multidimensional scaling Iterative majorization Construct a majorizing function satisfying n. n Majorizing inequality: n is convex for all 26

Numerical geometry of non-rigid shapes Multidimensional scaling 27 Iterative majorization n Start with some n Find such that n Update iterate n Increment iteration counter n Solution Until convergence

Numerical geometry of non-rigid shapes Multidimensional scaling 28 Iterative majorization The majorizing function is quadratic! Analytic expression for the minimim Analytic expression for pseudoinverse:

29 Numerical geometry of non-rigid shapes Multidimensional scaling SMACOF algorithm n Start with some n Update iterate n Increment iteration counter Until convergence n Solution The algorithm is called SMACOF (Scaling by Minimizing A COnvex Function)

Numerical geometry of non-rigid shapes Multidimensional scaling 30 SMACOF algorithm vs steepest descent SMACOF is a constant-step gradient descent! n Majorization guarantees monotonically decreasing sequence of stress values (untypical behavior for constant-step steepest descent) n No guarantee of global convergence n Iteration cost:

Numerical geometry of non-rigid shapes Multidimensional scaling ® MATLAB intermezzo SMACOF algorithm Canonical forms 31

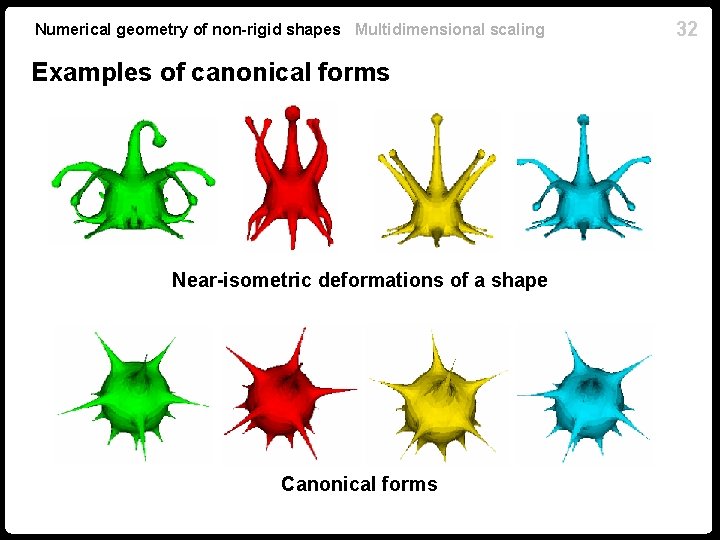
Numerical geometry of non-rigid shapes Multidimensional scaling Examples of canonical forms Near-isometric deformations of a shape Canonical forms 32

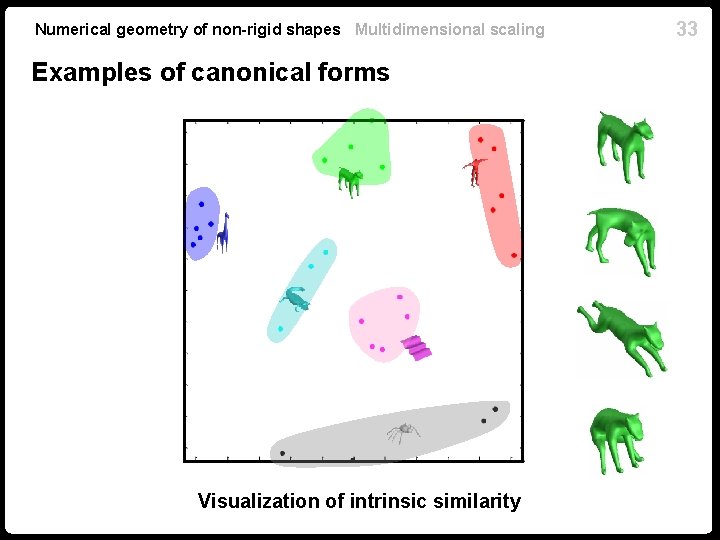
Numerical geometry of non-rigid shapes Multidimensional scaling Examples of canonical forms Visualization of intrinsic similarity 33

Numerical geometry of non-rigid shapes Multidimensional scaling Weighted stress where are some fixed weights Matrix expression where is and matrix with elements SMACOF algorithm can be used to minimize weighted stress! 34

35 Numerical geometry of non-rigid shapes Multidimensional scaling Variations on the stress theme Generic form of the stress where is some norm For example, gives the Lp-stress The necessary condition for to be the minimizer of is

Numerical geometry of non-rigid shapes Multidimensional scaling Variations on the stress theme Idea: minimize weighted stress instead of the generic stress and choose the weights such that the two are equivalent If the weights are selected as the minimizers of Since and will coincide is unknown in advance, iterate! 36

37 Numerical geometry of non-rigid shapes Multidimensional scaling Iteratively reweighted LS n Start with some and n Find using as an initialization n Update weights Until convergence n Increment iteration counter The algorithm is called Iteratively Reweighted Least Squares (IRLS)

Numerical geometry of non-rigid shapes Multidimensional scaling L -stress Optimization problem can be written equivalently as a constrained problem is called an artificial variable 38

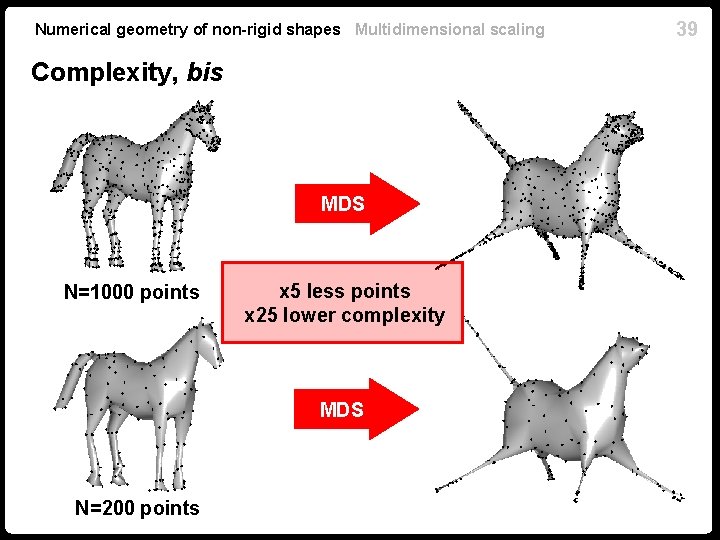
Numerical geometry of non-rigid shapes Multidimensional scaling Complexity, bis MDS N=1000 points x 5 less points x 25 lower complexity MDS N=200 points 39

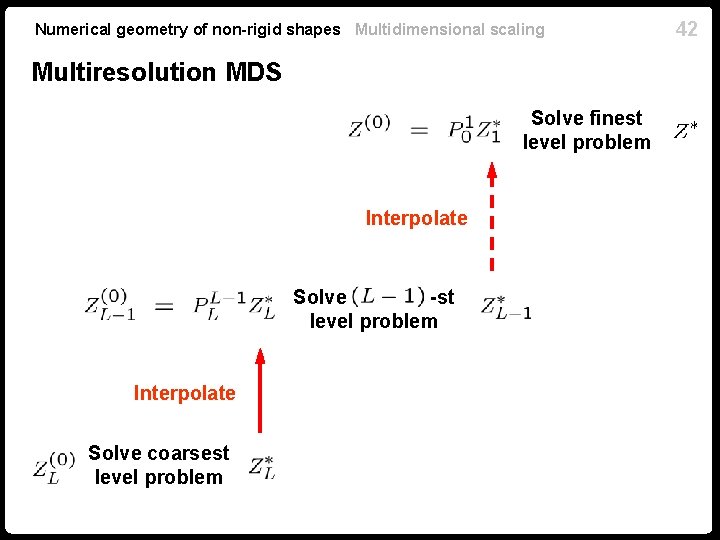
Numerical geometry of non-rigid shapes Multidimensional scaling 40 Multiresolution MDS n Bottom-up approach: solve coarse level MDS problem to initialize fine level problem n Reduce complexity (less fine-level iterations) n Reduce the risk of local convergence (good initialization) n Can be performed on multiple resolution levels

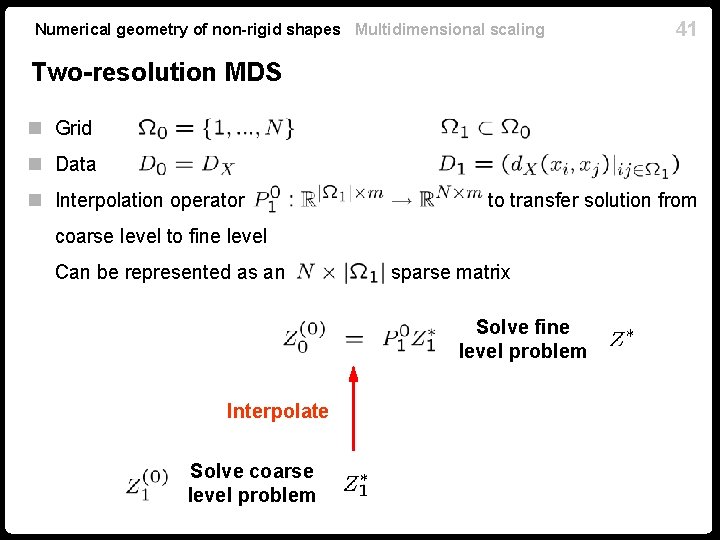
Numerical geometry of non-rigid shapes Multidimensional scaling 41 Two-resolution MDS n Grid n Data n Interpolation operator to transfer solution from coarse level to fine level Can be represented as an sparse matrix Solve fine level problem Interpolate Solve coarse level problem

Numerical geometry of non-rigid shapes Multidimensional scaling Multiresolution MDS Solve finest level problem Interpolate Solve -st level problem Interpolate Solve coarsest level problem 42

43 Numerical geometry of non-rigid shapes Multidimensional scaling Multiresolution MDS algorithm n Hierarchy of grids n Hierarchy of data n Interpolation operators n Start with coarsest-level initialization n Solve the l-th level MDS problem For using as initialization n Interpolate to next level n Solve finest level problem using as initialization

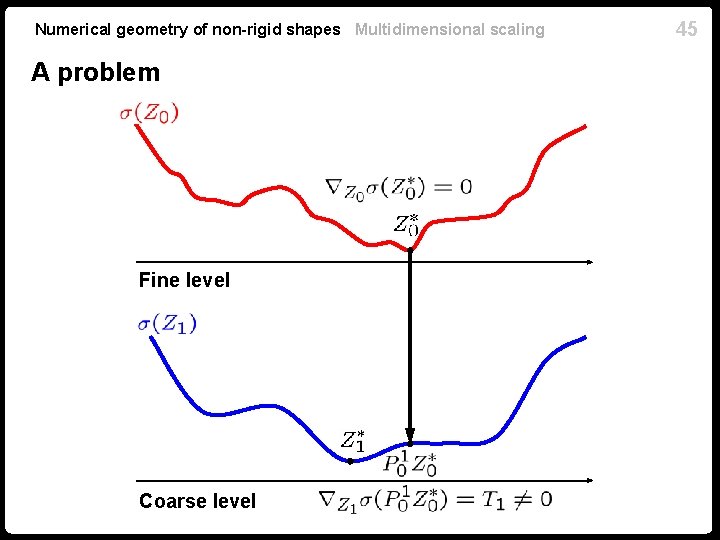
44 Numerical geometry of non-rigid shapes Multidimensional scaling Top-down approach n Start with a fine-level initialization n Decimate fine-level initialization to the coarse grid Typically n Solve the coarse-level MDS problem using as initialization n Improve the fine-level solution propagating the coarse-level error

Numerical geometry of non-rigid shapes Multidimensional scaling A problem Fine level Coarse level 45

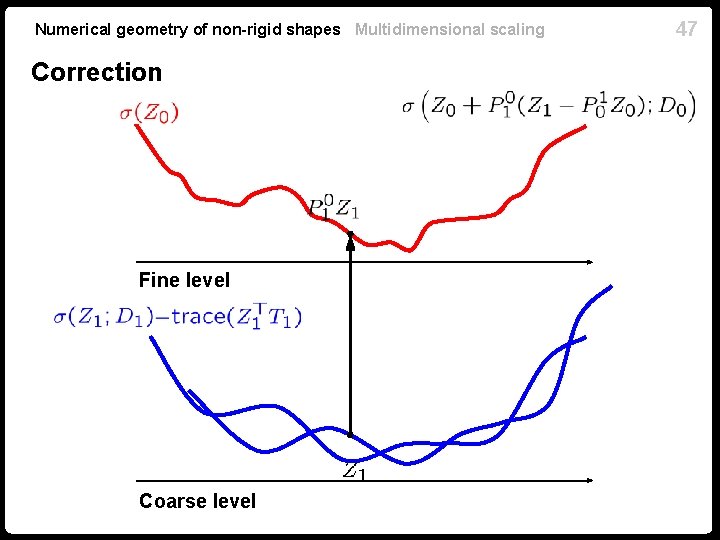
Numerical geometry of non-rigid shapes Multidimensional scaling 46 Correction The fine- and the coarse-level minimizers do not coincide! is called a residual Force consistency of the coarse- and fine-level problems by introducing a correction term into the stress which gives the gradient

Numerical geometry of non-rigid shapes Multidimensional scaling Correction Fine level Coarse level 47

Numerical geometry of non-rigid shapes Multidimensional scaling Correction In order to guarantee consistency, must satisfy at Chain rule which gives the correction term Verify: is the minimizer of coarse-level problem with correction, 48

Numerical geometry of non-rigid shapes Multidimensional scaling Modified stress Another problem: the coarse grid problem is unbounded for Can grow arbitrarily Fix the translation ambiguity by adding a quadratic penalty to the stress is called the modified stress [Bronstein et al. , 05] The modified coarse grid problem is bounded 49

Numerical geometry of non-rigid shapes Multidimensional scaling Two-grid MDS n Iteratively improve the fine-level solution using coarse grid residual n External iteration is called cycle Correct fine level solution Decimate Solve corrected coarse level problem Interpolate 50

Numerical geometry of non-rigid shapes Multidimensional scaling Two-grid MDS n Perform a few optimization iterations at fine level between cycles (relaxation) Correct fine level solution Relax Decimate Solve corrected coarse level problem Interpolate 51

Numerical geometry of non-rigid shapes Multidimensional scaling 52 Two-grid MDS algorithm n Start with fine-level initialization n Produce an improved fine-level solution making a few iterations on by initialized with n Decimate fine-level solution n Correction: n Solve the coarse-level corrected MDS problem using as initialization n Transfer residual: n Update iterate n Solution Until convergence

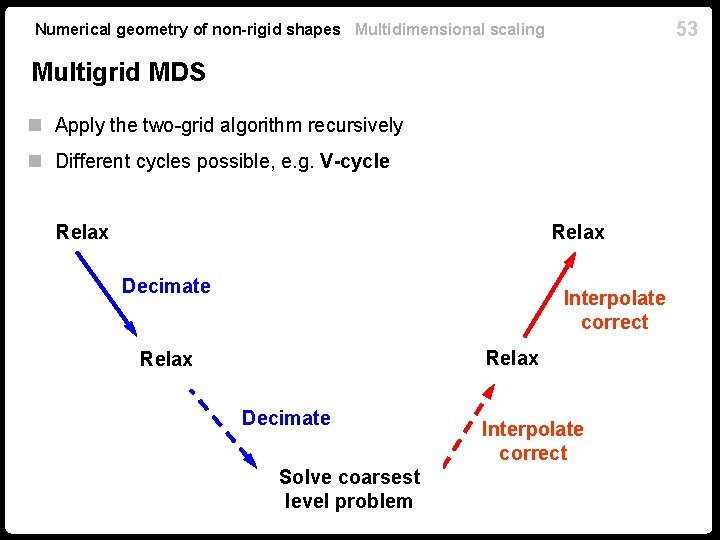
53 Numerical geometry of non-rigid shapes Multidimensional scaling Multigrid MDS n Apply the two-grid algorithm recursively n Different cycles possible, e. g. V-cycle Relax Decimate Interpolate correct Relax Decimate Solve coarsest level problem Interpolate correct

Numerical geometry of non-rigid shapes Multidimensional scaling ® MATLAB intermezzo Multigrid MDS 54

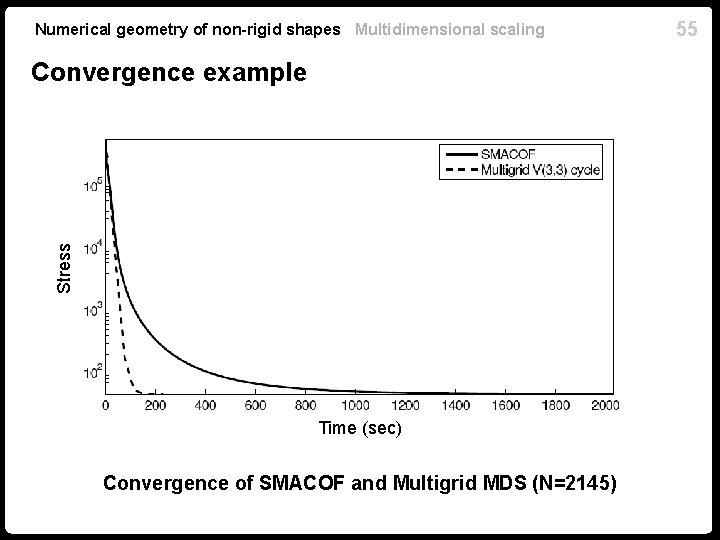
Numerical geometry of non-rigid shapes Multidimensional scaling Stress Convergence example Time (sec) Convergence of SMACOF and Multigrid MDS (N=2145) 55

Numerical geometry of non-rigid shapes Multidimensional scaling How to accelerate convergence? Let be a sequence of iterates produced by some optimization algorithms converging to Denote by Construct a new sequence in the sense the remained converging faster to 56

Numerical geometry of non-rigid shapes Multidimensional scaling Vector extrapolation Construct the new sequence as a transformation of iterates Particular choice: linear combination Question: how to choose the coefficients Ideally, hence ? 57

Numerical geometry of non-rigid shapes Multidimensional scaling 58 Reduced rank extrapolation (RRE) Problem: depends on unknown Eliminate this dependence by considering the difference which ideally should vanish. Result: solve the constrained linear system of equations in Typically variables hence the system is over-determined and must be solved approximately using least-squares

Numerical geometry of non-rigid shapes Multidimensional scaling 59 Optimization with vector extrapolation n Start with some and n Generate iterates using optimization on n Extrapolate from n Update n Increment iteration counter initialized by Until convergence

60 Numerical geometry of non-rigid shapes Multidimensional scaling Safeguarded optimization with vector extrapolation n Start with some and n Generate iterates using optimization on n Extrapolate initialized by from n If n else n Increment iteration counter Until convergence