Numerical geometry of nonrigid shapes Discrete Geometry 1

Numerical geometry of non-rigid shapes Discrete Geometry 1 Discrete Geometry Tutorial 2 © Maks Ovsjanikov, Alex & Michael Bronstein tosca. cs. technion. ac. il/book Numerical geometry of non-rigid shapes Stanford University, Winter 2009

Numerical geometry of non-rigid shapes Discrete Geometry Neighborhood of point in Discrete equivalent of metric ball 2

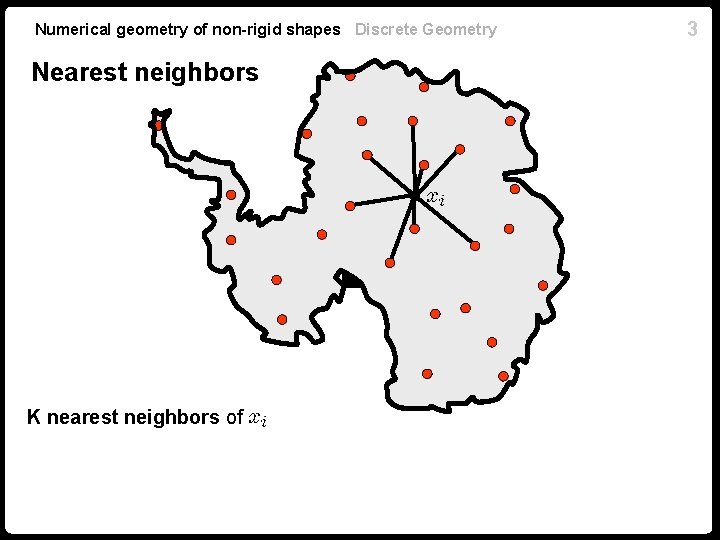
Numerical geometry of non-rigid shapes Discrete Geometry Nearest neighbors K nearest neighbors of 3

Numerical geometry of non-rigid shapes Discrete Geometry Connectivity n Neighborhood is a topological definition independent of a metric n Two points are adjacent (directly connected) if they belong to the same neighborhood n The connectivity structure can be represented as an undirected graph with vertices and Vertices Edges edges n Connectivity graph can be represented as a matrix 4

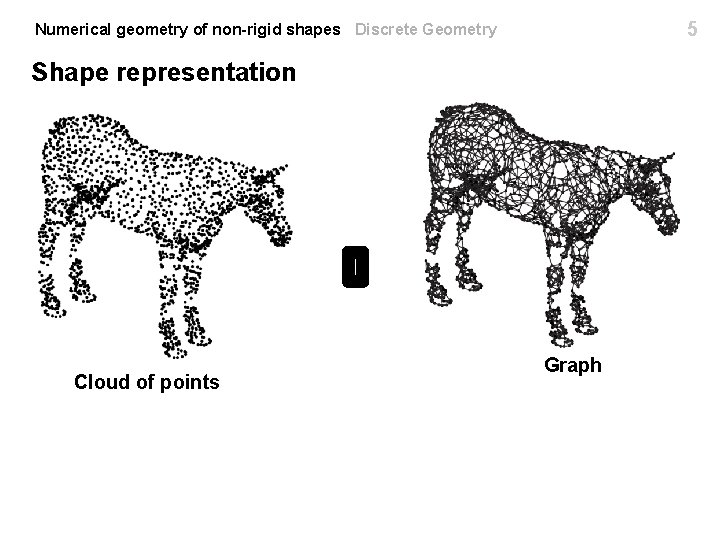
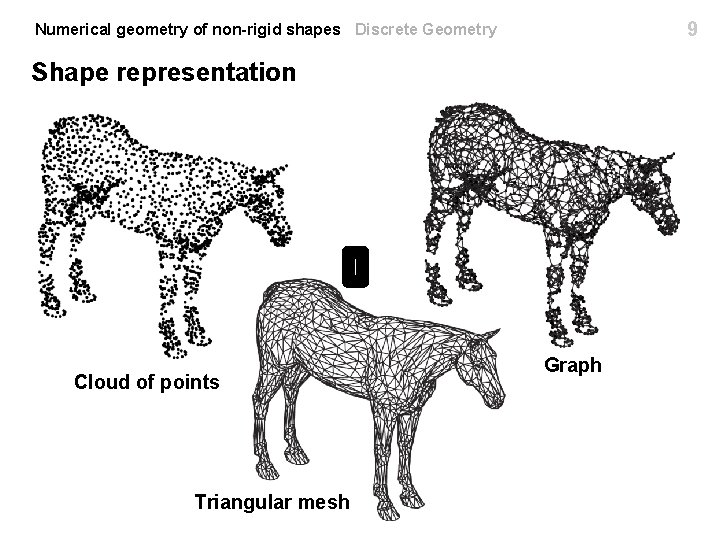
5 Numerical geometry of non-rigid shapes Discrete Geometry Shape representation Cloud of points Graph

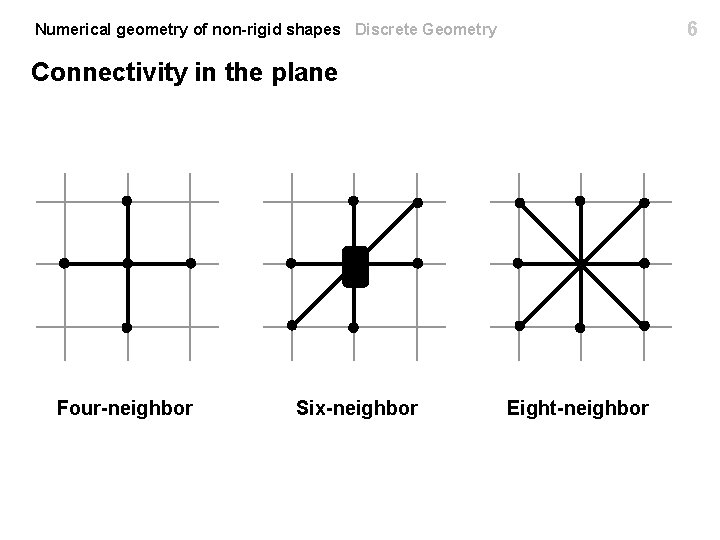
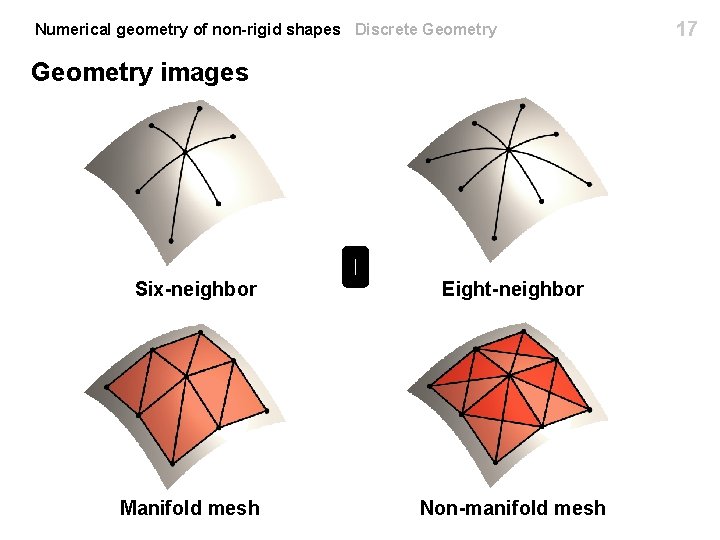
6 Numerical geometry of non-rigid shapes Discrete Geometry Connectivity in the plane Four-neighbor Six-neighbor Eight-neighbor

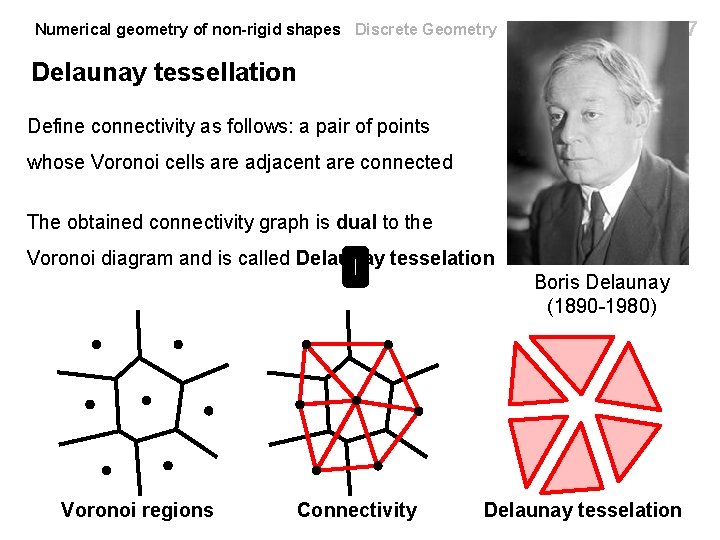
7 Numerical geometry of non-rigid shapes Discrete Geometry Delaunay tessellation Define connectivity as follows: a pair of points whose Voronoi cells are adjacent are connected The obtained connectivity graph is dual to the Voronoi diagram and is called Delaunay tesselation Boris Delaunay (1890 -1980) Voronoi regions Connectivity Delaunay tesselation

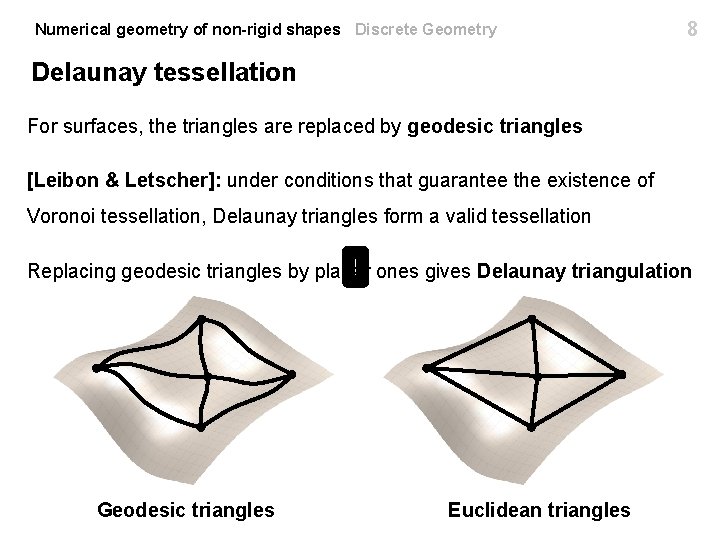
Numerical geometry of non-rigid shapes Discrete Geometry 8 Delaunay tessellation For surfaces, the triangles are replaced by geodesic triangles [Leibon & Letscher]: under conditions that guarantee the existence of Voronoi tessellation, Delaunay triangles form a valid tessellation Replacing geodesic triangles by planar ones gives Delaunay triangulation Geodesic triangles Euclidean triangles

9 Numerical geometry of non-rigid shapes Discrete Geometry Shape representation Cloud of points Triangular mesh Graph

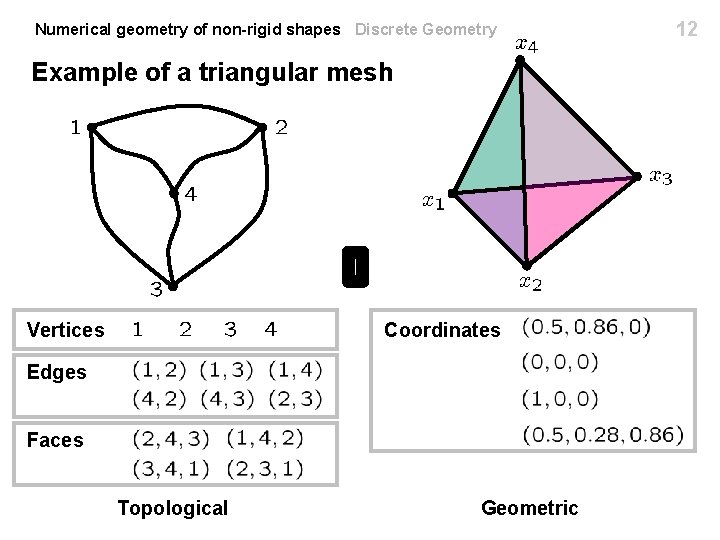
10 Numerical geometry of non-rigid shapes Discrete Geometry Triangular meshes A structure of the form consisting of n Vertices n Edges n Faces is called a triangular mesh The mesh is a purely topological object and does not contain any geometric properties The faces can be represented as an row is a vector of the form matrix of indices, where each , and

Numerical geometry of non-rigid shapes Discrete Geometry Triangular meshes The geometric realization of the mesh is defined by specifying the coordinates of the vertices for all The coordinates can be represented as an matrix The mesh is a piece-wise planar approximation obtained by gluing the triangular faces together, Triangular face 11

Numerical geometry of non-rigid shapes Discrete Geometry Example of a triangular mesh Vertices Coordinates Edges Faces Topological Geometric 12

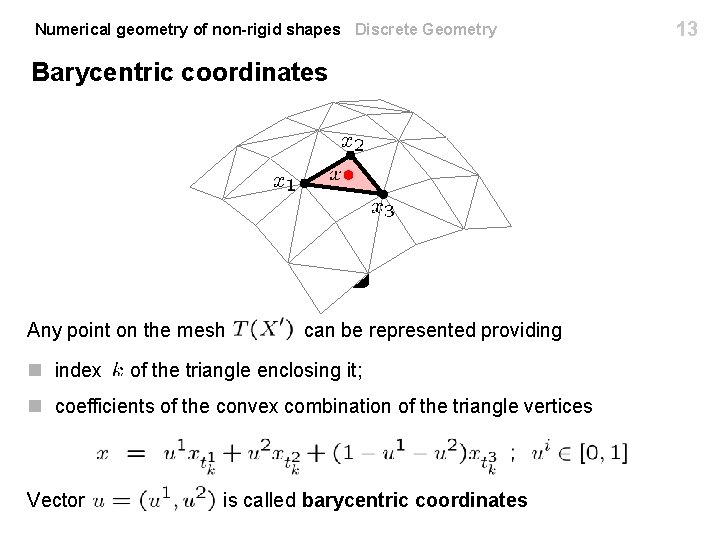
Numerical geometry of non-rigid shapes Discrete Geometry Barycentric coordinates Any point on the mesh n index can be represented providing of the triangle enclosing it; n coefficients of the convex combination of the triangle vertices Vector is called barycentric coordinates 13

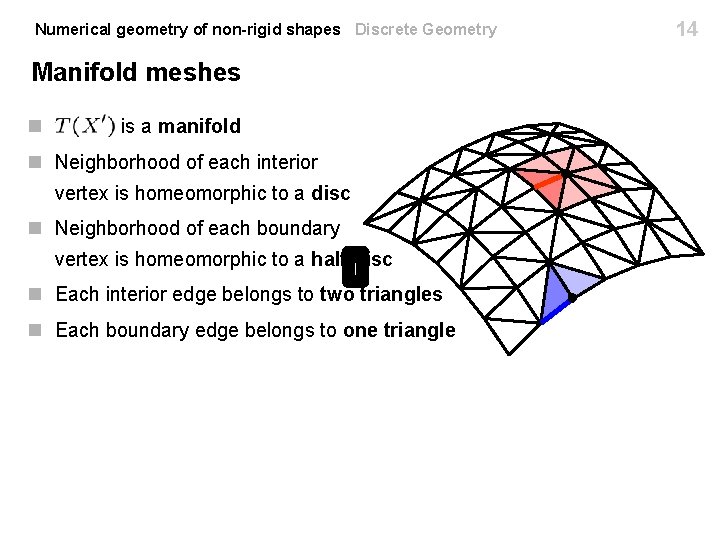
Numerical geometry of non-rigid shapes Discrete Geometry Manifold meshes n is a manifold n Neighborhood of each interior vertex is homeomorphic to a disc n Neighborhood of each boundary vertex is homeomorphic to a half-disc n Each interior edge belongs to two triangles n Each boundary edge belongs to one triangle 14

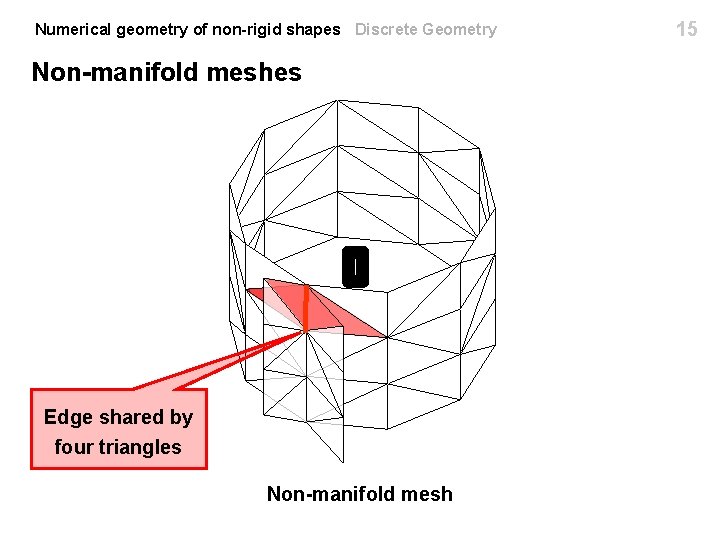
Numerical geometry of non-rigid shapes Discrete Geometry Non-manifold meshes Edge shared by four triangles Non-manifold mesh 15

Numerical geometry of non-rigid shapes Discrete Geometry images Surface Geometry image Global parametrization Sampling of parametrization domain on a Cartesian grid 16

Numerical geometry of non-rigid shapes Discrete Geometry images Six-neighbor Eight-neighbor Manifold mesh Non-manifold mesh 17

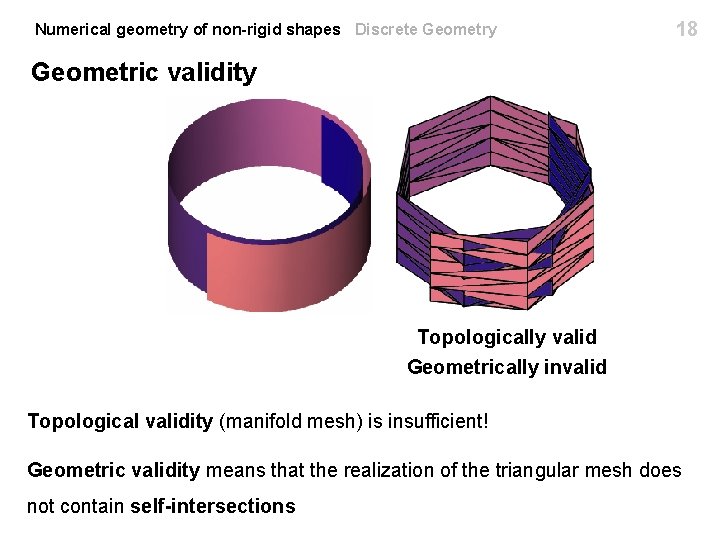
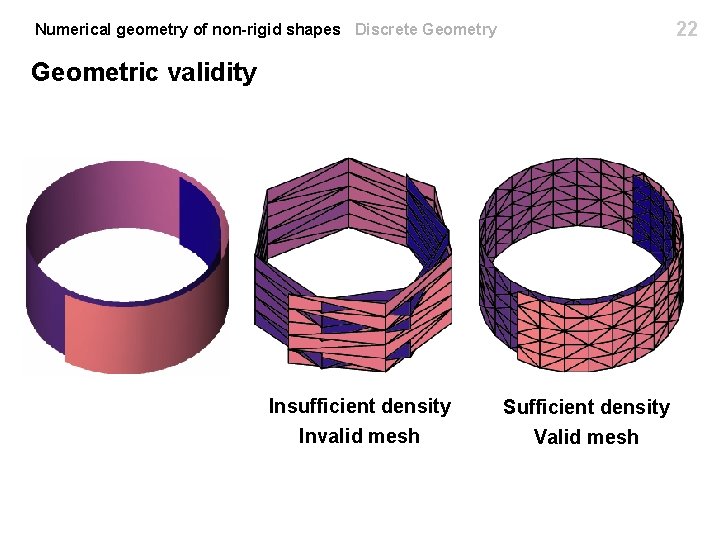
Numerical geometry of non-rigid shapes Discrete Geometry 18 Geometric validity Topologically valid Geometrically invalid Topological validity (manifold mesh) is insufficient! Geometric validity means that the realization of the triangular mesh does not contain self-intersections

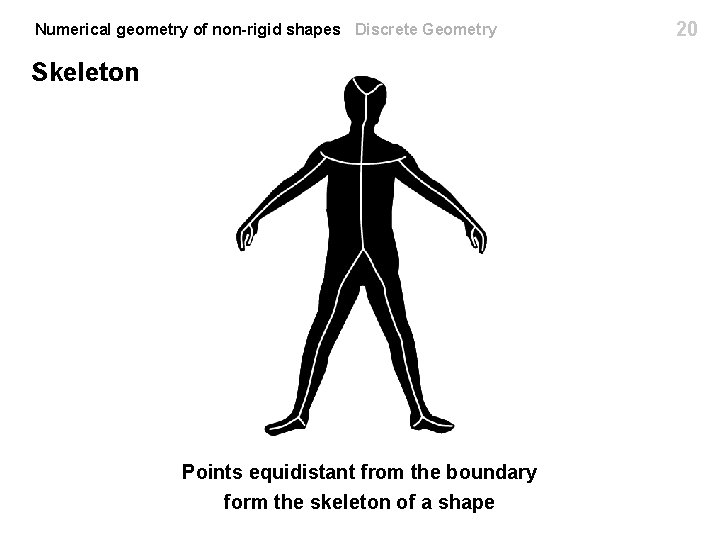
19 Numerical geometry of non-rigid shapes Discrete Geometry Skeleton For a smooth compact surface containing , there exists an envelope ) such that every point is continuously mappable to a unique point on The mapping is realized as the closest point on from Problem when is equidistant from two points on (such points are called medial axis or skeleton of If the mesh is contained in the envelope (does not intersect the medial axis), it is valid (open set in )

Numerical geometry of non-rigid shapes Discrete Geometry Skeleton Points equidistant from the boundary form the skeleton of a shape 20

21 Numerical geometry of non-rigid shapes Discrete Geometry Local feature size Distance from point on to the medial axis of is called the local feature size, denoted Local feature size related to curvature (not an intrinsic property!) [Amenta&Bern, Leibon&Letscher]: if the surface is sampled such that for every that an open ball of radius contains a point of , it is guaranteed does not intersect the medial axis of Conclusion: there exists sufficiently dense sampling guaranteeing that is geometrically valid

22 Numerical geometry of non-rigid shapes Discrete Geometry Geometric validity Insufficient density Invalid mesh Sufficient density Valid mesh

23 Numerical geometry of non-rigid shapes Discrete Geometry Approximation quality How well does the mesh approximate the underlying surface n Sampling quality n Topological equivalence (manifold meshes) n Geometric properties such as area, normals, etc. computed on are close to those computed on ?

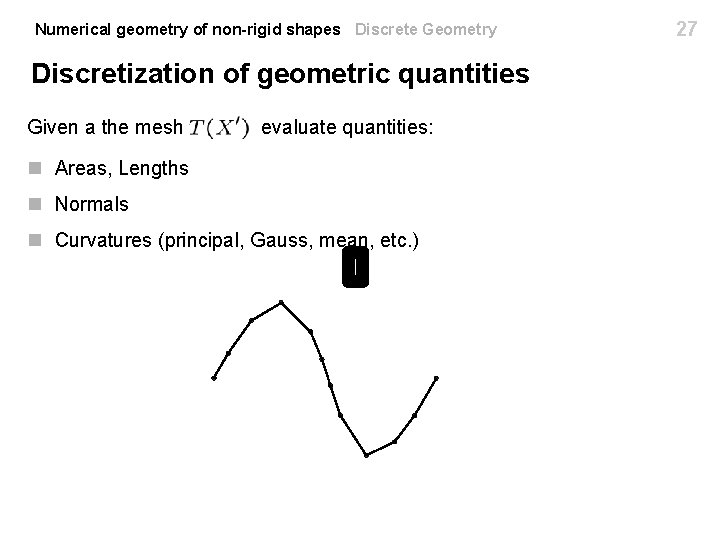
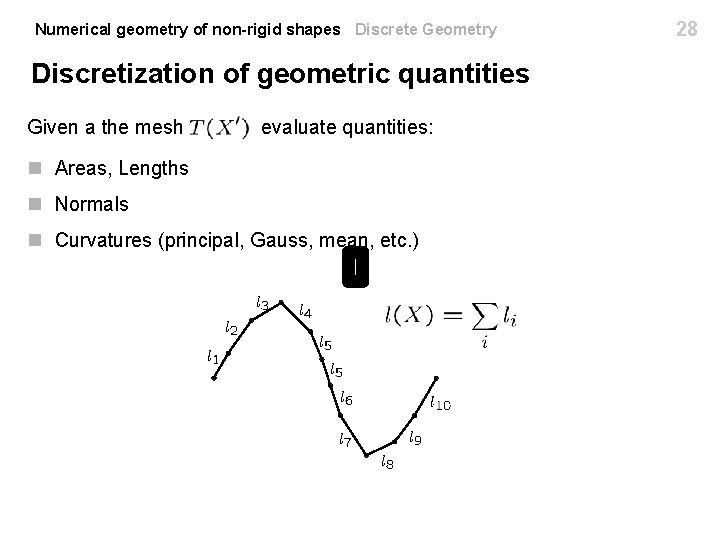
Numerical geometry of non-rigid shapes Discrete Geometry Discretization of geometric quantities Given a the mesh n Areas, Lengths evaluate quantities: Integral n Normals n Curvatures (principal, Gauss, mean, etc. ) Differential 24

Numerical geometry of non-rigid shapes Discrete Geometry Discretization of geometric quantities Given a the mesh evaluate quantities: n Areas, Lengths n Normals n Curvatures (principal, Gauss, mean, etc. ) 25

Numerical geometry of non-rigid shapes Discrete Geometry Discretization of geometric quantities Given a the mesh evaluate quantities: n Areas, Lengths n Normals n Curvatures (principal, Gauss, mean, etc. ) 26

Numerical geometry of non-rigid shapes Discrete Geometry Discretization of geometric quantities Given a the mesh evaluate quantities: n Areas, Lengths n Normals n Curvatures (principal, Gauss, mean, etc. ) 27

Numerical geometry of non-rigid shapes Discrete Geometry Discretization of geometric quantities Given a the mesh evaluate quantities: n Areas, Lengths n Normals n Curvatures (principal, Gauss, mean, etc. ) 28

Numerical geometry of non-rigid shapes Discrete Geometry Discretization of geometric quantities Given a the mesh evaluate quantities: n Areas, Lengths n Normals n Curvatures (principal, Gauss, mean, etc. ) 29

Numerical geometry of non-rigid shapes Discrete Geometry Discretization of geometric quantities Given a the mesh evaluate quantities: n Areas, Lengths n Normals n Curvatures (principal, Gauss, mean, etc. ) 30

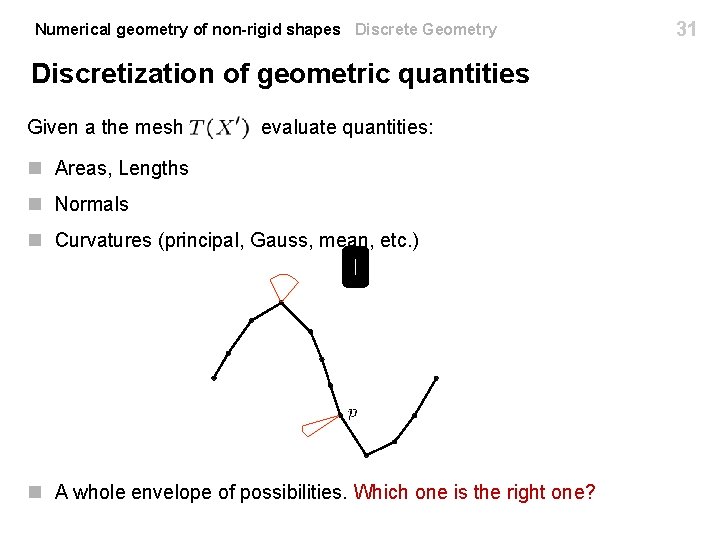
Numerical geometry of non-rigid shapes Discrete Geometry Discretization of geometric quantities Given a the mesh evaluate quantities: n Areas, Lengths n Normals n Curvatures (principal, Gauss, mean, etc. ) n A whole envelope of possibilities. Which one is the right one? 31

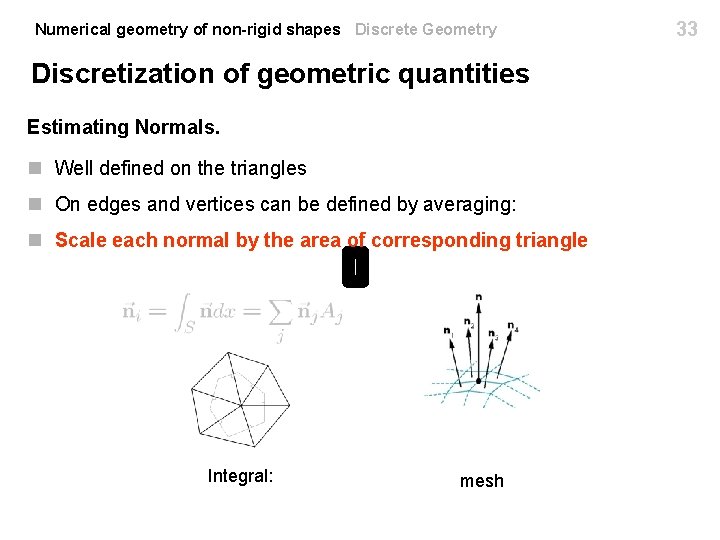
Numerical geometry of non-rigid shapes Discrete Geometry Discretization of geometric quantities Hundreds of methods for estimating differential information. n Case specific. n Try to preserve essential properties of these quantities. n Express them in terms of integral ones. Averaging. Local Regions smooth surface mesh 32

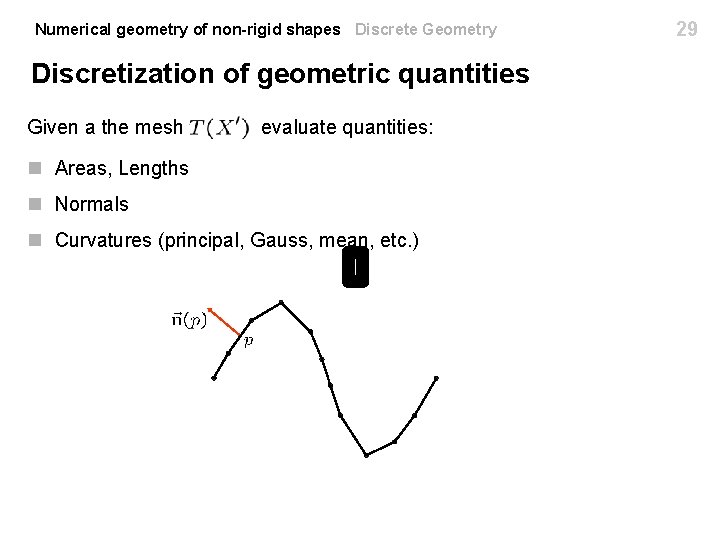
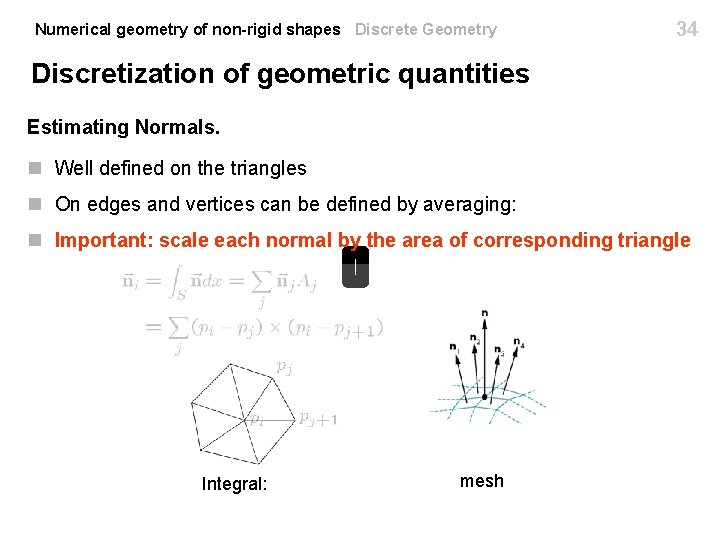
Numerical geometry of non-rigid shapes Discrete Geometry Discretization of geometric quantities Estimating Normals. n Well defined on the triangles n On edges and vertices can be defined by averaging: n Scale each normal by the area of corresponding triangle Integral: mesh 33

Numerical geometry of non-rigid shapes Discrete Geometry 34 Discretization of geometric quantities Estimating Normals. n Well defined on the triangles n On edges and vertices can be defined by averaging: n Important: scale each normal by the area of corresponding triangle Integral: mesh

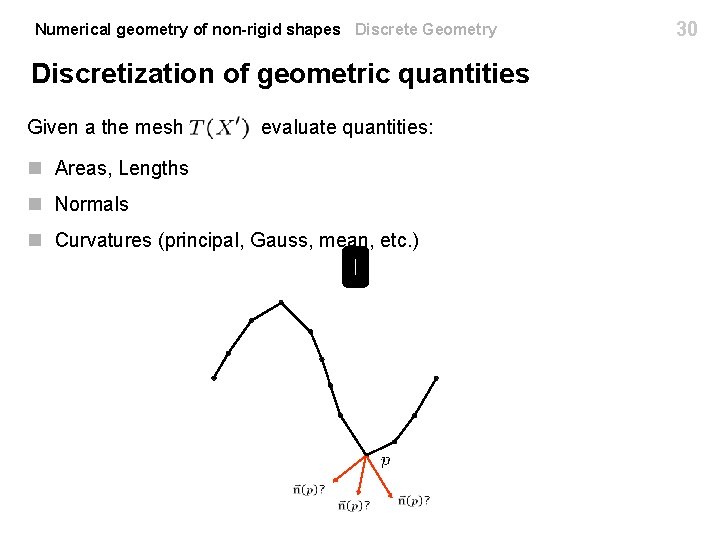
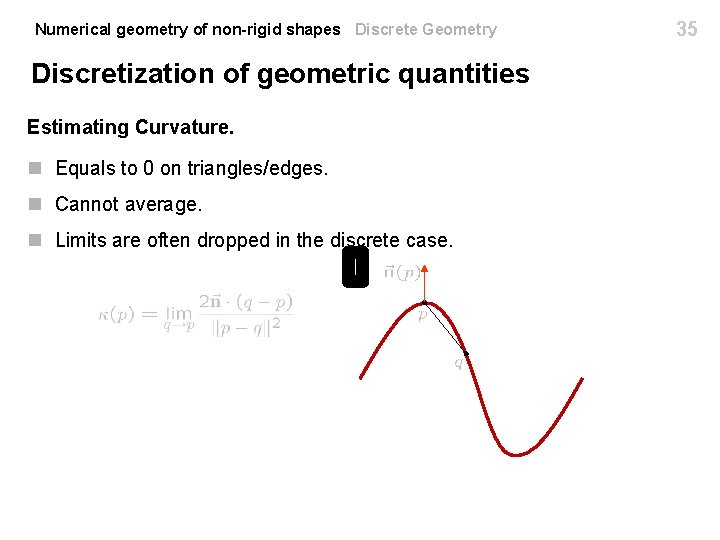
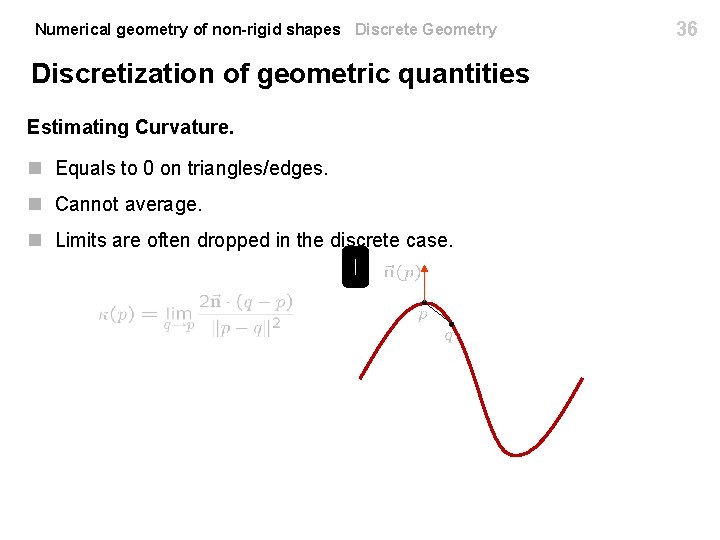
Numerical geometry of non-rigid shapes Discrete Geometry Discretization of geometric quantities Estimating Curvature. n Equals to 0 on triangles/edges. n Cannot average. n Limits are often dropped in the discrete case. 35

Numerical geometry of non-rigid shapes Discrete Geometry Discretization of geometric quantities Estimating Curvature. n Equals to 0 on triangles/edges. n Cannot average. n Limits are often dropped in the discrete case. 36

Numerical geometry of non-rigid shapes Discrete Geometry Discretization of geometric quantities Estimating Curvature. n Equals to 0 on triangles/edges. n Cannot average. n Limits are often dropped in the discrete case. Can be extended to 3 D as well. [Taubin ’ 95] 37

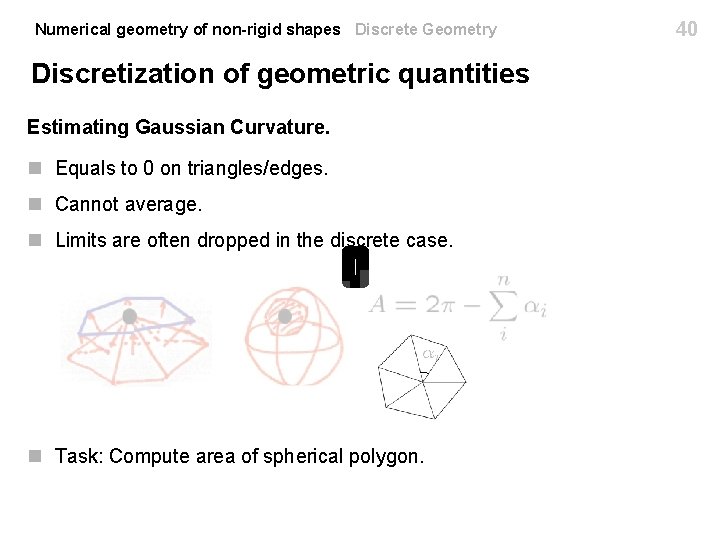
Numerical geometry of non-rigid shapes Discrete Geometry Discretization of geometric quantities Estimating Gaussian Curvature. n Equals to 0 on triangles/edges. n Cannot average. n Limits are often dropped in the discrete case. 38

Numerical geometry of non-rigid shapes Discrete Geometry Discretization of geometric quantities Estimating Gaussian Curvature. n Equals to 0 on triangles/edges. n Cannot average. n Limits are often dropped in the discrete case. n Task: Compute area of spherical polygon. 39

Numerical geometry of non-rigid shapes Discrete Geometry Discretization of geometric quantities Estimating Gaussian Curvature. n Equals to 0 on triangles/edges. n Cannot average. n Limits are often dropped in the discrete case. n Task: Compute area of spherical polygon. 40

41 Numerical geometry of non-rigid shapes Discrete Geometry Approximation quality How well does the mesh approximate the underlying surface n Sampling quality n Topological equivalence (manifold meshes) n Geometric properties such as area, normals, etc. computed on are close to those computed on ?

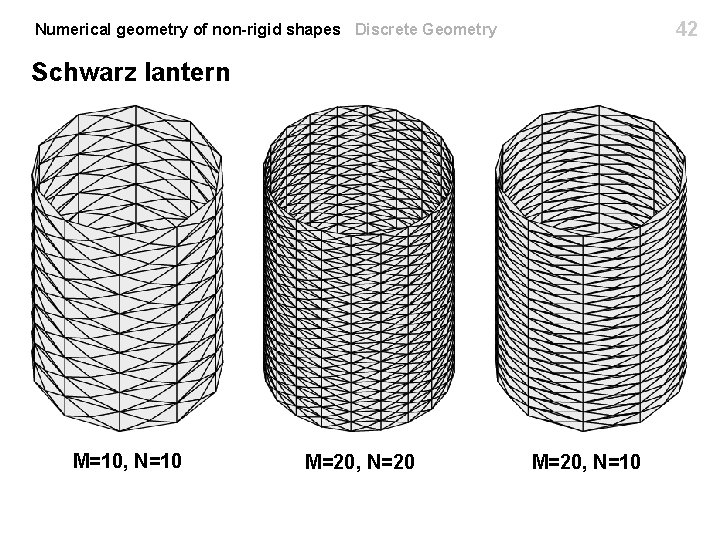
42 Numerical geometry of non-rigid shapes Discrete Geometry Schwarz lantern M=10, N=10 M=20, N=20 M=20, N=10

43 Numerical geometry of non-rigid shapes Discrete Geometry Schwarz lantern Set . Then, in the limit Reason: triangles become infinitely thin [Morvan & Thibert 2002]: if the triangulation is sufficiently fat, the area approximation error is bounded Hermann Schwarz (1843 -1921)

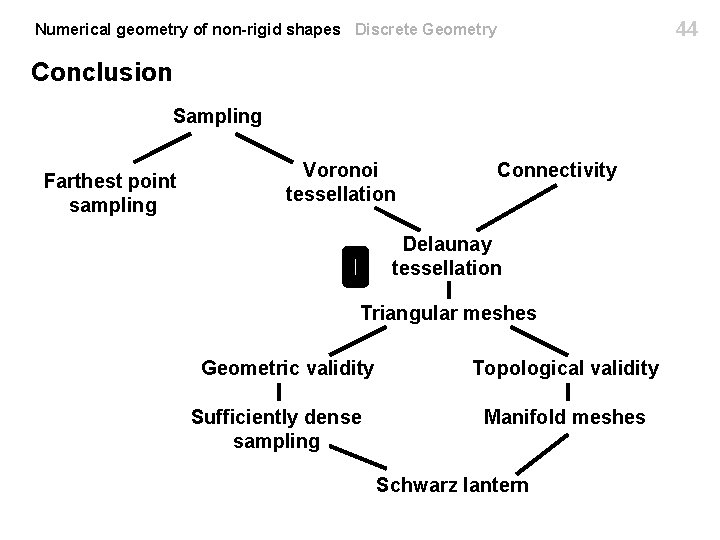
44 Numerical geometry of non-rigid shapes Discrete Geometry Conclusion Sampling Farthest point sampling Voronoi tessellation Connectivity Delaunay tessellation Triangular meshes Geometric validity Sufficiently dense sampling Topological validity Manifold meshes Schwarz lantern