Numerical Differentiation JyunMing Chen 1 Contents Forward Backward

Numerical Differentiation Jyun-Ming Chen 1

Contents • Forward, Backward, Central Difference • Richardson Extrapolation 2

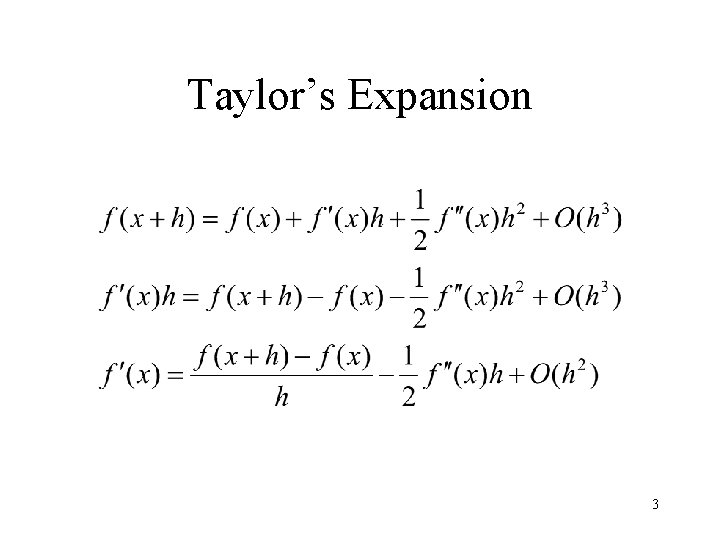
Taylor’s Expansion 3

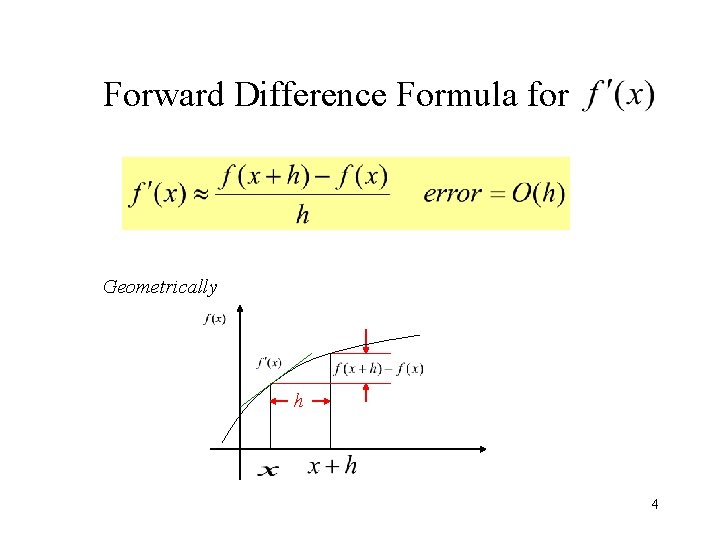
Forward Difference Formula for Geometrically h 4

Backward Difference Formula for Similarly Geometrically h 5

Central Difference Formula for –) 6

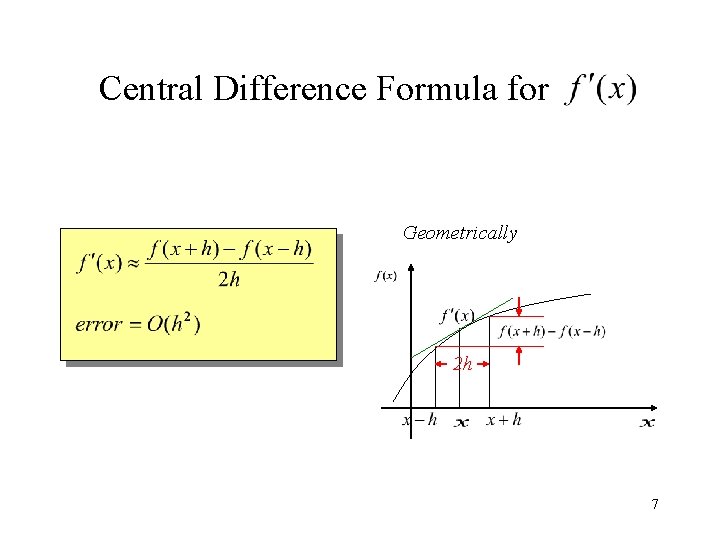
Central Difference Formula for Geometrically 2 h 7

Example , Calculate f’(1) using FD, BD, CD 8

Example (cont) FD: h=0. 1 h=0. 05 BD: h=0. 1 h=0. 05 CD: h=0. 1 h=0. 05 9

Example (cont) • Remarks: – FD, BD, CD each involves 2 function calls, 1 subtraction, and 1 division: same computation time – CD is the most accurate (hence, the most recommended method) – However, sometimes, CD cannot be applied 10

Forward Difference Formula for – 2 ） 11

Backward Difference Formula for – 2 ） 12

Central Difference Formula for +) Similar remark on the selection of FD|BD|CD applies for f”(x) 13

More Accurate FD Formula for 14

More Accurate FD Formula (cont) • Better accuracy can be achieved using this formula • But, it involves more computations: – 3 function calls, two +/–, one division • Trade-off: – More computation is the price you paid for better accuracy • Similar idea applies to more accurate BD formula 15

Richardson Extrapolation Idea: • exact = computed+ error • The truncation error is of the form: chk – where c is some constant • Use different h to estimate the truncation error • Use extrapolation to get more accurate result 16

Richardson Extrapolation (cont) • Example: CD for f’(x) • Using Different h (h 1, h 2)： • c 1 and c 2 could be different 17

Richardson Extrapolation (cont) • If 18

Example • f(x) = x 3. Use CD with Richardson extrapolation to compute f’(1) Magic? Coincidence ? 19

Revisit CD Formula for –) Change notation: 20

Error Analysis Assuming Eliminate a 1 to get better accuracy 21

Error Analysis (cont) 4 –) O(h 4) 22

Revisit Previous Example • f(x) = x 3. Use CD with Richardson extrapolation to compute f’(1) • a 2 involves f(5)(x), hence, the exact solution is no surprise. 23

Remark • How much effort did we use to get this level of accuracy? – F(h): f(x+h), f(x-h); one –, one – F(h/2): f(x+h/2), f(x-h/2); one –, one – R. E. : two , one – 24

Summary (Textbook p. 373) 25

26

http//: earendil. ath. cx/content/academic/numeralysis 1. doc אקסטרפולציית ריצ'רדסון לביטול איבר השגיאה המוביל 27