Numerical Analysis of Bubble Powered Micropump Gad A

Numerical Analysis of Bubble Powered Micropump Gad A. Pinhasi Matan Pe’er and Amos Ullmann COMSOL CONFERENCE 2019 Cambridge, September 24– 26 1
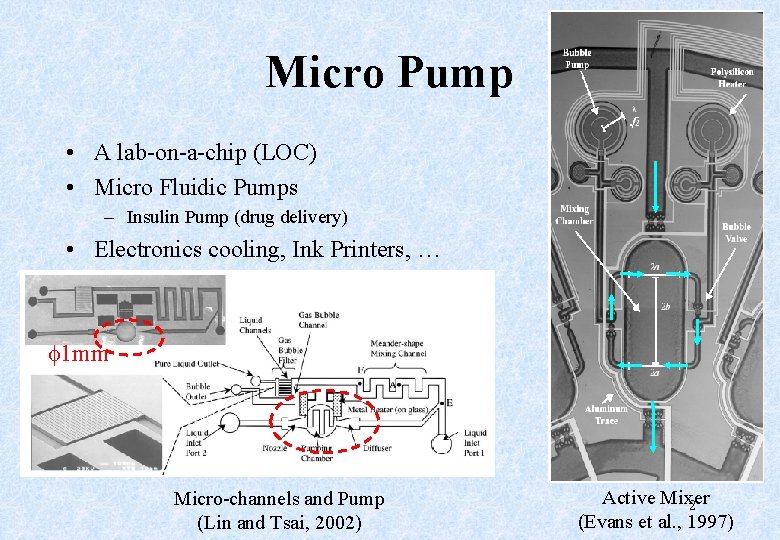
Micro Pump • A lab-on-a-chip (LOC) • Micro Fluidic Pumps – Insulin Pump (drug delivery) • Electronics cooling, Ink Printers, … 1 mm Micro-channels and Pump (Lin and Tsai, 2002) Active Mixer 2 (Evans et al. , 1997)

Bubble Micro-Pump • Driving force – Bubble formation, growth and collapse – Vapor volume change • Flow control – Diffuser/Nozzle • Unsteady Pumping flow – Pulsing flow • No moving parts Tsai and Lin (2002) Jung and Kwak (2007) 3

Bubble Lifetime Cycle • Heating – “Waiting” Time • Bubble formation: – Stable bubble criterion – Nucleation • Bubble growth – Inertia Controlled – Diffusion Controlled • Collapse • Problem: Discontinuity in the flow field in time Deniray and Kim (2004) 4

The Objective • Developing a numerical model to simulate the operation of a micro-pump driven by bubble formation and growth. • Sub-models: – – Initial liquid heating, Formation of a critical bubble, Bubble growth and collapse The liquid flow through the nozzles system. 5

Basic Assumptions • Laminar flow • Heating with constant heat flux. – Duty cycle (= 80%) q” th DC=th/Tc Tc t • Initial liquid temperature: Ambient • Initial Hemispherical critical bubble on the wall • Case Study: – Displacement Pump: 2 D, 3 D analysis – Bubble growth simulation: 2 D spherical – Bubble Pump: 2 D analysis 6

Conservation Equations • Continuity • Momentum: NS Eq. • Heat Eq. : Convection • Heat and Mass Transfer at the Boundary – Phase Change – Moving boundary Liquid Vapor Evaporation me ” Heat q” 7
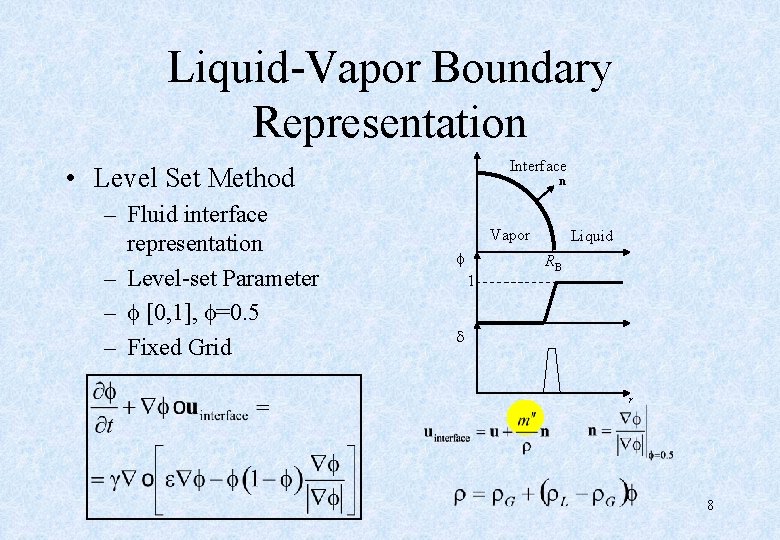
Liquid-Vapor Boundary Representation Interface • Level Set Method – Fluid interface representation – Level-set Parameter – [0, 1], =0. 5 – Fixed Grid n Vapor 1 Liquid RB d r 8
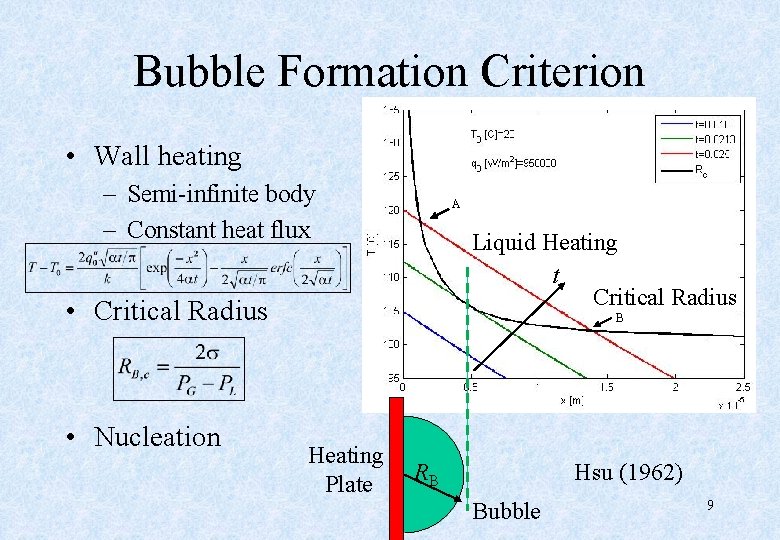
Bubble Formation Criterion • Wall heating – Semi-infinite body – Constant heat flux A Liquid Heating t Critical Radius • Nucleation B Heating Plate Hsu (1962) RB Bubble 9
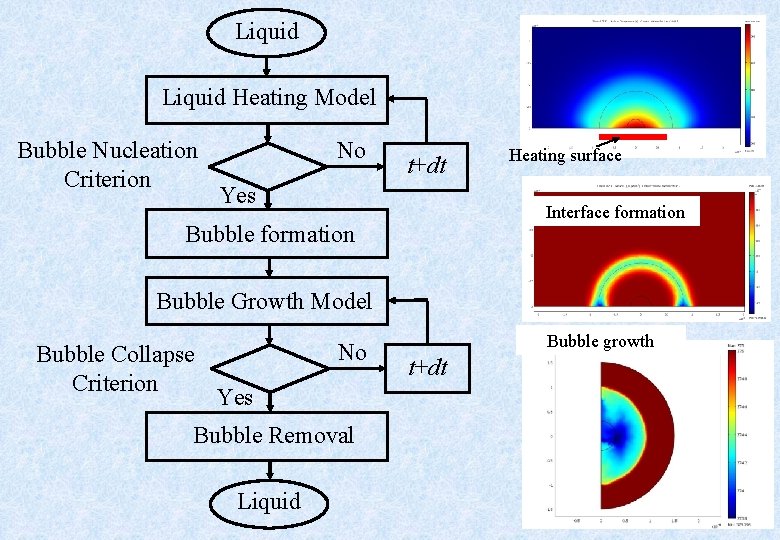
Liquid Heating Model Bubble Nucleation Criterion No t+dt Yes Heating surface Interface formation Bubble Growth Model Bubble Collapse Criterion No Bubble growth t+dt Yes Bubble Removal Liquid 10

The CFD Tools • MATLAB Based – Main program – Script (MATLAB) • COMSOL Multiphysics – Physics: • Laminar flow • Heat Transfer • Fixed Grid Boundary problem: Level set – Grid generator – Solver – Post Proceeding COMSOL Multiphysics and the Live. Link for MATLAB Combine user code and software functions and solvers: 11

Results 1. 2. 3. 4. Diffuser/Nozzle Characteristics Displacement Pump Bubble growth Bubble pump 12
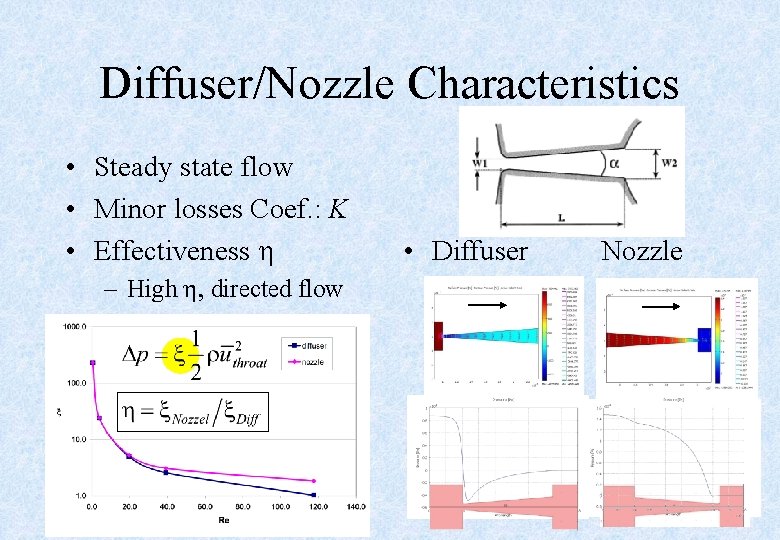
Diffuser/Nozzle Characteristics • Steady state flow • Minor losses Coef. : K • Effectiveness h • Diffuser Nozzle – High h, directed flow 13
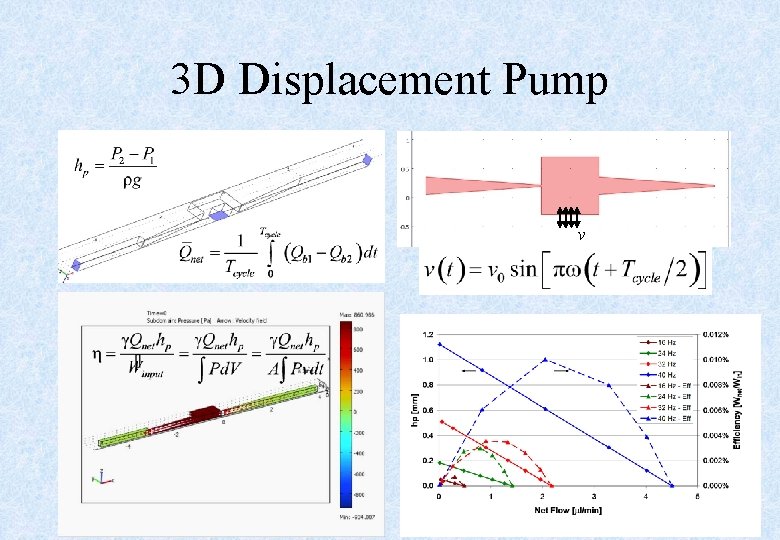
3 D Displacement Pump v 14
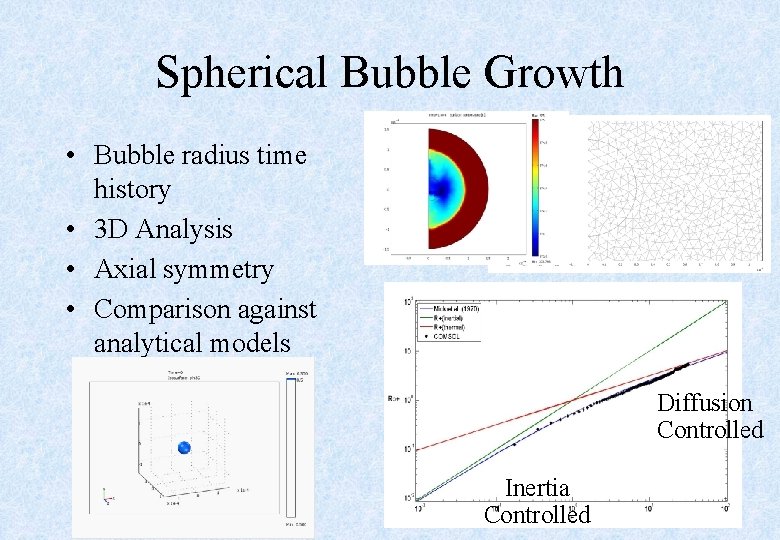
Spherical Bubble Growth • Bubble radius time history • 3 D Analysis • Axial symmetry • Comparison against analytical models Diffusion Controlled Inertia Controlled 15
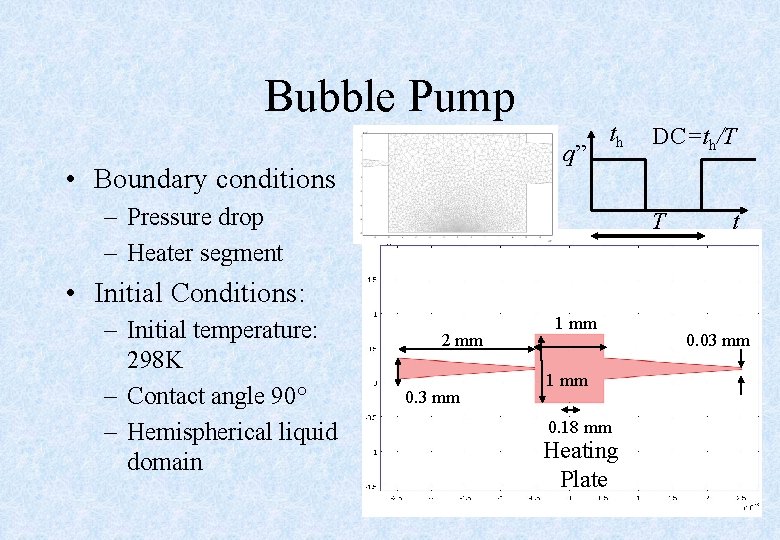
Bubble Pump q” • Boundary conditions th – Pressure drop – Heater segment DC=th/T T t • Initial Conditions: – Initial temperature: 298 K – Contact angle 90 – Hemispherical liquid domain 2 mm 0. 3 mm 1 mm 0. 03 mm 1 mm 0. 18 mm Heating Plate 16
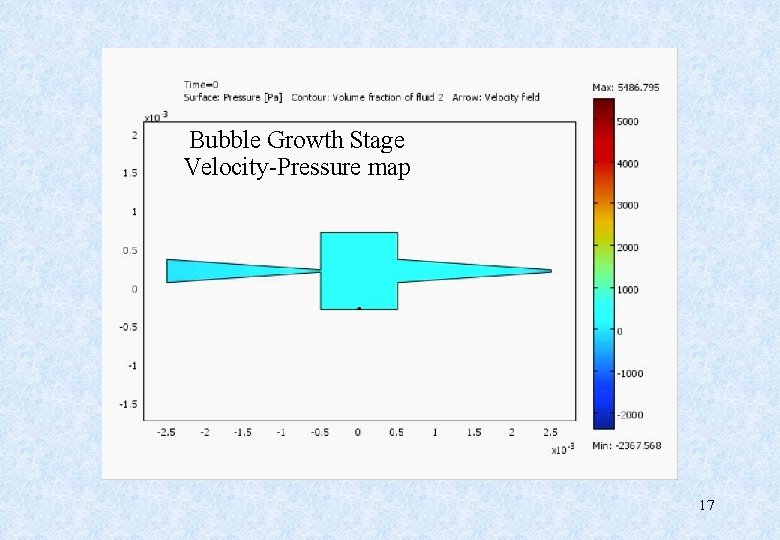
Bubble Growth Stage Velocity-Pressure map 17
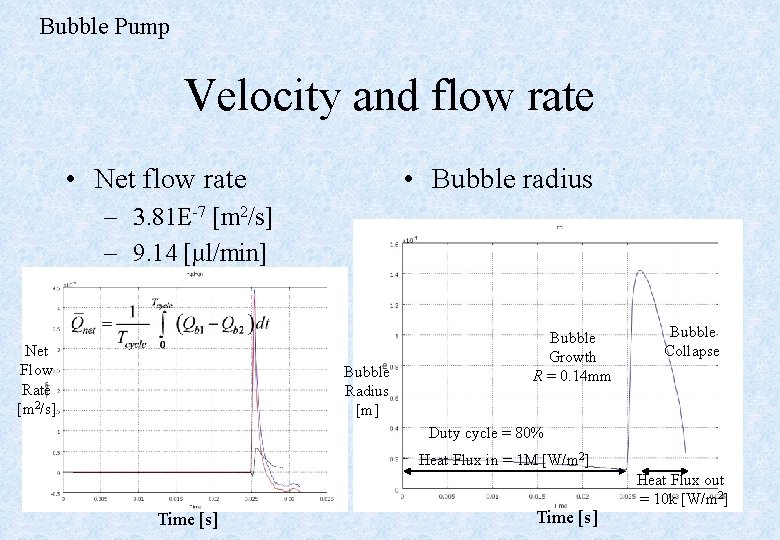
Bubble Pump Velocity and flow rate • Net flow rate • Bubble radius – 3. 81 E-7 [m 2/s] – 9. 14 [µl/min] Net Flow Rate [m 2/s] Bubble Radius [m] Bubble Growth R = 0. 14 mm Bubble Collapse Duty cycle = 80% Heat Flux in = 1 M [W/m 2] Time [s] Heat Flux out 2 = 10 k [W/m 18 ]
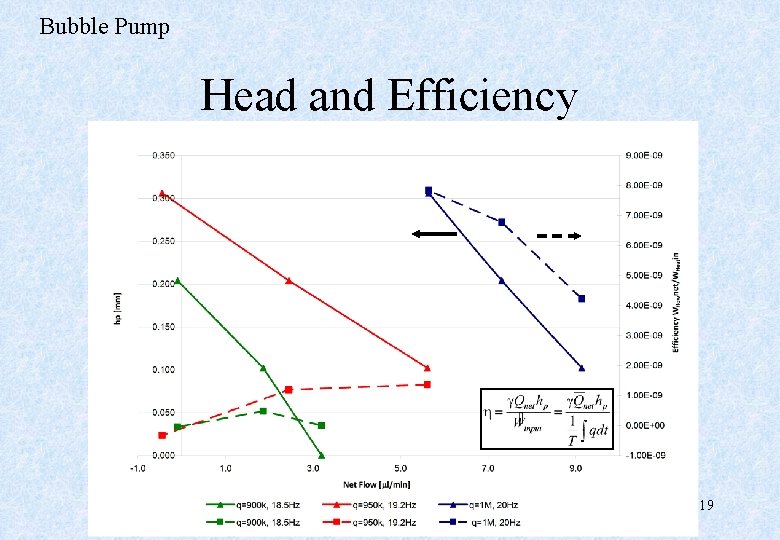
Bubble Pump Head and Efficiency 19

Summery • A numerical model was developed to simulate the operation of a micro-pump driven by bubble formation and growth. • The model solves the time dependent conservation equation for viscid fluid: mass, momentum and convection heat transfer. • The Level-Set method is being used to represent the gas-liquid interface. • The analysis is made by using finite element software. COMSOL Multiphysics. • The model was tested against analytical model for diffusive bubble growth. 20
Pinhasi, G. A. , Pe'er, M. and Ullmann, A. (2019) “Numerical Analysis of Bubble Powered Micropump”, Proceedings of COMSOL Conference 2019, Cambridge, September 24– 26. 21

22
- Slides: 22