Numerical Analysis Lecture 45 Summing up NonLinear Equations

Numerical Analysis Lecture 45

Summing up

Non-Linear Equations

Bisection Method (Bolzano) Regula-Falsi Method of iteration Newton - Raphson Method Muller’s Method Graeffe’s Root Squaring Method

In the method of False Position, the first approximation to the root of f (x) = 0 is given by (2. 2) Here f (xn-1) and f (xn+1) are of opposite sign. Successive approximations to the root of f (x) = 0 is given by Eq. (2. 2).

METHOD OF ITERATION can be applied to find a real root of the equation f (x) = 0 by rewriting the same in the form,

In Newton – Raphson Method successive approximations x 2, x 3, …, xn to the root are obtained from N-R Formula

Secant Method This sequence converges to the root ‘b’ of f (x) = 0 i. e. f( b ) = 0.

The Secant method converges faster than linear and slower than Newton’s quadratic.

In Muller’s Method we can get a better approximation to the root, by using

Where we defined

Systems of Linear Equations

Gaussian Elimination Gauss-Jordon Elimination Crout’s Reduction Jacobi’s Gauss- Seidal Iteration Relaxation Matrix Inversion

In Gaussian Elimination method, the solution to the system of equations is obtained in two stages. i)the given system of equations is reduced to an equivalent upper triangular form using elementary transformations ii)the upper triangular system is solved using back substitution procedure

Gauss-Jordon method is a variation of Gaussian method. In this method, the elements above and below the diagonal are simultaneously made zero

In Crout’s Reduction Method the coefficient matrix [A] of the system of equations is decomposed into the product of two matrices [L] and [U], where [L] is a lower-triangular matrix and [U] is an upper-triangular matrix with 1’s on its main diagonal.

For the purpose of illustration, consider a general matrix in the form

Jacobi’s Method is an iterative method, where initial approximate solution to a given system of equations is assumed and is improved towards the exact solution in an iterative way.

In Jacobi’s method, the (r + 1)th approximation to the above system is given by Equations

Here we can observe that no element of replaces entirely for the next cycle of computation.

In Gauss-Seidel method, the corresponding elements of replaces those of as soon as they become available. It is also called method of Successive Displacement.

The Relaxation Method is also an iterative method and is due to Southwell.

Eigen Value Problems Power Method Jcobi’s Method

In Power Method the result looks like Here, is the desired largest eigen value and is the corresponding eigenvector.

Interpolation

Finite Difference Operators Newton’s Forward Difference Interpolation Formula Newton’s Backward Difference Interpolation Formula Lagrange’s Interpolation Formula Divided Differences Interpolation in Two Dimensions Cubic Spline Interpolation

Finite Difference Operators Forward Differences Backward Differences Central Difference

Thus Similarly

Shift operator, E

The inverse operator is defined as Similarly, -1 E

Average Operator,

Differential Operator, D

Important Results

The Newton’s forward difference formula for interpolation, which gives the value of f (x 0 + ph) in terms of f (x 0) and its leading differences.

An alternate expression is

Newton’s Backward difference formula is,

Alternatively, this formula can also be written as Here

The Lagrange’s formula for interpolation

Newton’s divided difference interpolation formula can be written as

Where the first order divided difference is defined as

Numerical Differentiation and Integration

We expressed D in terms of ∆ :

Using backward difference operator , we have On expansion, we have

Using Central difference Operator Differentiation Using Interpolation Richardson’s Extrapolation

Thus, is approximated by which is given by

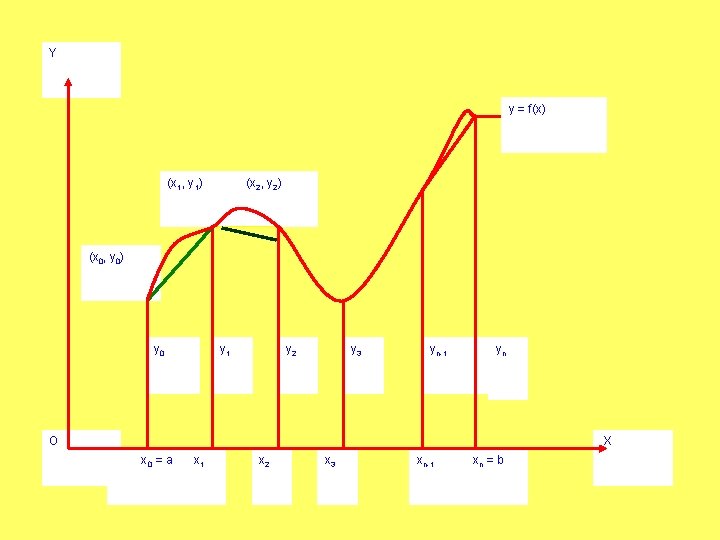
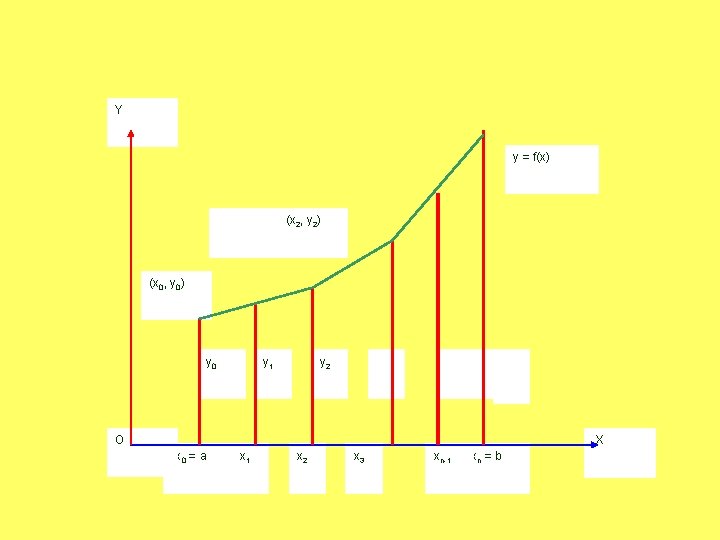
Basic Issues in Integration What does an integral represent? = AREA = VOLUME

Y y = f(x) (x 1, y 1) (x 2, y 2) (x 0, y 0) y 0 y 1 y 2 y 3 yn-1 yn O X x 0 = a x 1 x 2 x 3 xn-1 xn = b

Y y = f(x) (x 2, y 2) (x 0, y 0) y 0 y 1 y 2 O X x 0 = a x 1 x 2 x 3 xn-1 xn = b

TRAPEZOIDAL RULE

DOUBLE INTEGRATION We described procedure to evaluate numerically a double integral of the form

Differential Equations

Taylor Series Euler Method Runge-Kutta Method Predictor Corrector Method

In Taylor’s series we expanded y (t ) by Taylor’s series about the point t = t 0 and obtain

In Euler Method we obtained the solution of the differential equation in the form of a recurrence relation

We derived the recurrence relation Which is the modified Euler’s method.

The fourth-order R-K method was described as

where

In general, Milne’s predictorcorrector pair can be written as

This is known as Adam’s predictor formula. Alternatively, it can be written as

Numerical Analysis Lecture 45