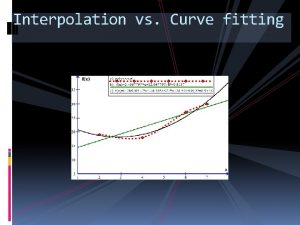
Numerical Analysis Interpolation Hanyang University JongIl Park Fitting

Numerical Analysis – Interpolation Hanyang University Jong-Il Park

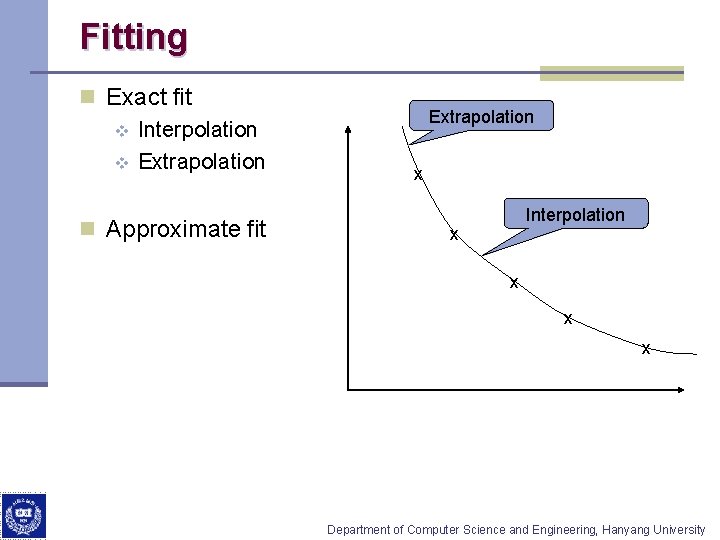
Fitting n Exact fit v Interpolation v Extrapolation n Approximate fit Extrapolation x Interpolation x x Department of Computer Science and Engineering, Hanyang University

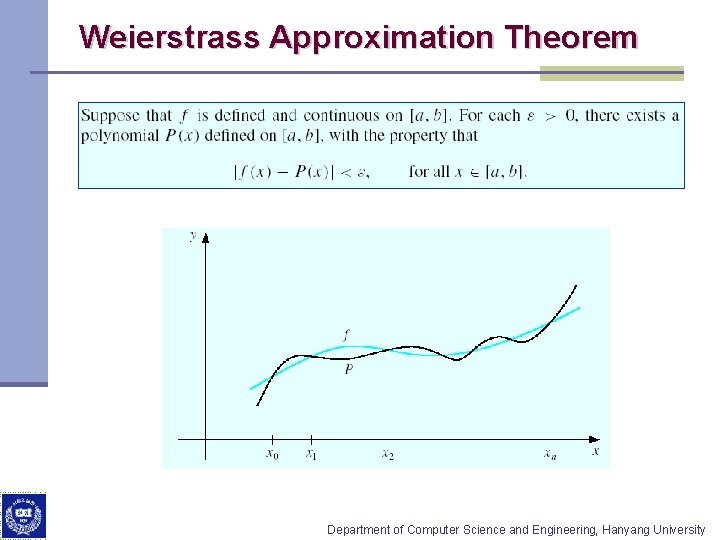
Weierstrass Approximation Theorem Department of Computer Science and Engineering, Hanyang University

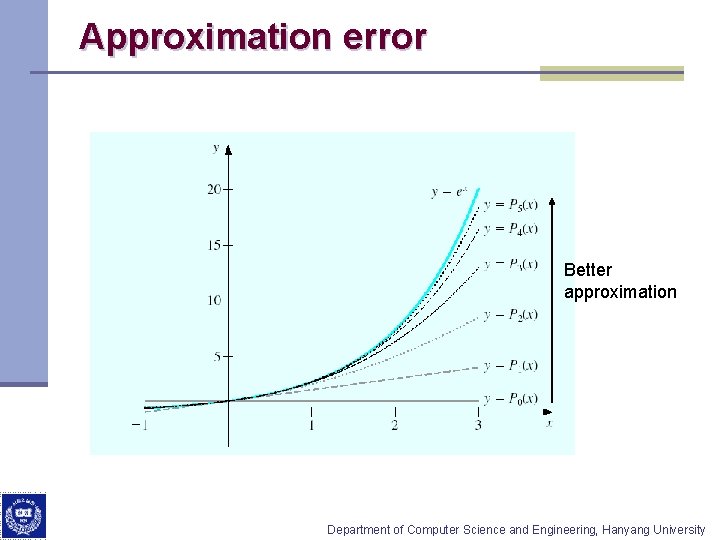
Approximation error Better approximation Department of Computer Science and Engineering, Hanyang University

Lagrange Interpolating Polynomial Department of Computer Science and Engineering, Hanyang University

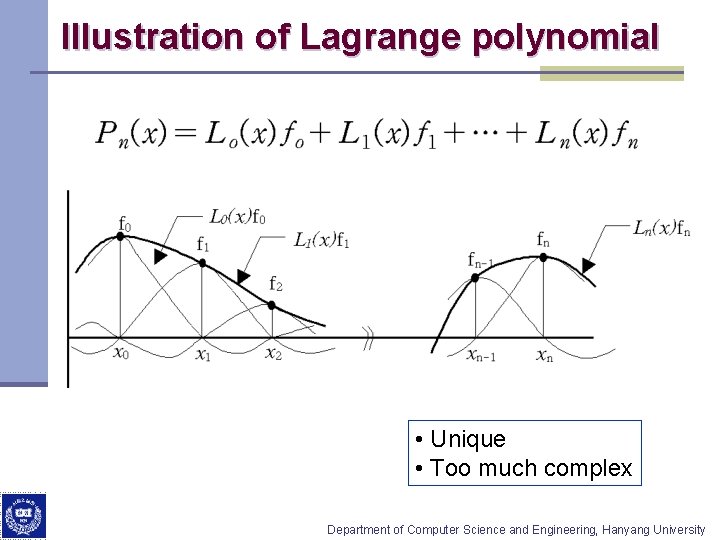
Illustration of Lagrange polynomial • Unique • Too much complex Department of Computer Science and Engineering, Hanyang University

Error analysis for intpl. polynml(I) Department of Computer Science and Engineering, Hanyang University

Error analysis for intpl. polynml(II) Department of Computer Science and Engineering, Hanyang University

Differences n Difference v Forward difference : v Backward difference : v Central difference : f Department of Computer Science and Engineering, Hanyang University

Divided Differences ; 1 st order divided difference ; 2 nd order divided difference Department of Computer Science and Engineering, Hanyang University

N-th divided difference Department of Computer Science and Engineering, Hanyang University

Newton’s Intpl. Polynomials(I) Department of Computer Science and Engineering, Hanyang University

Newton’s Intpl. Polynomials(II) Department of Computer Science and Engineering, Hanyang University

Newton’s Forward Difference Interpolating Polynomials(I) v Equal Interval h v Derivation n=1 n=2 Department of Computer Science and Engineering, Hanyang University

Newton’s Forward Difference Interpolating Polynomials(II) Generalization Binomial coef. v Error Analysis Department of Computer Science and Engineering, Hanyang University

Intpl. of Multivariate Function • Successive univariate polynomial • Direct mutivariate polynomial 1 2 1 Successive univariate direct multivariate Department of Computer Science and Engineering, Hanyang University

Inverse Interpolation = finding v x(f) Utilization of Newton’s polynomial Solve for x 1 st approximation 2 nd approximation Repeat until a convergence Department of Computer Science and Engineering, Hanyang University

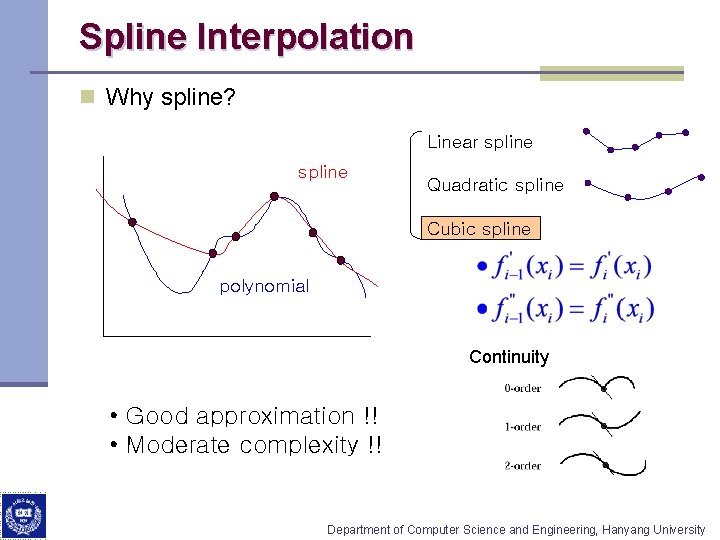
Spline Interpolation n Why spline? Linear spline Quadratic spline Cubic spline polynomial Continuity • Good approximation !! • Moderate complexity !! Department of Computer Science and Engineering, Hanyang University

Cubic spline interpolation(I) n Cubic Spline Interpolation at an interval 4 unknowns for each interval 4 n unknowns for n intervals Conditions 1) n 2) n 3) continuity of f’ n-1 4) continuity of f’’ n-1 Department of Computer Science and Engineering, Hanyang University

Cubic spline interpolation(II) n Determining boundary condition Method 1 : Method 2 : Method 3 : Department of Computer Science and Engineering, Hanyang University

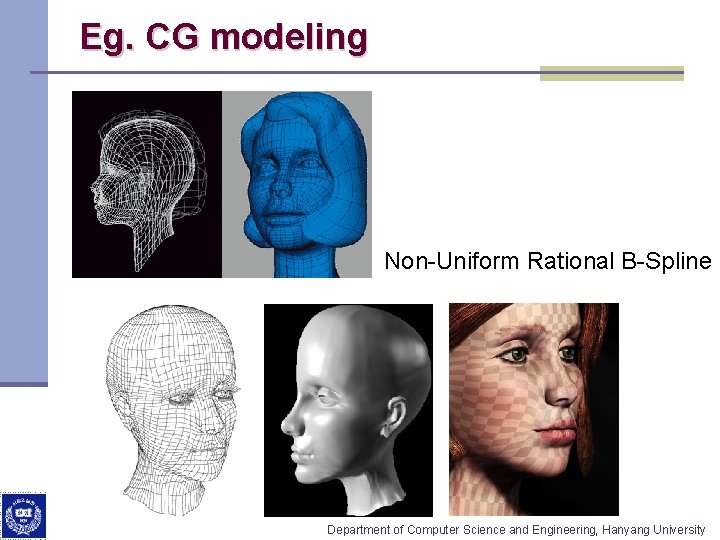
Eg. CG modeling Non-Uniform Rational B-Spline Department of Computer Science and Engineering, Hanyang University