Numerical Analysis Advanced Topics in Root Finding Hanyang

Numerical Analysis - Advanced Topics in Root Finding - Hanyang University Jong-Il Park

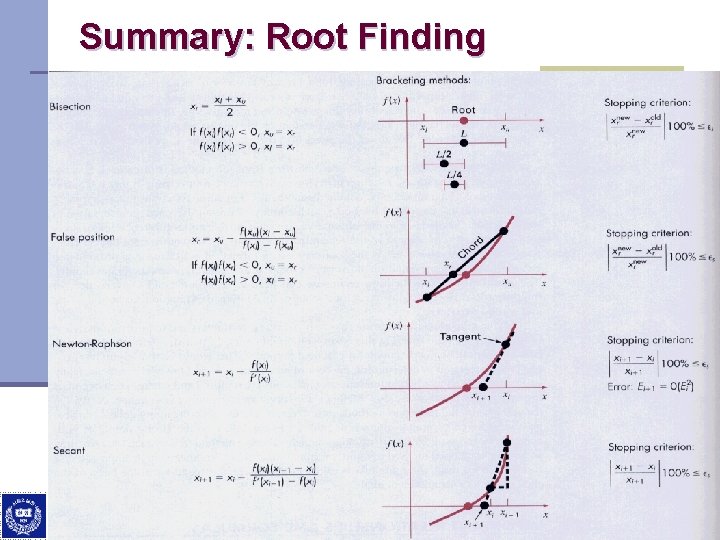
Summary: Root Finding Department of Computer Science and Engineering, Hanyang University

Error analysis of N-R method Taylor series: Newton-Raphson method: --- (1) At the true solution xr : --- (2) (1) (2) : Let Quadratic convergence! Department of Computer Science and Engineering, Hanyang University

Error Analysis of Secant Method n Convergence [Jeeves, 1958] v More efficient than N-R method if the calculation of f’(x) is complex n Modified secant method Department of Computer Science and Engineering, Hanyang University

Multiple roots n Bracketing methods cannot cope with multiple roots n Open methods can find multiple roots But the speed is slow in many cases v f’(x) 0 will cause a problem(divide by zero) f(x) will always reach zero before f’(x) [Ralston and Rabinowitz, 1978] if a zero check for f(x) is incorporated into the program, the computation can be terminated before f’(x) reaches zero v Alternative way using u(x)=f(x)/f’(x) v Department of Computer Science and Engineering, Hanyang University

Polynomial evaluation n Bad method n Worst method n Best method C code Department of Computer Science and Engineering, Hanyang University

Polynomial differentiation or Department of Computer Science and Engineering, Hanyang University

N-th derivatives Department of Computer Science and Engineering, Hanyang University

Polynomial deflation n Multiplication by (x-a) n Synthetic division by (x-a) Department of Computer Science and Engineering, Hanyang University

Bairstow’s method n Deflation method v v v Find r and s such that b 0=b 1=0 Efficient routine using synthetic division exists Good initial guess of r, s is important Complex roots can be evaluated Suitable for root polishing n In Numerical Recipes in C void qroot(); Read Sect. 7. 5. Department of Computer Science and Engineering, Hanyang University

Laguerre method n Deflation method n Algorithm derivation n In Numerical Recipes in C: zroots() calls laguer(); Department of Computer Science and Engineering, Hanyang University

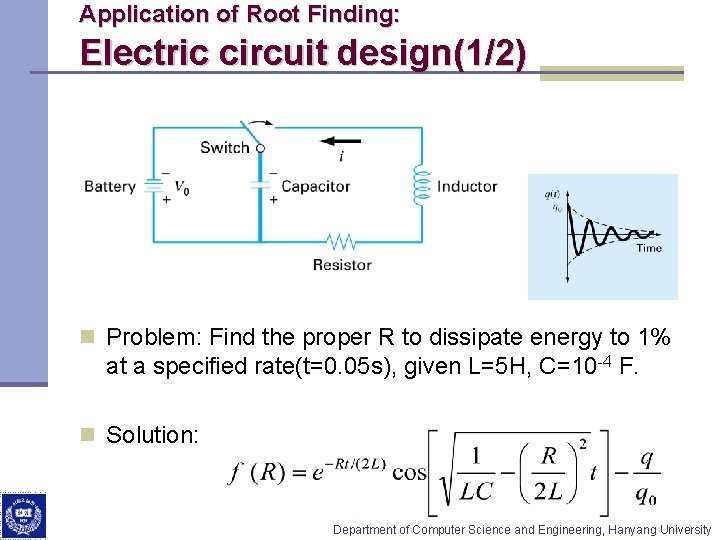
Application of Root Finding: Electric circuit design(1/2) n Problem: Find the proper R to dissipate energy to 1% at a specified rate(t=0. 05 s), given L=5 H, C=10 -4 F. n Solution: Department of Computer Science and Engineering, Hanyang University

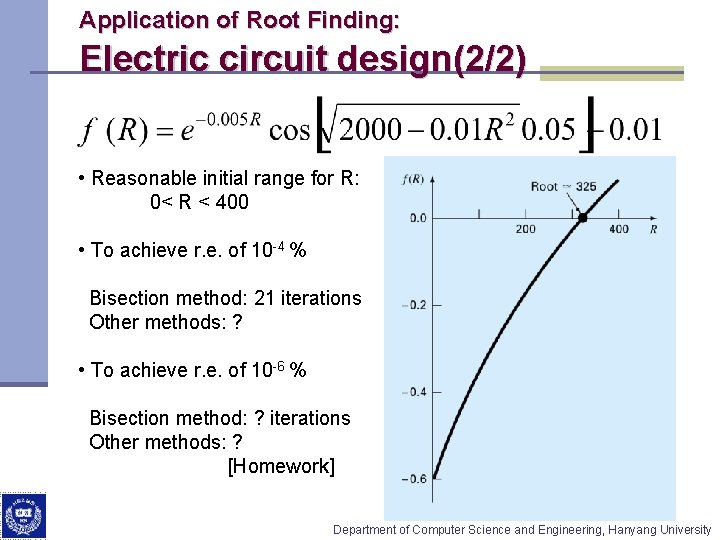
Application of Root Finding: Electric circuit design(2/2) • Reasonable initial range for R: 0< R < 400 • To achieve r. e. of 10 -4 % Bisection method: 21 iterations Other methods: ? • To achieve r. e. of 10 -6 % Bisection method: ? iterations Other methods: ? [Homework] Department of Computer Science and Engineering, Hanyang University

Homework #4 [Due: 10/17] n Find the root of f(R)=0 and the number of iterations when the r. e. =10 -4 and 10 -6 respectively. n Solve the 8 -31, 32 problems: n Explain the concept of “pointer to function” and describe how you use it in your homework #3. Department of Computer Science and Engineering, Hanyang University