Numerical Algorithms Group Mathematics and technology for optimized

Numerical Algorithms Group Mathematics and technology for optimized performance Numerical Software, Market Data and Extreme Events Robert Tong Results Matter. Trust NAG.

Outline • • • Market data Pre-processing Software components Extreme events Example: wavelet analysis of FX spot prices • Implications for software design 2

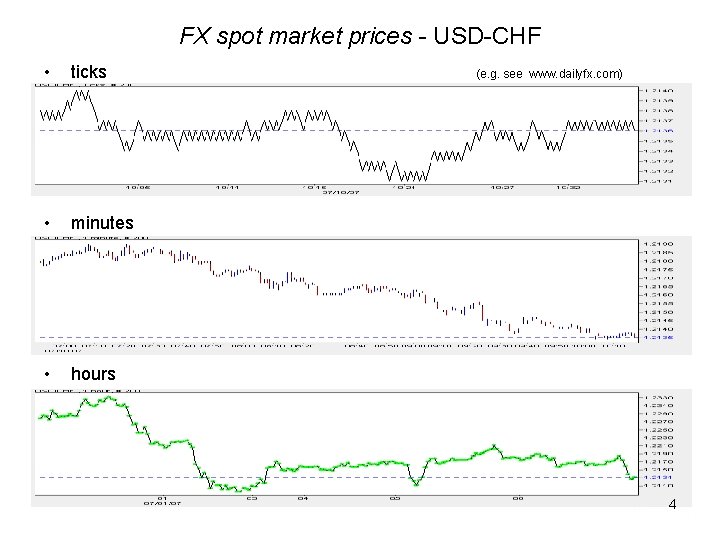
Market data • Tick – as transactions occur, high frequency, irregular in time quote/price with time stamp • Sample tick data at regular times – minute, hour, day, … – low-high price • Bid-ask pairs – FX spot market • Time series – construct from sampled and processed data 3

FX spot market prices - USD-CHF • ticks • minutes • hours (e. g. see www. dailyfx. com) 4

Data cleaning Required to remove errors in data – • • • inputting errors test ticks to check system response repeated ticks copying and re-sending of ticks scaling errors How can false values be reliably identified and rejected ? • what assumptions must be imposed? • elimination of outliers based on an assumed probability distribution 5

Pre-processing • Tick data irregular in time – construct homogeneous time series by interpolation: linear, repeated value • Bid-ask spread – use relative spread • Remove seasonality • Account for holidays Ø Must not introduce spurious structures to data 6

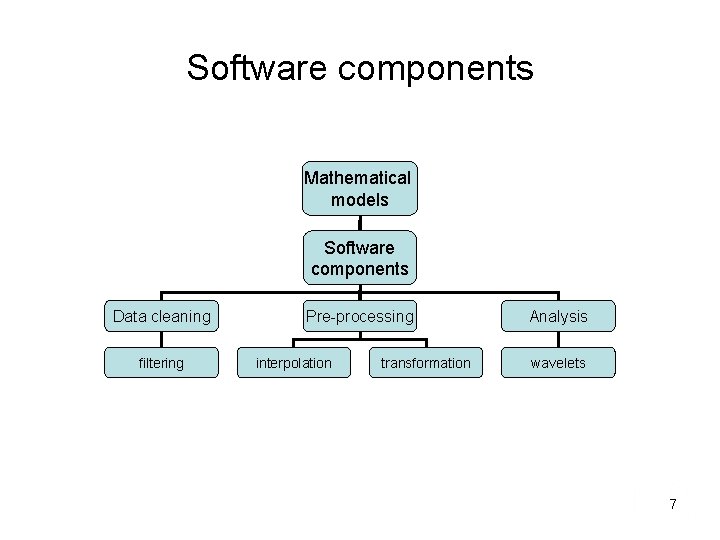
Software components Mathematical models Software components Data cleaning filtering Pre-processing interpolation transformation Analysis wavelets 7

Implementation issues Algorithm design – – – – Stability Accuracy Exception handling Portability Error indicators Documentation These are independent of the problem being solved 8

Extreme events • Weather – storm • Warfare – explosion • Markets – crash Software – How should it respond to the unpredictable? What is the role of software when its modelling assumptions break down? 9

An illustration – another type of bubble Underwater explosions are used to destroy ships – the initial shock is expected and often not as damaging as the later gas bubble collapse. Left: raw data from sensitive, but un-calibrated pressure gauge Right: calibrated gauge uses averaging to produce smooth curve Use of averaging obscures critical event in this case. 10

Example: wavelet analysis of FX spot prices • Wavelet transforms provide localisation in time and frequency for analysis of financial time series. • This is achieved by scaling and translation of wavelet basis. • Decompose time series, by convolution with dilated and translated mother wavelet, or filter, • Discrete (DWT) Orthogonal Filter pair: H – high pass, G – low pass followed by down-sampling 11

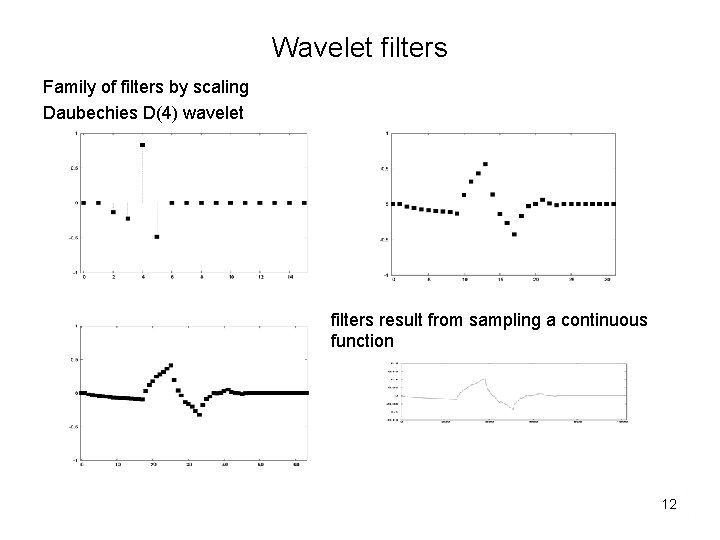
Wavelet filters Family of filters by scaling Daubechies D(4) wavelet filters result from sampling a continuous function 12

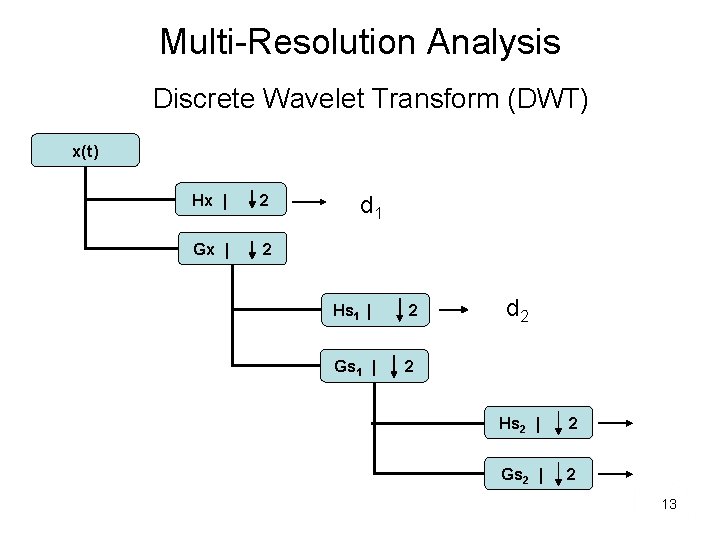
Multi-Resolution Analysis Discrete Wavelet Transform (DWT) x(t) Hx | 2 Gx | 2 d 1 Hs 1 | 2 Gs 1 | 2 d 2 Hs 2 | 2 Gs 2 | 2 13

DWT implementation Orthogonal wavelet transform uses • filters defined by sequences: • satisfying: , , , • This allows for a number of variants in implementation numerical output from different software providers is not identical 14

Discrete Wavelet Transform – Multi-Resolution Analysis For input data , length , produces representation in terms of ‘detail’ and ‘smooth’ wavelet coefficients of length Uses • Data compression – discard coefficients • De-noising Disadvantages • Difficult to relate coefficients to position in original input • Not translation invariant – shifting starting position produces different coefficients 15

Maximal Overlap Wavelet Transform (MODWT) (Stationary Wavelet Transform) • • • Convolution: wavelet filters as in DWT No down-sampling MRA produces N coefficients at each level Requires more storage and computation Not orthonormal Advantages • Translation invariant • Can relate to time scale of original data • Does not require length(x) = 16

Choice of wavelet filter • Short can introduce ‘blocking’ or other features which obscure analysis of data • Long increases number of coefficients affected by ends of data set • Basis Pursuit seeks to optimise choice of wavelet at each level but requires more computation 17

FX: USD, GBP, EUR – NZD 12 noon buying rates, Jan – Jul 2007 18

FX: JPY, USD, GBP, EUR – NZD 12 noon buying rates, Jan – Jul 2007 (from www. x-rates. com) 19

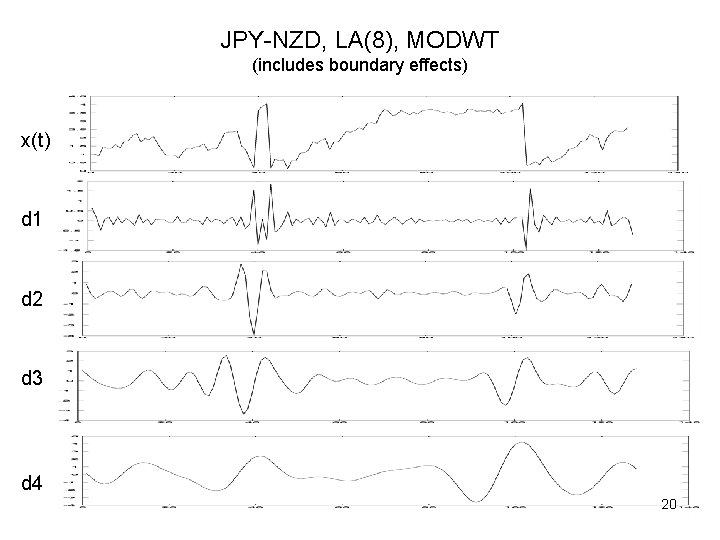
JPY-NZD, LA(8), MODWT (includes boundary effects) x(t) d 1 d 2 d 3 d 4 20

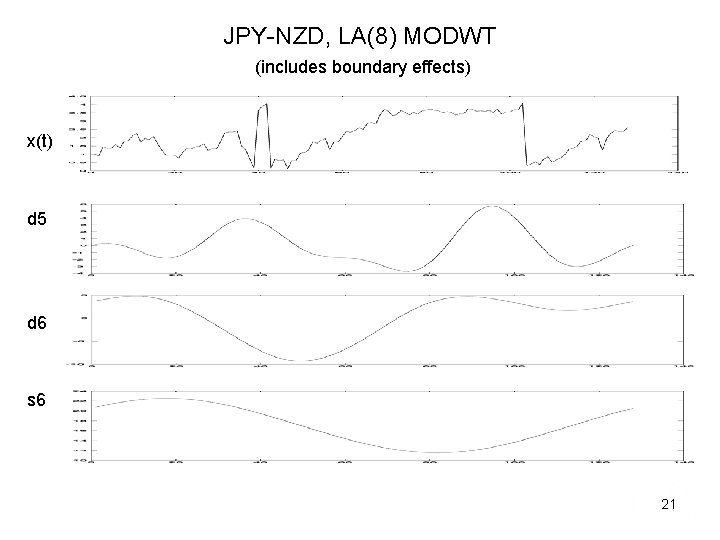
JPY-NZD, LA(8) MODWT (includes boundary effects) x(t) d 5 d 6 s 6 21

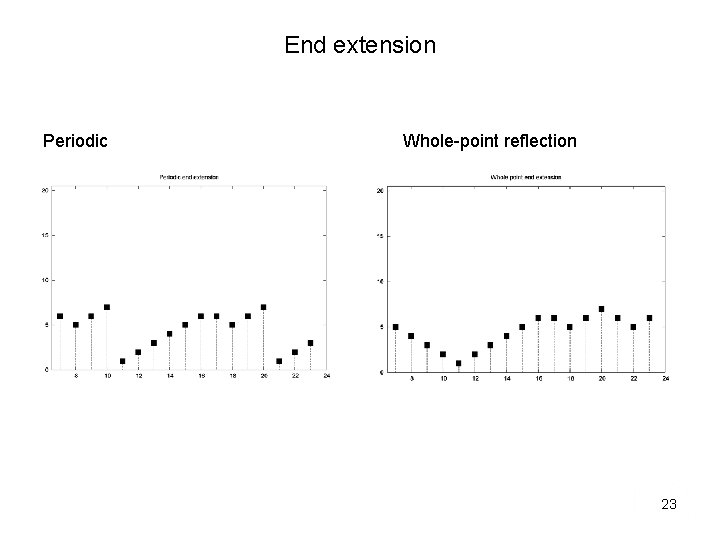
Boundary conditions – end extension • Wavelet transform applies circular convolution to data • What happens at the ends of the data set? • End extension techniques – periodic reflection – whole/half-point pad with zeros • Boundary effects contaminate wavelet coefficients software should indicate where output is influenced by end extension 22

End extension Periodic Whole-point reflection 23

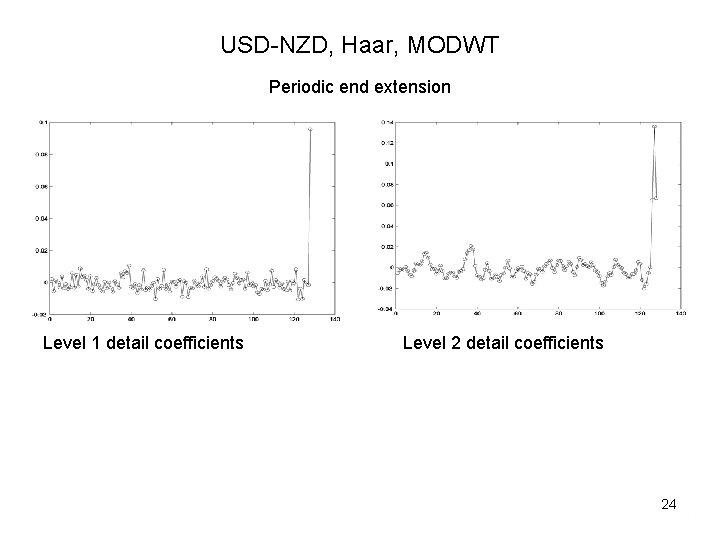
USD-NZD, Haar, MODWT Periodic end extension Level 1 detail coefficients Level 2 detail coefficients 24

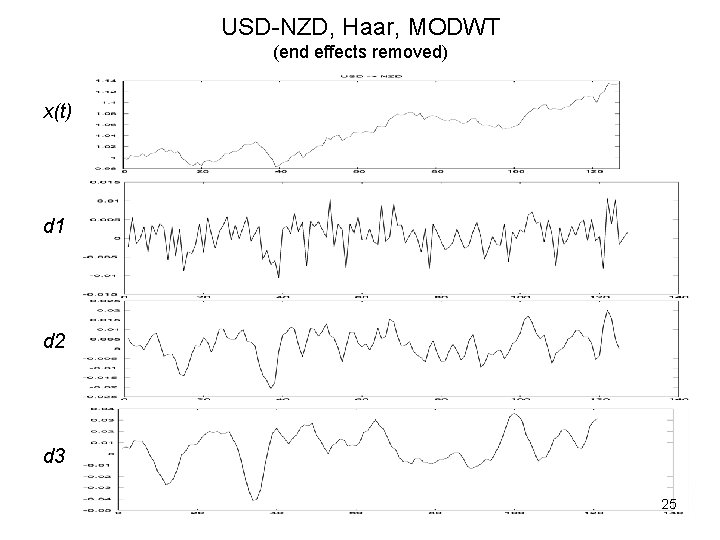
USD-NZD, Haar, MODWT (end effects removed) x(t) d 1 d 2 d 3 25

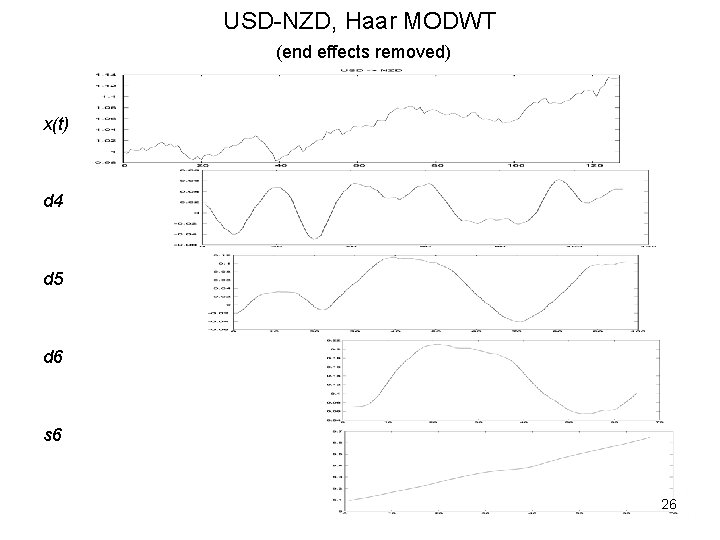
USD-NZD, Haar MODWT (end effects removed) x(t) d 4 d 5 d 6 s 6 26

Wavelet analysis for prediction • Extrapolation from present to near future is useful • Apply wavelet filters to for avoiding boundary effect • Select wavelet scales to identify trend and stochastic parts of data set • Use wavelet coefficients to compute prediction (see Renaud et al. , 2002) 27

Implications for software development • Reproducibility is desirable – algorithms precisely defined to allow independent implementations to produce identical results • Edge effects – contaminate ends of transform for finite signals – software must indicate coefficients affected • Smoothing/averaging – software should indicate when underlying assumptions likely to be invalid • Pre-processing – ensure that structure is not introduced by interpolation to give homogeneous data set 28

Implications for software development • For extreme events – must not obscure or remove data relevant to critical events by averaging, smoothing, filtering. 29