Number Theory and Advanced Cryptography 4 Elliptic Curves

Number Theory and Advanced Cryptography 4. Elliptic Curves Part I: Introduction to Number Theory Part II: Advanced Cryptography Chih-Hung Wang Sept. 2011 1

Elliptic Curve Cryptography o o o Majority of public-key crypto (RSA, D-H) use either integer or polynomial arithmetic with very large numbers/polynomials Imposes a significant load in storing and processing keys and messages An alternative is to use elliptic curves In the mid-1980 s, Miller and Koblitz introduced elliptic curves into cryptography. Offers same security with smaller bit sizes n 4096 -bit key size can be replaced by 313 -bit elliptic curve system 2

Real Elliptic Curves o An elliptic curve is defined by an equation in two variables x & y, with coefficients o Consider a cubic elliptic curve of form n y 2 = x 3 + ax + b n where x, y, a, b are all real numbers n also define zero point O o Have n addition operation for elliptic curve geometrically sum of Q+R is reflection of intersection R 3

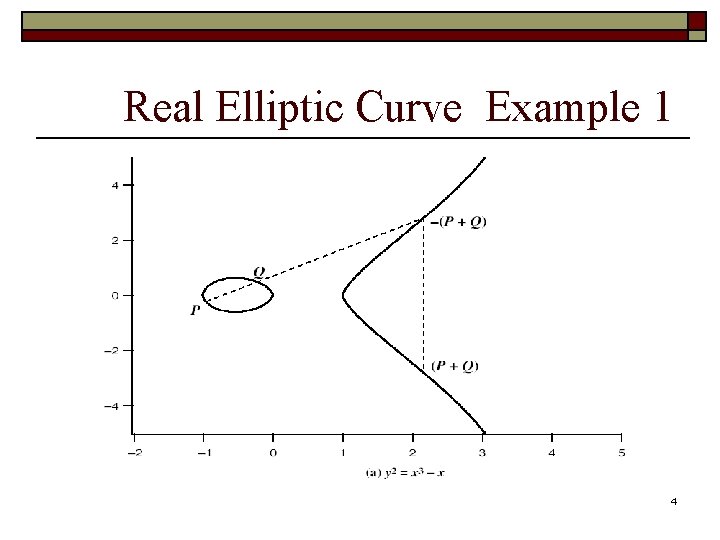
Real Elliptic Curve Example 1 4

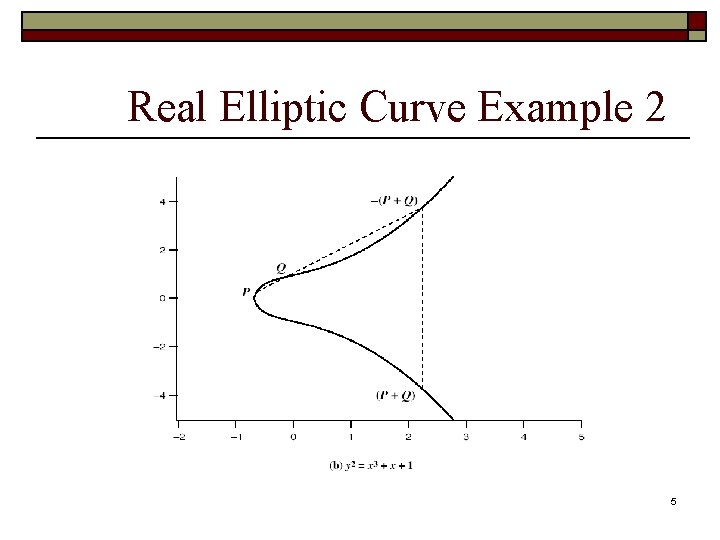
Real Elliptic Curve Example 2 5

Geometric Description of Addition 6

Algebraic Description of Addition P+Q = R =(y. Q-y. P)/(x. Q-x. P) P+P = 2 P = R 7

Addition Law 8

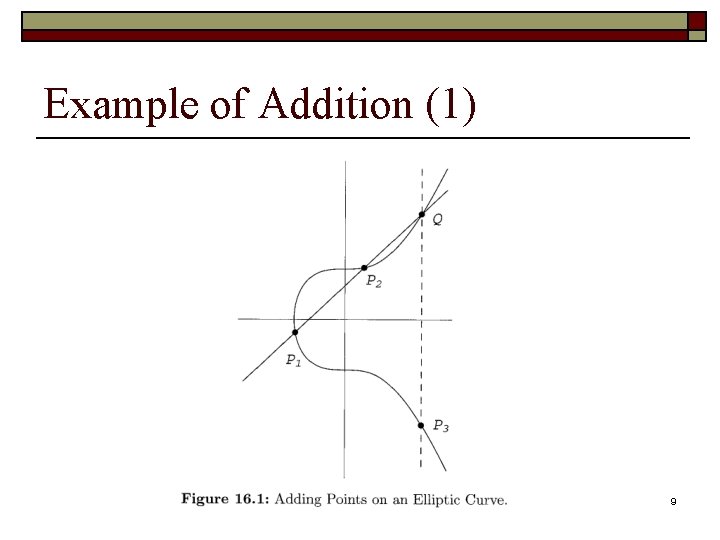
Example of Addition (1) 9

Example of Addition (2) 10

Example of Addition (3) 11

Elliptic Curves Mod p 12

Example 1 13

Example 2 -1 14

Example 2 -2 15

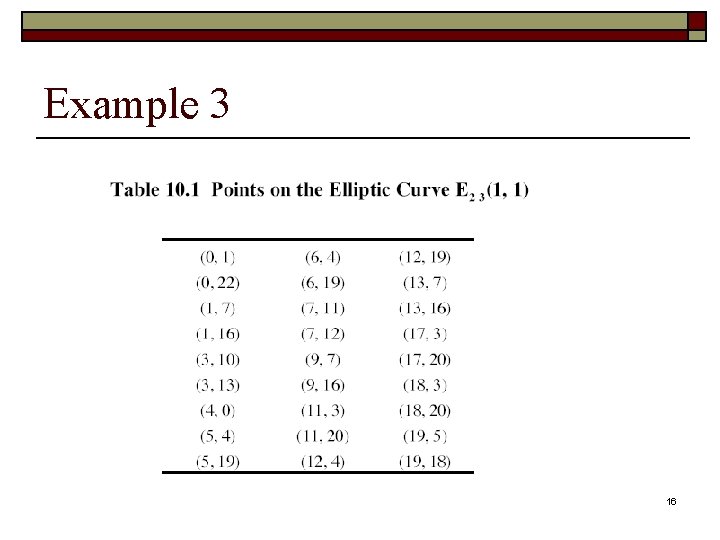
Example 3 16

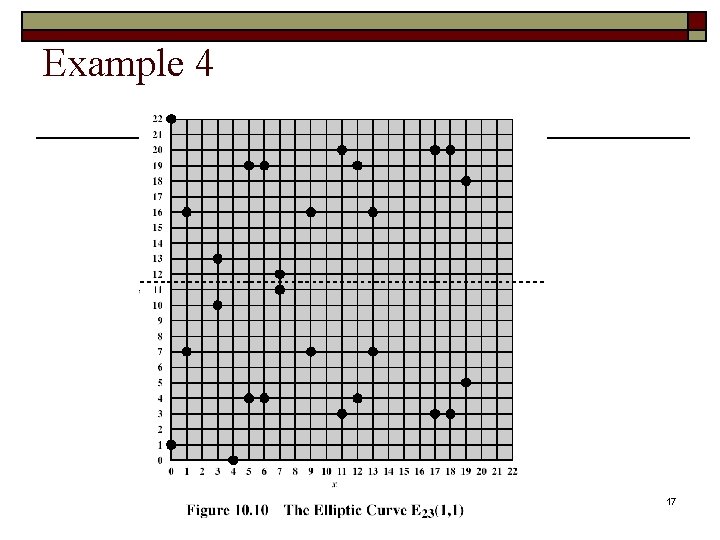
Example 4 17

Law 1 18

Law 2 19

Number of points Mod p 20

Hasse’s Theorem Schoof Algorithm: http: //www. math. rochester. edu/people/grads/jdreibel/ref/12 -7 -05 -Schoof. pdf 21

Discrete Logarithms on EC 22

Representing plaintext (1) 23

Representing plaintext (2) 24

Elliptic Curve Cryptography o ECC addition is analog of modulo multiply o ECC repeated addition is analog of modulo exponentiation o need “hard” problem equiv to discrete log Q=k. P, where Q, P belong to a prime curve n is “easy” to compute Q given k, P n but “hard” to find k given Q, P n known as the elliptic curve logarithm problem n o Certicom example: E 23(9, 17) 25

ECC Diffie-Hellman (1) o can do key exchange analogous to D-H o users select a suitable curve Ep(a, b) o select base point G=(x 1, y 1) with large order n s. t. n. G=O o A & B select private keys n. A<n, n. B<n o compute public keys: PA=n. A×G, PB=n. B×G o compute shared key: K=n. A×PB, K=n. B×PA n same since K=n. A×n. B×G 26

ECC Diffie-Hellman (2) 27

ECC Diffie-Hellman (3) 28

ECC Diffie-Hellman (4) o Page 365 29

ECC Encryption/Decryption (1) o o o o several alternatives, will consider simplest must first encode any message M as a point on the elliptic curve Pm select suitable curve & point G as in D-H each user chooses private key n. A<n and computes public key PA=n. A×G to encrypt Pm : Cm={k. G, Pm+k Pb}, k random decrypt Cm compute: Pm+k. Pb–n. B(k. G) = Pm+k(n. BG)–n. B(k. G) = Pm 30

ECC Encryption/Decryption (2) o Page 363 -364 31

ECC Encryption/Decryption (3) 32

ECC Security (1) o Relies on elliptic curve logarithm problem o Fastest method is “Pollard rho method” o Compared to factoring, can use much smaller key sizes than with RSA etc o For equivalent key lengths computations are roughly equivalent o Hence for similar security ECC offers significant computational advantages 33

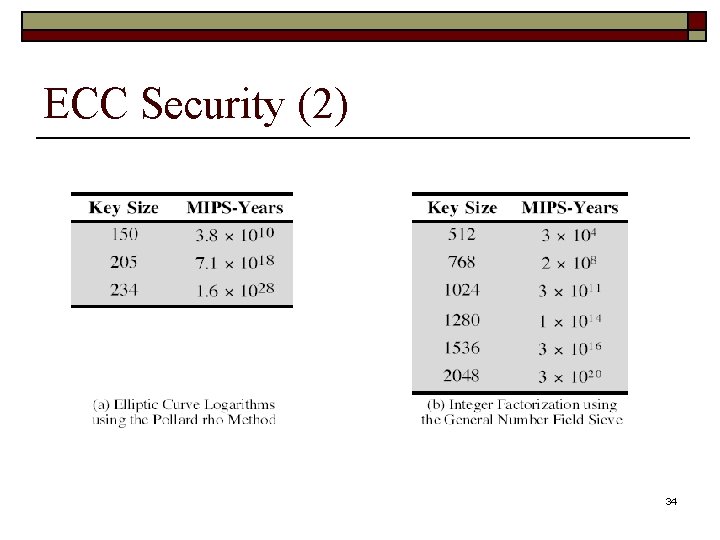
ECC Security (2) 34

ECC Digital Signature (page 365366) Signing 35

ECC Digital Signature (page 365366)II Verification 36

ECC Digital Signature (1) 37

ECC Digital Signature (2) 38

ECC Digital Signature (3) 39