Number Systems Part 2 Numerical Overflow Right and

Number Systems Part 2 Numerical Overflow Right and Left Shifts Storage Methods Subtraction Ranges

Numerical Overflow �An overflow is when something doesn’t fit in a certain space �Numeric overflow is when the storage for a calculation is too small to hold the result �For example we have an 8 bits register, if we add two binary numbers and the result turns out to be 9 bits it would not fit in the register

Example �Let’s �Add say we have an 8 bit register the following; 1111+ 1010 �Do we have an overflow?

Numerical Overflow �When we have a numeric overflow we will have an error in our calculation �When we have an overflow we would need to remove the extra bit at the start of the number �Lets say we had a 7 bit register and the result of a calculation is 1100 the actual answer would be 1001100

Example �Let’s �Add say we have a 7 bit register the following; 1101111+ 1101101 �Do we have an overflow? �Actual answer =

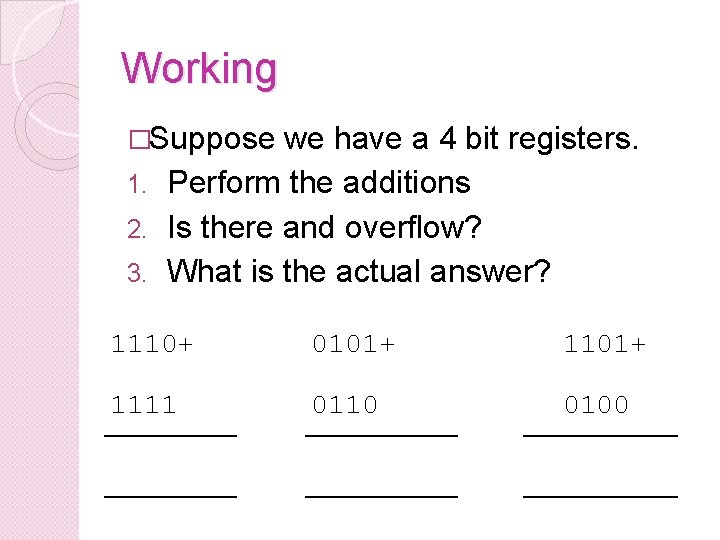
Working �Suppose we have a 4 bit registers. 1. Perform the additions 2. Is there and overflow? 3. What is the actual answer? 1110+ 0101+ 1111 0110 0100

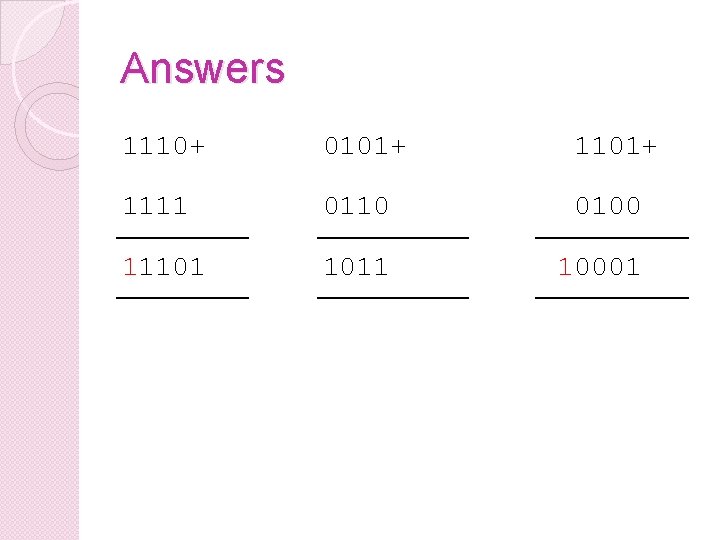
Answers 1110+ 0101+ 1111 0110 0100 11101 1011 10001

What is Bit Shifting? �Bit shifting is the process of moving all the bits in a binary number �We have two shifts 1. A right shift 2. A left shift � The right shift would divide the number while the left would multiply it

Right Shift �The right shift is used to perform divisions �Hence if we where to perform three right shifts we would be diving the number by 2 three times �For example if we shift 101100112, = 17910 right by three places, we get 000101102 = 2210 � 179 /2 = 89 � 90/2 = 44 � 45/2 = 22

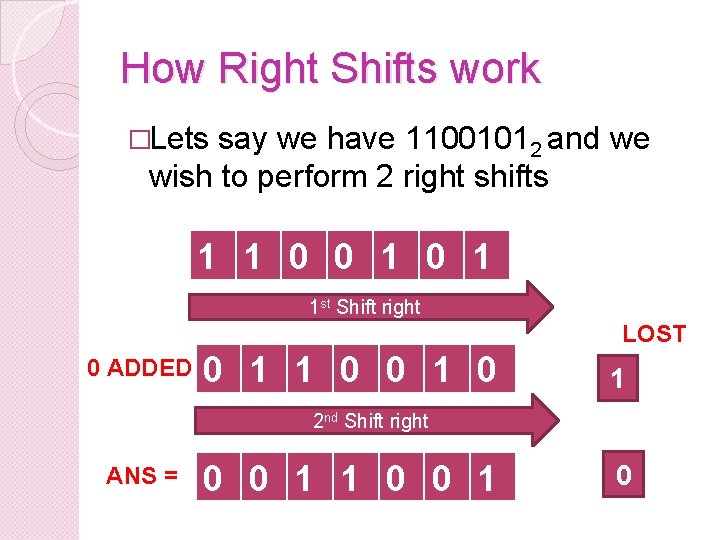
How Right Shifts work �Lets say we have 11001012 and we wish to perform 2 right shifts 1 1 0 0 1 1 st Shift right LOST 0 ADDED 0 1 1 0 0 1 2 nd Shift right ANS = 0 0 1 1 0 0 1 0

Working �Shift the numbers to the right by the number of shifts indicated in the brackets; 1. 2. 3. 4. 5. 1000110 (2) 1110001 (4) 1111000 (1) 0101 (4) 0000111 (3) Change to decimal to check your answers

1000110 70 1110001 113 1111000 120 0100011 35 0111000 56 0010001 17 0011100 28 0111100 60 0001110 14 0000111 7 0101 85 0000111 7 00101010 42 0000011 3 00010101 21 0000001 1 00001010 10 0000000 0 00000101 5

Left Shift �The left shift is used to perform multiplications �Hence if we where to perform four left shifts we would be multiplying the number by 2 four times �If any bits are lost when shifting left the result is no longer accurate �For example if we shift 011001012, = 10110 left by one place, we get 110010102 = 20210

How Left Shifts work �Lets say we have 011001012 and we wish to perform 2 left shifts 0 1 1 0 0 1 LOST 0 1 st Left Shift 1 1 0 0 1 0 2 nd Left Shift 1 1 0 0 Answer no longer correct as a 1 was lost

Working �Shift the numbers to the left by the number of shifts indicated in the brackets, also state which answers are not correct. 1. 2. 3. 4. 5. 0000110 (4) 1110001 (3) 0011110 (1) 0101 (2) 0000111 (3) Change correct answers to decimal to check your answers

0000110 6 1110001 0011110 30 0001100 12 1100010 0111100 60 0011000 24 1000100 0110000 48 0001000 1100000 96 Not correct 0101 0000111 7 1010 0001110 14 01010100 0011100 28 Not Correct 0111000 56

Storage Methods �When we have a fixed register we might want to store out binary number in a certain way �The three ways are using; 1. sign and magnitude (first digit is 0 = positive, first digit is 1 = negative) 2. one’s complement 3. two’s complement.

Example 1 �Lets say we have a register of 8 -bits and we wish to store the number 1410 �Since the number is positive, all we need to do is convert it to binary and store it �It would be the same in the three different storage methods, 1410 = 000011102

Example 2 �Lets say I have an 8 bit register and want to store -1410 �The number now changes since it is negative, we first change it to binary = 000011102 Sign and Magnitude 10001110 Note that the fist digit is 1 because in this case 14 is a negative number. One’s Complement 11110001 In this case we simply applied NOT on the binary value of 14. Two’s Complement 11110010 We change the binary number 14 into two’s complement

Working �Convert the following to; a) Sign and magnitude b) One’s Complement c) Two’s Complement Size of register is indicated in the brackets. 1. 3310 (8) 2. -6010 (9) 3. -4410 (7) 4. 1010 (5) 5. -7410 (10)

Subtraction �We are able to subtract using binary numbers thanks to Two’s Complement �When we need to subtract in binary we first need to change the negative number to Two’s Complement �if we have 22 – 10 we have to change 10 to Two’s Complement then perform an addition �Binary numbers must be of the same length in order to subtract in binary

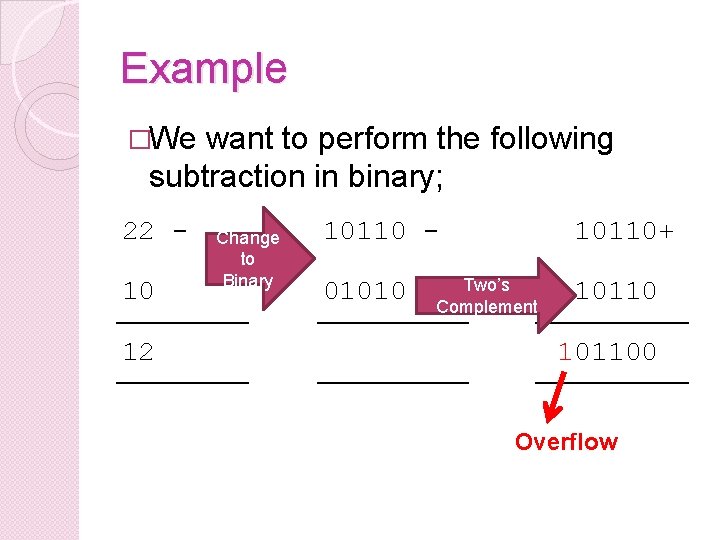
Example �We want to perform the following subtraction in binary; 22 10 12 Change to Binary 10110 01010 10110+ Two’s Complement 101100 Overflow

Working �Perform the following subtractions in binary; 1. 2. 3. 4. 5. 30 -20 100 – 50 50 – 25 5– 2 66 - 60

Ranges �A ranges determines the lowest and the highest values which can be represented by a certain register �We will be going through two types of ranges using binary; 1. normal binary 2. two’s complement.

Normal Binary �What is the range of numbers which can be represented using 8 -bits? �Since we have 8 Bits, the maximum value represented in binary is 1111 and the smallest is 0000. �If we convert these numbers to decimal we end up with: 0 to 255

Example �What is the range of numbers which can be represented using 5 -bits? �Since we have 5 Bits, the maximum value represented in binary is 11111 and the smallest is 00000. �If we convert these numbers to decimal we end up with: 0 to 31

Two’s Complement �What is the range of numbers which can be represented using 8 -bits in two’s complement? �The first number in two’s complement identifies the number as a negative number, the highest possible positive number is 011111112 = 12710 �To find the smallest number we convert the positive number to negative so in this case -12710.

Example �What is the range of numbers which can be represented using 10 -bits in two’s complement? � 0111112 = 51110 � 51110 becomes negative to show the smallest number helps = -51110. �The range is: -511 to 510