Number Systems and Binary Arithmetic Introduction to Numbering

Number Systems and Binary Arithmetic

Introduction to Numbering Systems n We are all familiar with the decimal number system (Base 10). Some other number systems that we will work with are: – Binary Base 2 – Octal Base 8 – Hexadecimal Base 16

Characteristics of Numbering Systems 1) 2) 3) 4) 5) 6) The digits are consecutive. The number of digits is equal to the size of the base. Zero is always the first digit. The base number is never a digit. When 1 is added to the largest digit, a sum of zero and a carry of one results. Numeric values determined by the have implicit positional values of the digits.

Significant Digits Binary: 11101101 Most significant digit Least significant digit Hexadecimal: 1 D 63 A 7 A Most significant digit Least significant digit

Binary Number System Also called the “Base 2 system” n The binary number system is used to model the series of electrical signals computers use to represent information n 0 represents the no voltage or an off state n 1 represents the presence of voltage or an on state n

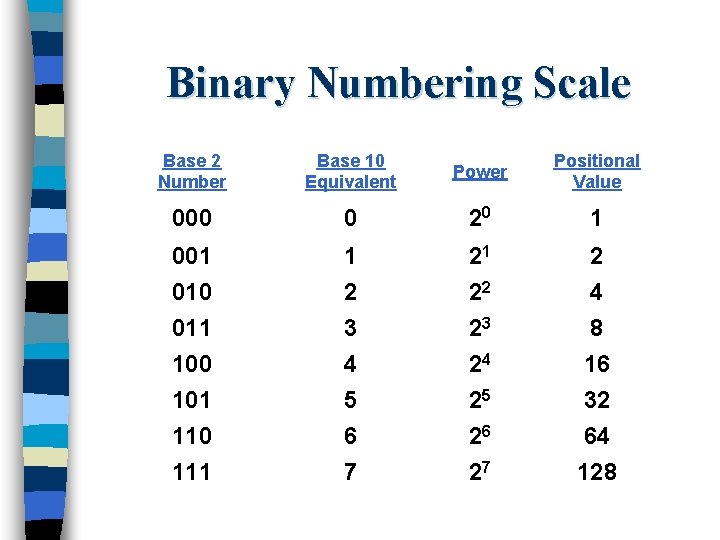
Binary Numbering Scale Base 2 Number Base 10 Equivalent Power Positional Value 000 0 20 1 001 010 011 100 101 110 111 1 2 3 4 5 6 7 21 22 23 24 25 26 27 2 4 8 16 32 64 128

Binary Addition 4 Possible Binary Addition Combinations: (1) Carry (3) 0 +0 00 1 +0 01 (2) Sum (4) 0 +1 01 1 +1 10 Note that leading zeroes are frequently dropped.

Decimal to Binary Conversion The easiest way to convert a decimal number to its binary equivalent is to use the Division Algorithm n This method repeatedly divides a decimal number by 2 and records the quotient and remainder n – The remainder digits (a sequence of zeros and ones) form the binary equivalent in least significant to most significant digit sequence

Division Algorithm Convert 67 to its binary equivalent: 6710 = x 2 Step 1: 67 / 2 = 33 R 1 Step 2: 33 / 2 = 16 R 1 Step 3: 16 / 2 = 8 R 0 Step 4: 8 / 2 = 4 R 0 Step 5: 4 / 2 = 2 R 0 Step 6: 2 / 2 = 1 R 0 Step 7: 1 / 2 = 0 R 1 Divide 67 by 2. Record quotient in next row Again divide by 2; record quotient in next row Repeat again STOP when quotient equals 0 1 0 0 1 12

Binary to Decimal Conversion n The easiest method for converting a binary number to its decimal equivalent is to use the Multiplication Algorithm n Multiply the binary digits by increasing powers of two, starting from the right n Then, to find the decimal number equivalent, sum those products

Multiplication Algorithm Convert (10101101)2 to its decimal equivalent: Binary 1 0 1 Positional Values 27 26 25 24 23 22 21 20 Products x x x x 128 + 32 + 8 + 4 + 1 17310

Octal Number System n Also known as the Base 8 System n Uses digits 0 - 7 n Readily converts to binary n Groups of three (binary) digits can be used to represent each octal digit n Also uses multiplication and division algorithms for conversion to and from base 10

Decimal to Octal Conversion Convert 42710 to its octal equivalent: 427 / 8 = 53 R 3 53 / 8 = 6 R 5 6 / 8 = 0 R 6 Divide by 8; R is LSD Divide Q by 8; R is next digit Repeat until Q = 0 6538

Octal to Decimal Conversion Convert 6538 to its decimal equivalent: Octal Digits Positional Values Products 6 5 82 81 x x 3 80 384 + 40 + 3 42710 x

Octal to Binary Conversion Each octal number converts to 3 binary digits To convert 6538 to binary, just substitute code: 6 5 3 110 101 011

Hexadecimal Number System n Base 16 system n Uses digits 0 -9 & letters A, B, C, D, E, F n Groups of four bits represent each base 16 digit

Decimal to Hexadecimal Conversion Convert 83010 to its hexadecimal equivalent: 830 / 16 = 51 R 14 51 / 16 = 3 R 3 3 / 16 = 0 R 3 = E in Hex 33 E 16

Hexadecimal to Decimal Conversion Convert 3 B 4 F 16 to its decimal equivalent: Hex Digits Positional Values Products 3 x B x 4 x F x 163 162 161 160 12288 +2816 + 64 +15 15, 18310

Binary to Hexadecimal Conversion The easiest method for converting binary to hexadecimal is to use a substitution code n Each hex number converts to 4 binary digits n

Substitution Code Convert 010101110011010102 to hex using the 4 -bit substitution code : 5 A 6 A E 6 0101 0110 1010 1110 0110 1010 56 AE 6 A 16

Substitution Code Substitution code can also be used to convert binary to octal by using 3 -bit groupings: 2 5 5 2 7 1 5 2 010 101 010 111 001 101 010 255271528

Complementary Arithmetic n 1’s complement – Switch all 0’s to 1’s and 1’s to 0’s Binary # 1’s complement 10110011 01001100

Complementary Arithmetic n 2’s complement – Step 1: Find 1’s complement of the number Binary # 11000110 1’s complement 00111001 – Step 2: Add 1 to the 1’s complement 00111001 + 00000001 00111010

Signed Magnitude Numbers 110010. . Sign bit 0 = positive 1 = negative … 00101110010101 31 bits for magnitude This is your basic Integer format

Floating Point Numbers n Real numbers must be normalized using scientific notation: 0. 1…× 2 n where n is an integer n Note that the whole number part is always 0 and the most significant digit of the fraction is a 1 – ALWAYS!

Floating Point Operations n Before two floating point numbers can be added, the exponents for both numbers must be made equal – hence the term “floating point” n NIST Standard Format (32 -bit word) ± 8 -bit exponent 23 -bit fraction field

Bias Notation n The exponent field (8 bits) can be used to represent integers from 0 -255 n Because of the need for negative exponents to be represented as well, the range is offset or biased from – 128 to + 127 n In this way, both very large and very small numbers can be represented

Double Precision n Double word format that increases both the length of the fraction (precision) but also the size of the bias (magnitude) n NIST ± Standard format (64 bits) 10 -bit exponent 53 -bit fraction field

Error Considerations n The “Hole at Zero” Problem – Regardless of how large an exponent field is, there are still smaller positive and negative numbers about zero that cannot be represented – In bias notation, +2 -129 and - 2 -129 are beyond the acceptable range – The “Hole at Zero” defines the range of values near zero that cannot be stored

Computational Errors When converting base 10 fractions to binary, only those fractions whose values can be expressed as a sum of base 2 fractions will convert evenly n All other base 10 fractions feature a least significant bit that is either rounded or truncated – an approximation n When two such numbers are multiplied, the rounding error is compounded n