Number Rational Numbers Indices Rational Numbers By the

Number: Rational Numbers & Indices Rational Numbers By the end of this lesson you will be able to explain and calculate the following: 1. A Rational Number 2. An Irrational Number 3. Order of Operations

Real Numbers �We use numbers such as integers, fractions and decimals every day. �They form part of what is called the Real Number System. �Real numbers can be divided into two categories rational numbers and irrational numbers

The set of real numbers, R �The set of real numbers is a collection that contains natural, integer, rational and irrational numbers. �Let us first define each of these sets and see their relationship to each other.

Order of operations using integers �Anton has calculated the answer to 5 + 6 × 4 as 44 �Marco insists that the answer is 29. �Who is correct? �The order of operations requires that: 1. 2. 3. all expressions in brackets are evaluated first, beginning with the innermost pair of brackets then, all multiplication and division are evaluated, working from left to right and finally, any addition and subtraction, working from left to right.

Worked Example

Worked Example


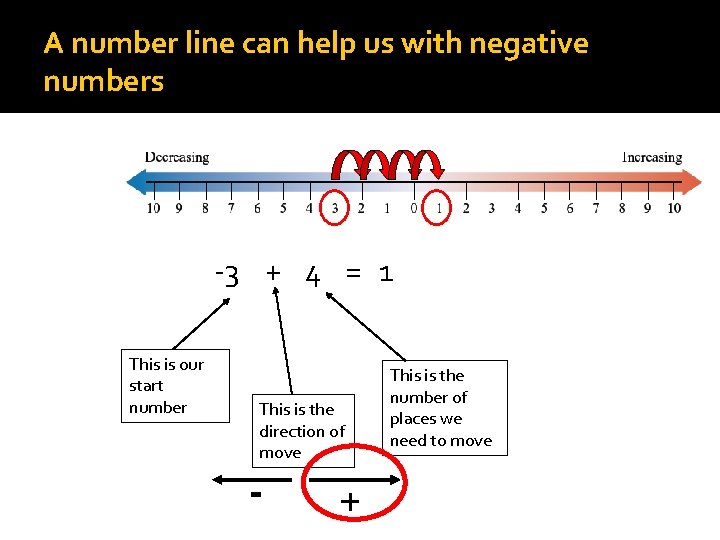
A number line can help us with negative numbers -3 + 4 = 1 This is our start number This is the direction of move - + This is the number of places we need to move
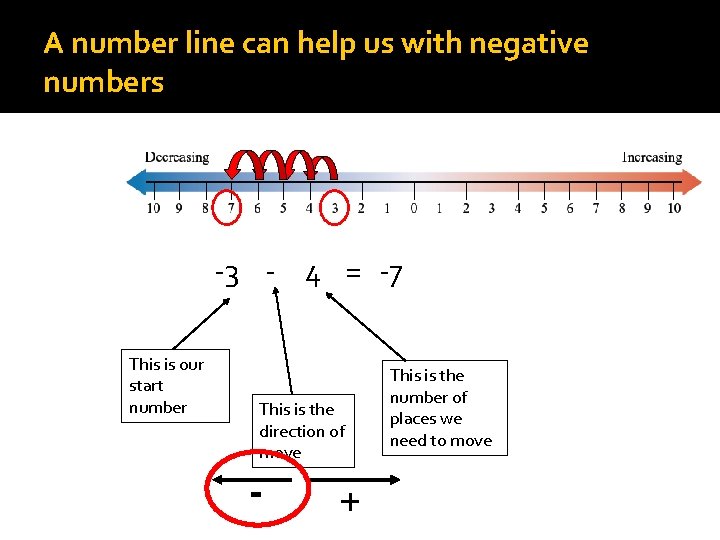
A number line can help us with negative numbers -3 - 4 = -7 This is our start number This is the direction of move - + This is the number of places we need to move
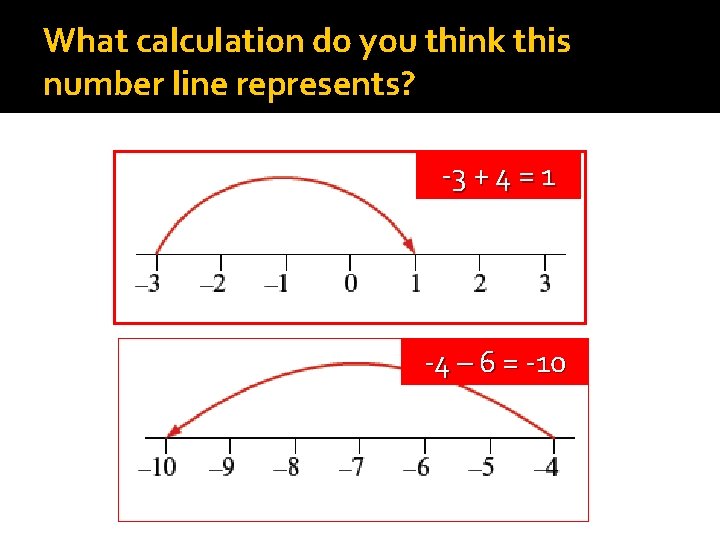
What calculation do you think this number line represents? -3 + 4 = 1 -4 – 6 = -10

Now. …there is one more thing we need to know. Remembering AIS and SID can help us with this next stage. AIS and SID

AIS = Add If Same Look at the signs in the middle, if they are the same, then replace them with +. + 8 - - 6 = 14
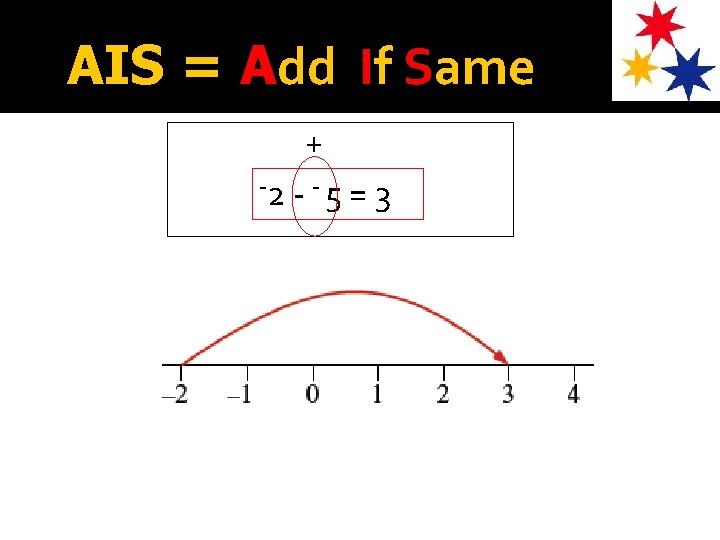
AIS = Add If Same + -2 - - 5 = 3

SID = Subtract If Different Look at the signs in the middle, if they are different, then replace them with -. - 8 + - 6 =2

SID = Subtract If Different - 4 + 6 = 10 - -

But what about this one? Can you use all your knowledge of negative numbers so far to find the answer to these calculations? -6 -6 + 2= + - 8= -8 2 Remember: This is your start number and the new sign in the middle is the direction

Multiplying / Dividing �When multiplying integers, the following rules are obeyed. a) b) c) d) Positive × Positive = Positive × Negative = Negative × Positive = Negative × Negative = Positive 5 × 8 = 40 5 × − 8 = − 40 − 5 × − 8 = 40 �When dividing integers, use the same rules a) Positive ÷ Positive = Positive 16 ÷ 2 = 8 b) Positive ÷ Negative = Negative 16 ÷ − 2 = − 8 c) Negative ÷ Positive = Negative − 16 ÷ 2 = − 8 d) Negative ÷ Negative = Positive − 16 ÷ − 2 = 8

Multiplying / Dividing �When multiplying and dividing integers: like signs give positive answers, unlike signs give negative answers.



Homework Answers
- Slides: 22