Nuffield FreeStanding Mathematics Activity Refurbishing a room Nuffield

Nuffield Free-Standing Mathematics Activity Refurbishing a room © Nuffield Foundation 2011

Refurbishing a room Where shall I start? What order shall I do things in? How soon can it be ready? ’ You can answer such questions by using critical path analysis. This activity will show you how to do this.

Critical Path Analysis The techniques of critical path analysis were developed in the late 1950 s by two American companies, Dupont and Remington Rand. They were used to plan large-scale projects such as the development of the Polaris Missile. The algorithm determines the minimum time for a project to be completed and optimises manpower and resources to achieve this minimum completion time.

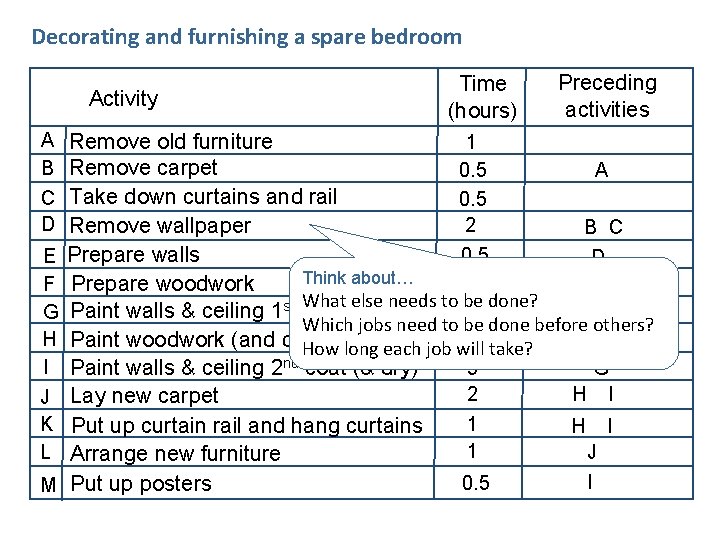
Decorating and furnishing a spare bedroom Activity A B C D E F G H I J K L M Time (hours) Preceding activities Remove old furniture 1 Remove carpet 0. 5 A Take down curtains and rail 0. 5 2 Remove wallpaper B C 0. 5 Prepare walls D Think about… D 1. 5 Prepare woodwork What else needs to be done? Paint walls & ceiling 1 st coat (& dry) E 5 Which jobs need to be done before others? 8 take? F Paint woodwork (and dry) How long each job will 5 G Paint walls & ceiling 2 nd coat (& dry) 2 H I Lay new carpet 1 Put up curtain rail and hang curtains H I 1 J Arrange new furniture I 0. 5 Put up posters

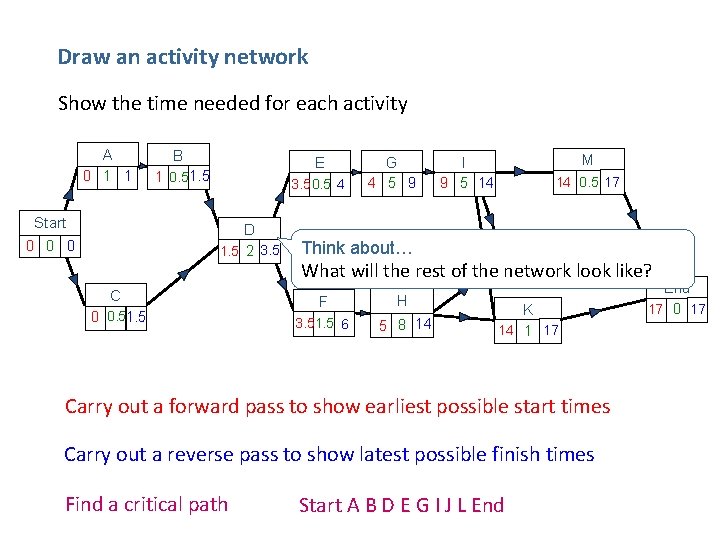
Draw an activity network Show the time needed for each activity A 0 1 1 Start B E 1 0. 5 1. 5 3. 5 0. 5 4 D 1. 5 2 3. 5 0 0 0 C 0 0. 51. 5 G 4 5 9 Think about… What will the rest of F H 3. 51. 5 6 5 8 14 M I 9 5 14 14 0. 5 17 L J 17 2 16 16 the 14 network look 1 like? K 14 1 17 Carry out a forward pass to show earliest possible start times Carry out a reverse pass to show latest possible finish times Find a critical path Start A B D E G I J L End 17 0 17

Critical path analysis Step 1 List the activities with a time estimate for each. Step 2 Note which activities must precede others. Step 3 Draw an activity network, including the time for each activity. Step 4 Carry out a forward pass to find the earliest possible start times. Step 5 Carry out a reverse pass to find the latest possible finish times. Step 6 Identify critical activities and find a critical path.

Critical activities must start on time if the project is not to be delayed. They are those for which: Latest finish time = earliest start time + duration A Furniture removal must start at 0 hours B Carpet removal must start at 1 hours D Wallpaper removal must start at 1. 5 hours E Wall preparation must start at 3. 5 hours G 1 st coat on walls must start at 4 hours I 2 nd coat on walls must start at 9 hours J Carpet laying must start at 14 hours L Arranging new furniture must start at 16 hours Think about… What comes next?

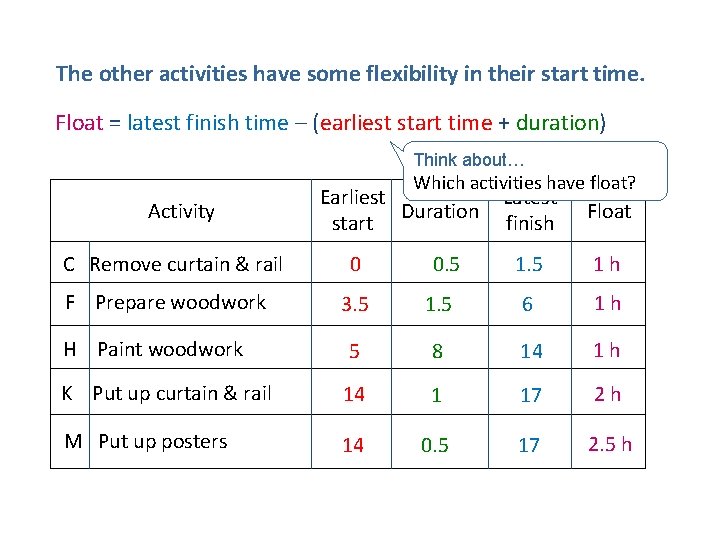
The other activities have some flexibility in their start time. Float = latest finish time – (earliest start time + duration) Think about… Which activities have float? Activity C Remove curtain & rail F Prepare woodwork Earliest Duration start 0 0. 5 Latest finish Float 1. 5 1 h 3. 5 1. 5 6 1 h H Paint woodwork 5 8 14 1 h K Put up curtain & rail 14 1 17 2 h M Put up posters 14 0. 5 17 2. 5 h

Refurbishing a room Reflect on your work • Summarise the steps in working out a critical path. • Describe what is meant by ‘float’. • What effect will the number of helpers involved have on the minimum completion time? • When on your finished network will there be the need for at least one helper to allow some of the activities to take place simultaneously? • What practical considerations need to be taken into account when working out the minimum completion time?