Nuclear tensor forces and a signal for scalechiral

Nuclear tensor forces and a signal for scale-chiral symmetry in nuclei What I would propose to work out at RAON Mannque Rho CEA Saclay 2 nd APCTP-ECT* Workshop 2015

Monday’s talk: talk a) Start with scale-invariant hidden local symmetry with dilaton s and pions p coupled to matter fields r and w subject to explicit symmetry breaking away from the IR fixed point and current quark masses. The degrees of freedom are the nucleons (N), the hidden gauge mesons r & w and a multiplet of p. NG s and p‘s. b) The effective Lagrangian is matched via correlators to QCD at the matching scale LM from which the EFT picks up IDD (intrinsic density dependence) from QCD condensates. c) Nuclear dynamics is described by “double decimation” RG flows from LM, the first decimation leading to Vlowk endowed with IDD and the second to what corresponds to Fermi-liquid fixed point approach to many body problem. d) Monday’s talk was focused on dense matter, n > n 0.

This talk I will focus on processes near nuclear matter, in particular connected to nuclear tensor forces. I will then propose how to “see” the manifestation – i. e. , a signal – of scale-chiral symmetry of QCD in nuclear medium. Perhaps in RAON-type physics!(? ) Debate between Gerry Brown and Steven Weinberg in early 1990’s.

To go from soft-pion scale up to higher scale Ø At E ≈ 0 , Soft pion/current algebra applies: Write Ø Notice An Invariance: This is a “redundancy” , exploit it to gauge the symmetry to “hidden local symmetry (HLS)” à la Harada and Yamawaki. Provides potentially powerful tool to go toward the vector meson scale.

Brown-Weinberg debate On EFT in nuclear physics Brown (espousing HLS): “the r meson is essential in nuclear physics”. Weinberg (espousing standard p. Ch. PT): “the r is not needed, its effect can be incorporated in counter terms involving pions only” Weinberg’s “mended symmetry” acknowledges Brown’s thesis

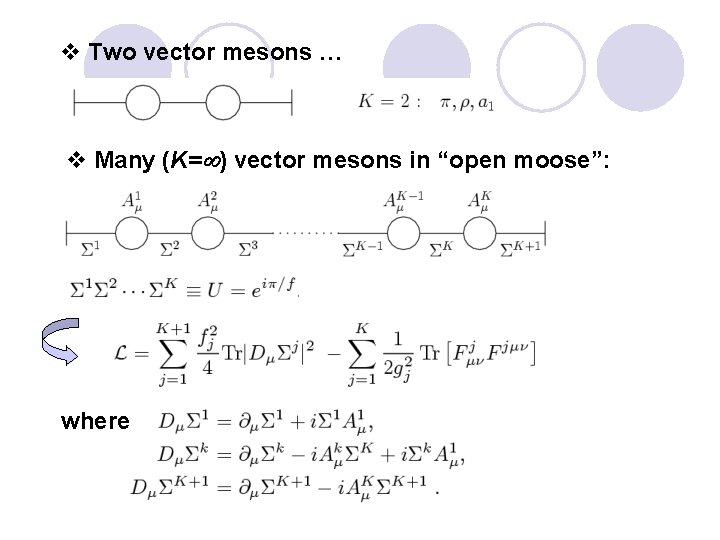
Something deep about HLS is involved in the debate Approaching QCD with effective fields involves Infinite towers of vector mesons as hidden gauge fields Moose construction by Georgi et al. 1999 v One vector meson:

v Two vector mesons … v Many (K= ) vector mesons in “open moose”: where

And take continuum limit with K = , e→ 0 : → 5 D YM o Chiral symmetry in 4 D is elevated to a local gauge symmetry in 5 D. It also comes from string theory, e. g. , Sakai and Sugimoto 2003. So at some mass scale, vector mesons must appear. But the question is: Is any of them essential in nuclear physics? The answer is most likely YES.

Tensor forces: An old problem with a new twist

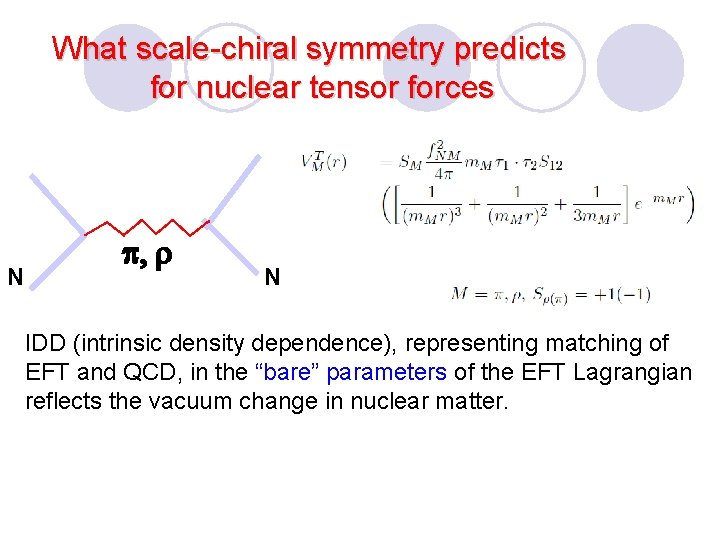
What scale-chiral symmetry predicts for nuclear tensor forces N p, r N IDD (intrinsic density dependence), representing matching of EFT and QCD, in the “bare” parameters of the EFT Lagrangian reflects the vacuum change in nuclear matter.

Crucial ingredient: chiral symmetry locked to scale symmetry Crewther and Tunstall 2013 At a. IR, in the chiral limit , m Dm =qmm = m Am = 0. s (“dialon”) and p (pseudo) NG bosons fp <c> = fs Dilaton condensate provides IDD’s to EFT Lagrangian

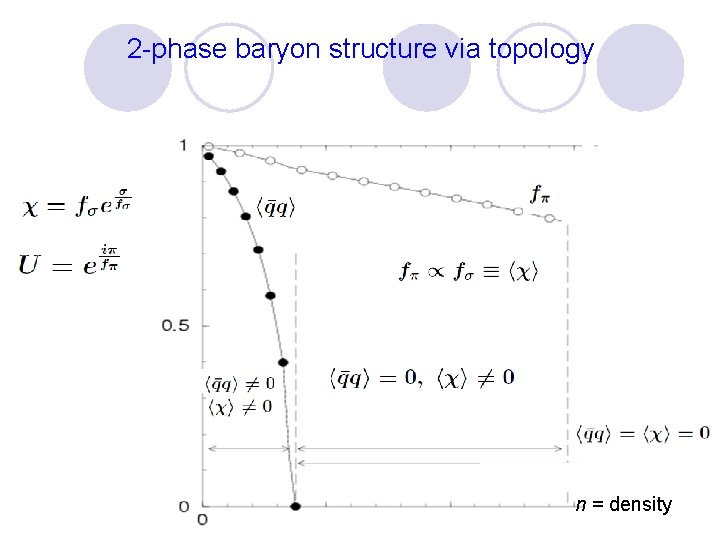
2 -phase baryon structure via topology n = density

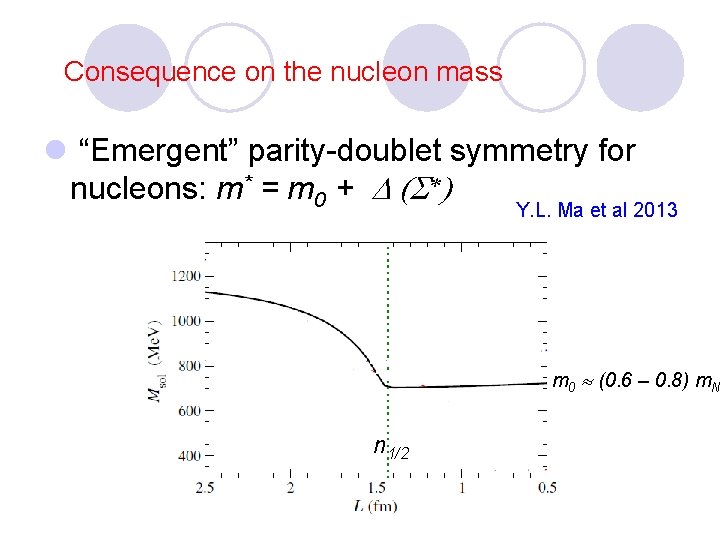
Consequence on the nucleon mass l “Emergent” parity-doublet symmetry for nucleons: m* = m 0 + D (S*) Y. L. Ma et al 2013 m 0 (0. 6 – 0. 8) m. N n 1/2

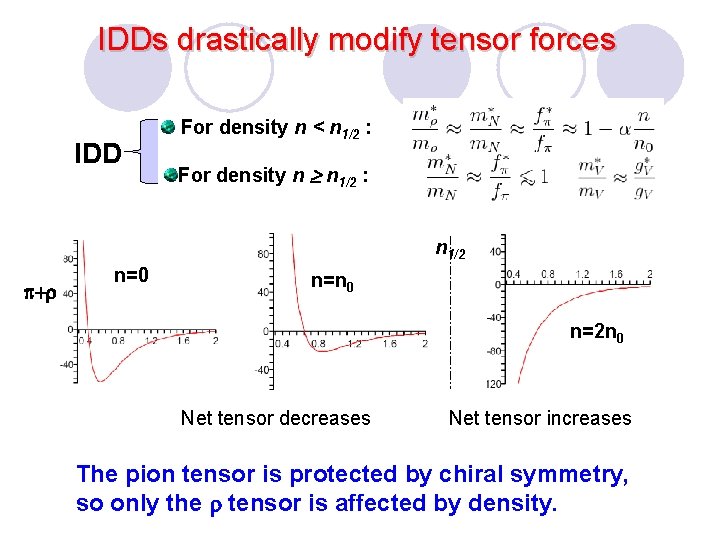
IDDs drastically modify tensor forces IDD For density n < n 1/2 : For density n n 1/2 : n 1/2 p+r n=0 n=n 0 n=2 n 0 Net tensor decreases Net tensor increases The pion tensor is protected by chiral symmetry, so only the r tensor is affected by density.

Impact on Eo. S For matter with excess of neutrons (i. e. , neutron star) the “symmetry energy” Esym plays a dominant role.

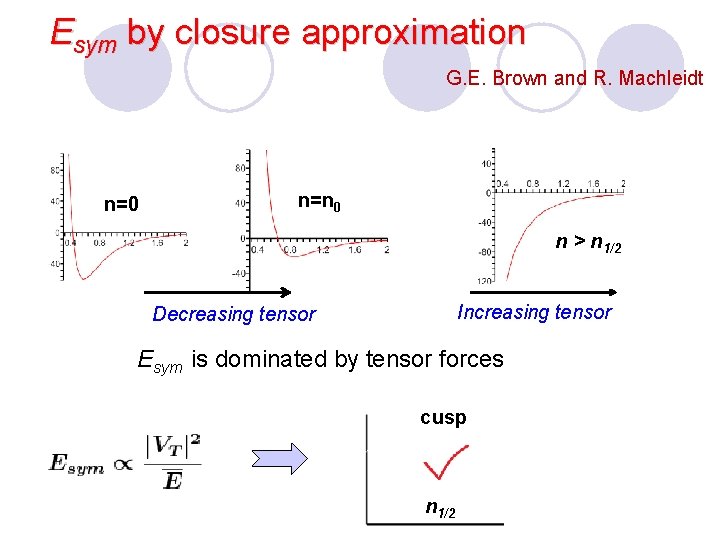
Esym by closure approximation G. E. Brown and R. Machleidt n=0 n=n 0 n > n 1/2 Increasing tensor Decreasing tensor Esym is dominated by tensor forces cusp n 1/2

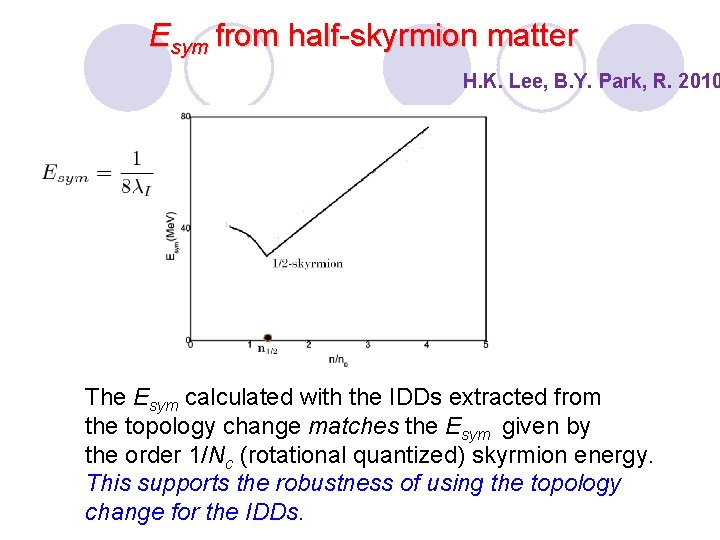
Esym from half-skyrmion matter H. K. Lee, B. Y. Park, R. 2010 The Esym calculated with the IDDs extracted from the topology change matches the Esym given by the order 1/Nc (rotational quantized) skyrmion energy. This supports the robustness of using the topology change for the IDDs.

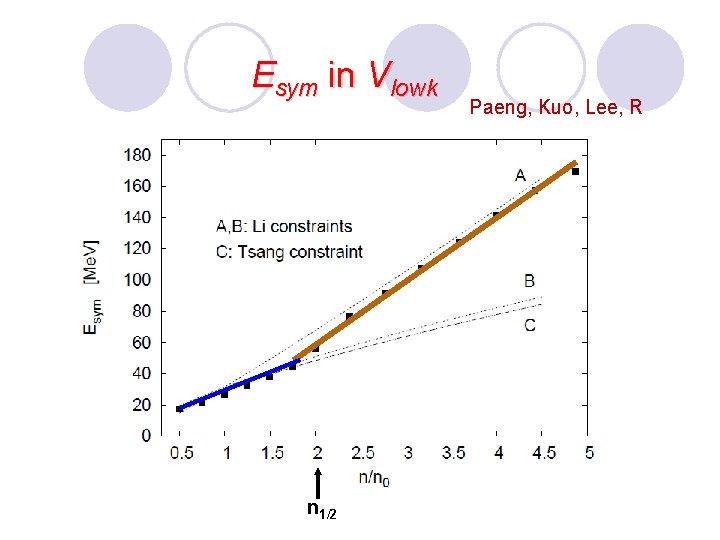
Esym in Vlowk n 1/2 Paeng, Kuo, Lee, R

Surprising things happen in Finite nuclei and nuclear matter

Use “Double decimation” Bogner, Kuo et al, ar. Xiv: nucl-th/0305035 There are roughly two RG decimations in nuclear many-body EFT a) Decimate from Lc to ~ (2 -3) fm-1 or ~ 400 Me. V up to which accurate NN scattering data are available say, Elab ≤ 350 Me. V. Call it Ldata. Yields Vlow. K b) Decimate from Ldata to Fermi surface scale LFS using Vlow. K operative up to Elab. This derives Fermi liquid fixed point theory valid for nuclear matter. Fluctuate around Fermi surface; Many body technique

Vlowk - RG approach Kuo, Brown, Holt, Schwenk et al

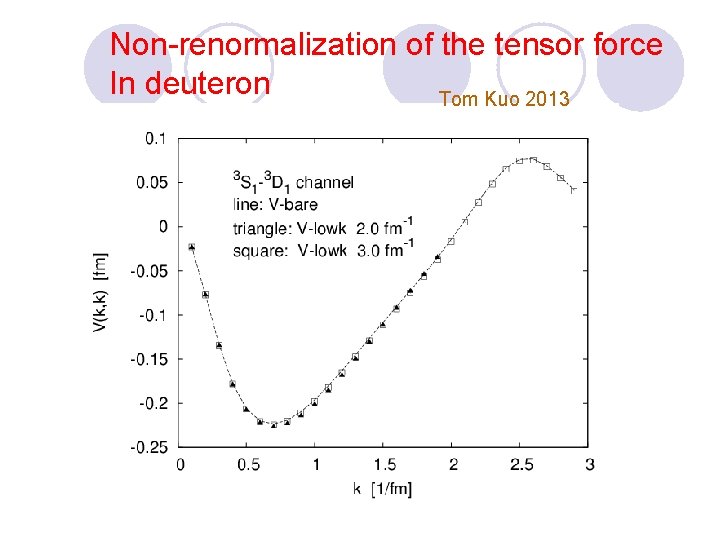
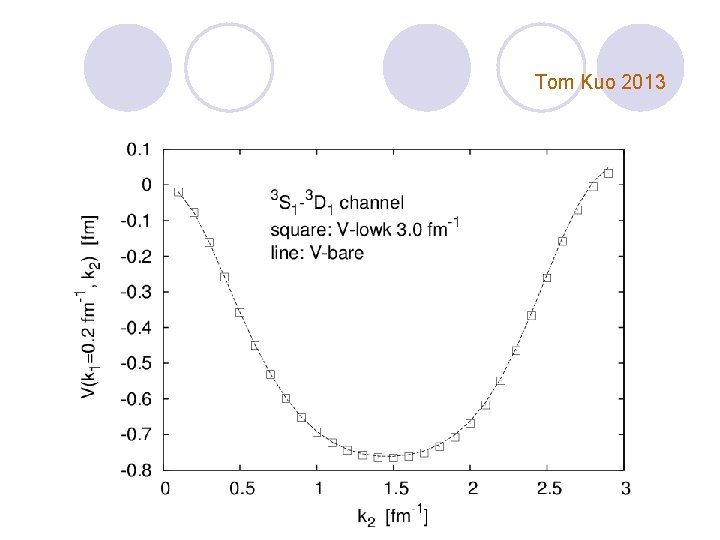
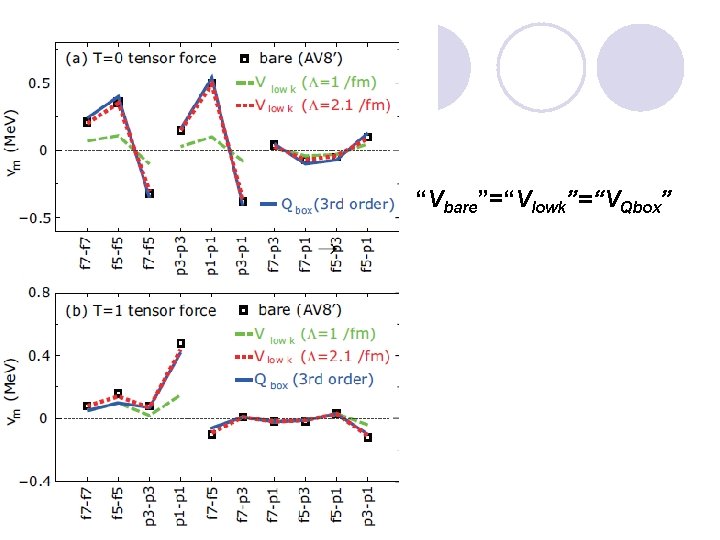
Observation but no proof Tensor forces are not renormalized !!

Non-renormalization of the tensor force In deuteron Tom Kuo 2013

Tom Kuo 2013

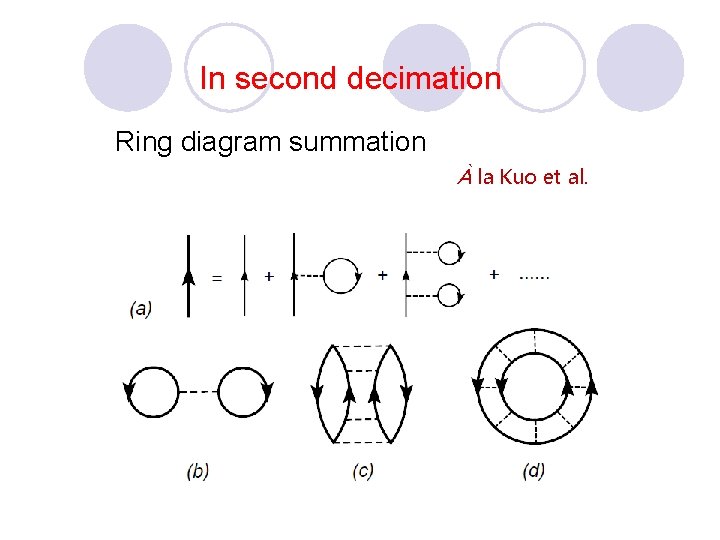
In second decimation Ring diagram summation À la Kuo et al.

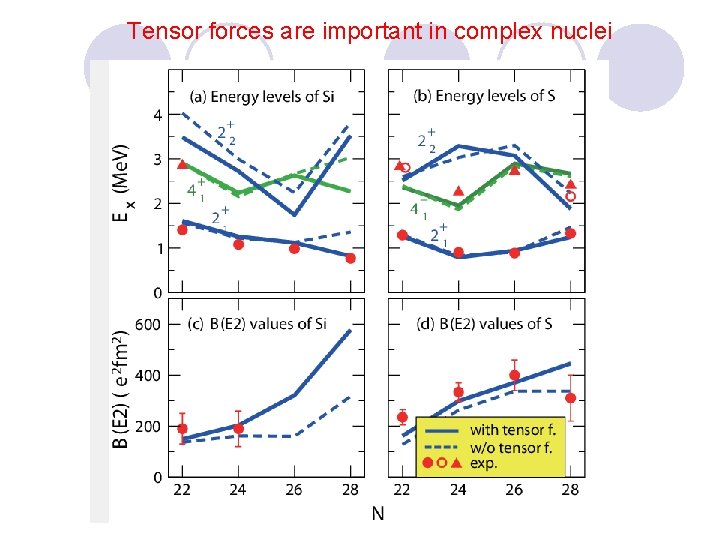
Tensor forces in shell evolution In exotic nuclei T. Otsuka 05 Monopole matrix element Evolution of single-particle energy

Tensor forces are important in complex nuclei

“Vbare”=“Vlowk”=“VQbox”

Conclusion In light as well as complex nuclei at low density involving no IDD, i. e. , . I take one step further and assume that the b remains zero independently of the IDD. This means that tensor forces with IDD’s for varying densities are non-renormalized.

How to “see” IDD v Tensor forces are “scale-independent” at any density, i. e. , fixed-point quantity. v If one can dial the density, then tensor forces will offer a pristine signal for IDD free of renormalization. v Zero-in on processes probing tensor forces.

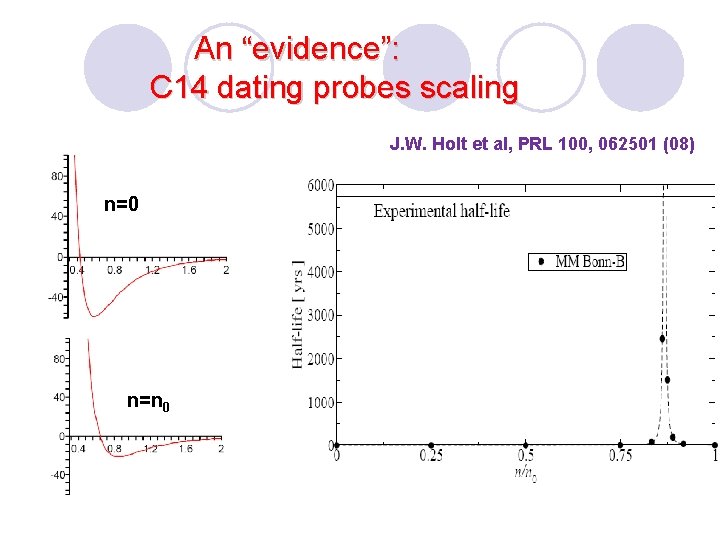
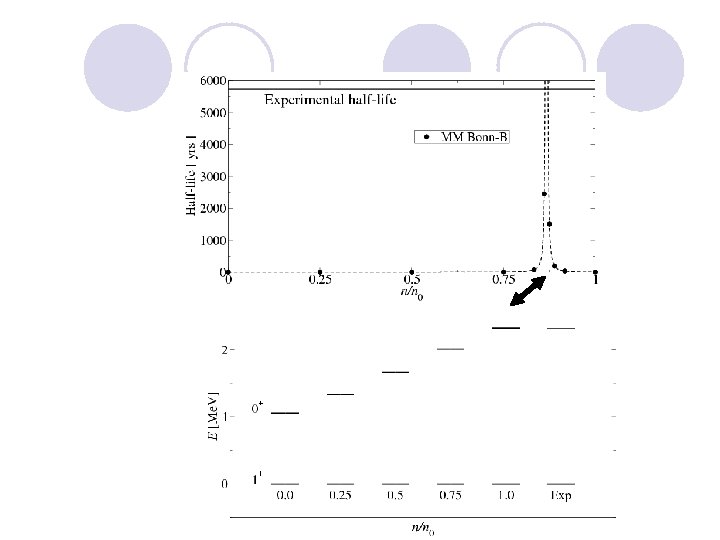
An “evidence”: C 14 dating probes scaling J. W. Holt et al, PRL 100, 062501 (08) n=0 n=n 0

Caveat? Many-body forces The long lifetime of C 14 has also been explained by 3 -body forces without IDD (Holt and Weise 2010, Maris et al 2011…). Way out: The contact 3 -body force (c) is of the same mass-scale as IDD. In medium with HLS, it is encoded in the IDD. With p + r exchange, the contact term should be negligible. (a) (b) (c)

What are the observables in RIB physics that can zero-in -- like in the C 14 case – on tensor forces acting in varying density regimes? If feasible, it will give a pristine signal if one can reach a density regime n 1/2 ~ 2 n 0.