Nuclear Spin Systems New applications of control Nuclear

Nuclear Spin Systems: New applications of control

Nuclear Magnetic Resonance • Many Atomic Nuclei have intrinsic angular momentum called spin. • The spin gives the nucleus a magnetic moment (like a small bar magnet). • The spins can be manipulated with radiofrequency electromagnetic fields. • Probing spins with rf fields and observing them gives information about chemical environment of the nuclei in a non-invasive way. Therefore field of nuclear magnetic resonance is the single most important analytical tool in chemistry.

• The magnetic moment of a single nuclear spin is too weak to detect. • The spins are therefore usually detected in the Bulk.

H M y x M

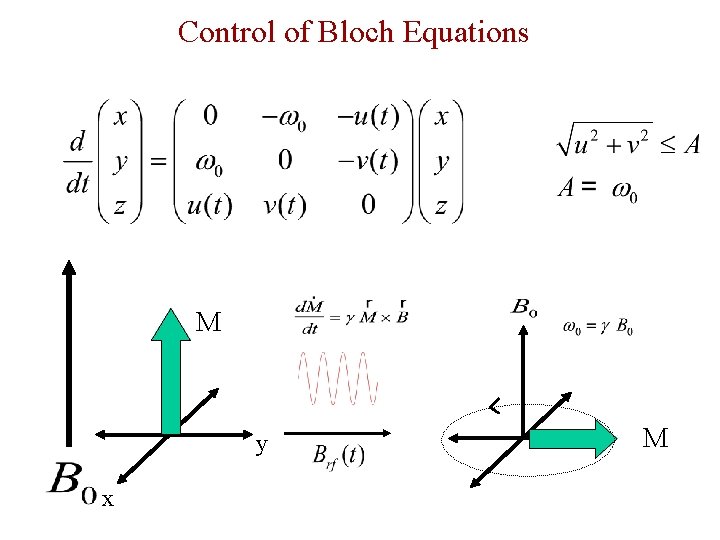
Control of Bloch Equations M y x M

Need for an Oscillatory Control

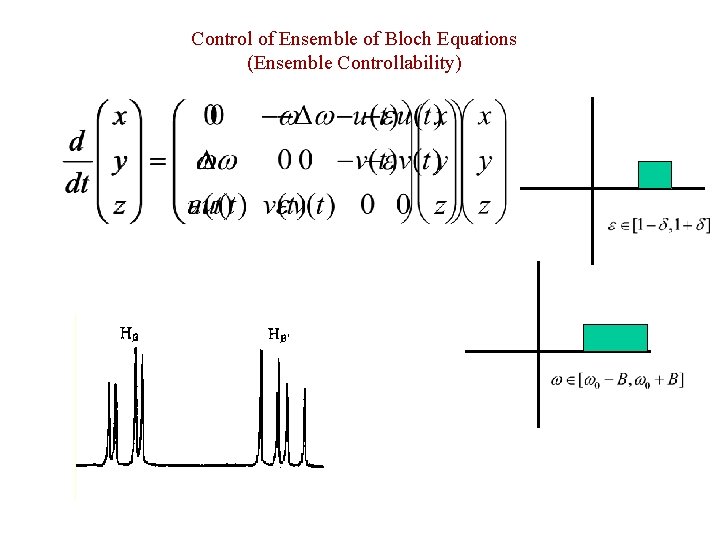
Control of Ensemble of Bloch Equations (Ensemble Controllability)

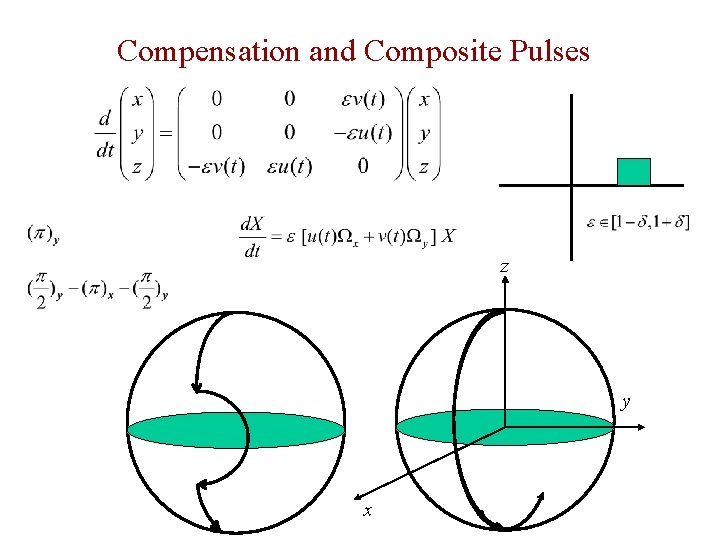
Compensation and Composite Pulses z y x

Lie Algebras and Polynomial Approximations

Lie Algebras and Polynomial Approximations Using Choose as generators such that it is approx. constant for

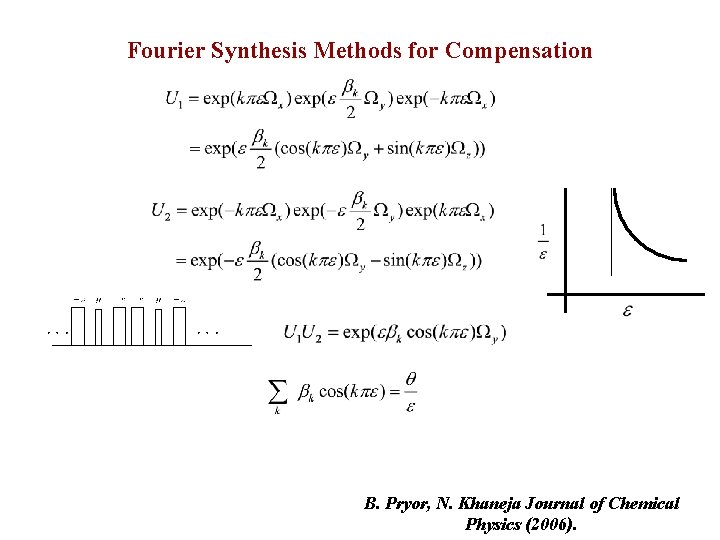
Fourier Synthesis Methods for Compensation B. Pryor, N. Khaneja Journal of Chemical Physics (2006).

Fourier Synthesis Methods for Compensation Ongoing work with M. Nimbalkar and S. J. Glaser

Some Negative Results Nil-Potent Systems Cannot be Compensated y x

Some Negative Results Linear systems cannot be compensated for field inhomogeneities

Ensemble Controllability of Bloch Equations J. S. Li and N. Khaneja, PRA (2006)

Ensemble Controllability of Bloch Equations J. S. Li and N. Khaneja, PRA (2006)

Larmor Dispersion and Bounded Controls Adiabatic Passage is Robust to rf-inhomogeneity

Control of Inhomogeneous Spin Ensembles M y x M

• Ensemble Control of Switched Bilinear Systems

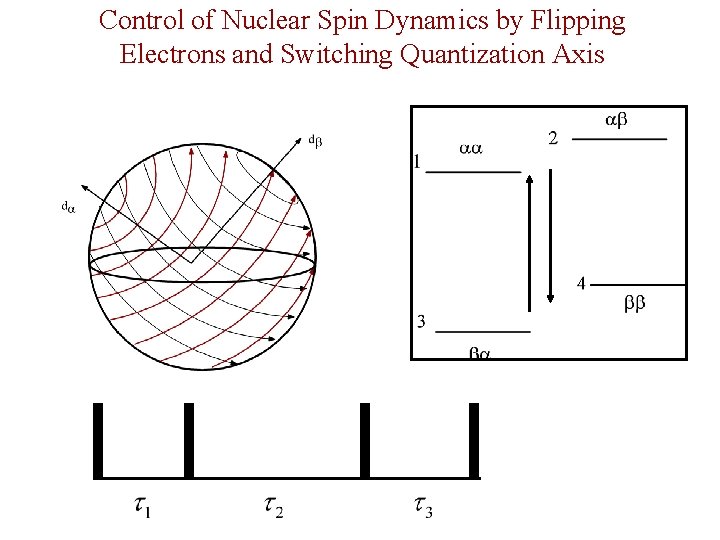
Switched Control of Electron Nuclear Spin Systems N. Khaneja PRA(2007)

Control of Nuclear Spin Dynamics by Flipping Electrons and Switching Quantization Axis

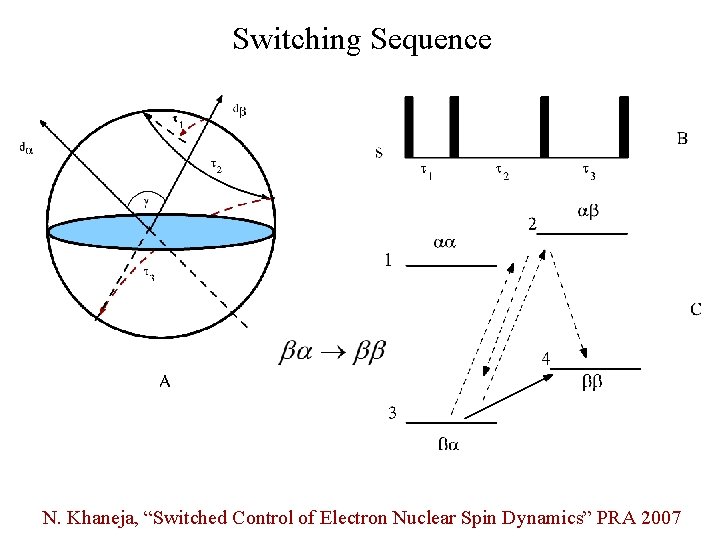
Switching Sequence N. Khaneja, “Switched Control of Electron Nuclear Spin Dynamics” PRA 2007

How many Switchings Algorithms known to find minimum number of switches

How many switchings if a controlled operations is desired ? Shortest Switched Loops with a given holonomy

Electron coupled to many Nuclear Spins See Jamin Sheriff’s Talk

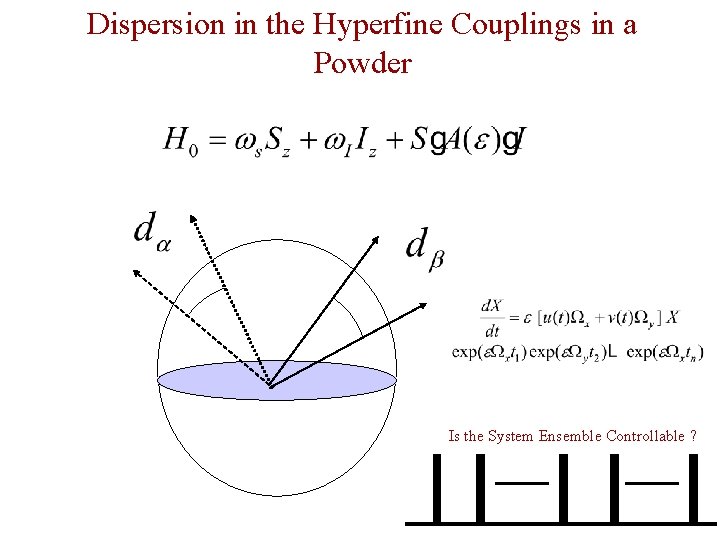
Dispersion in the Hyperfine Couplings in a Powder Is the System Ensemble Controllable ?

M y x M

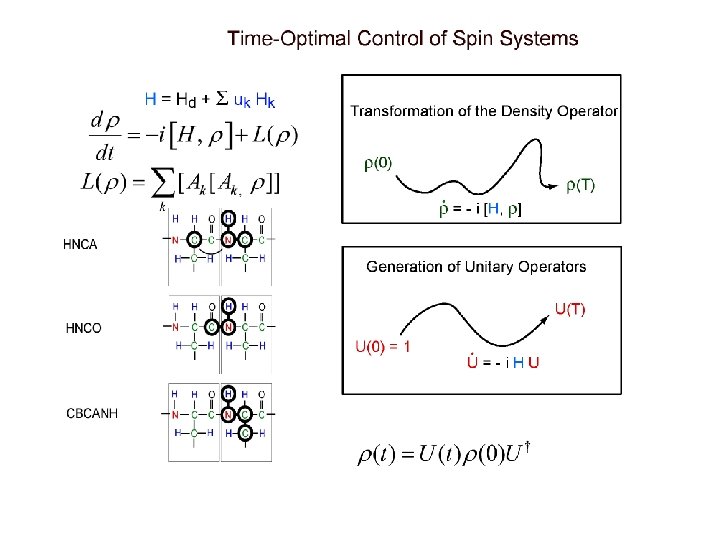
Manipulation of Coupled Spin Dynamics S I Relaxation Optimized Coherent Spectroscopy Singular Optimal Control Problems

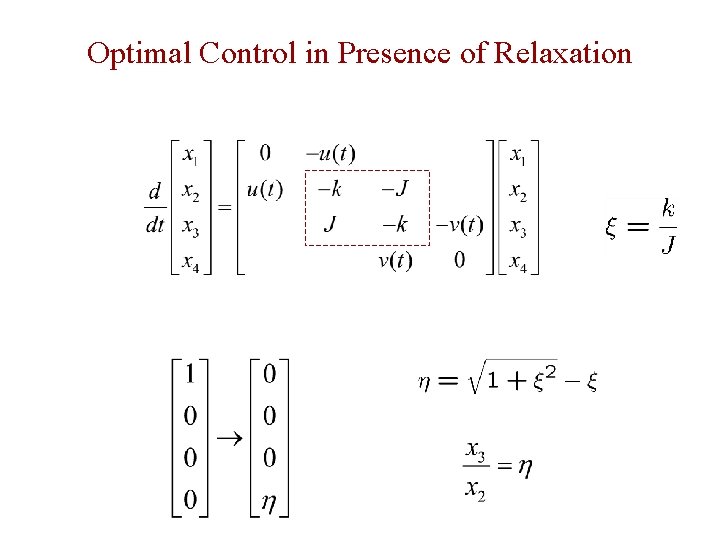
Optimal Control in Presence of Relaxation

Reducing the singular control problem

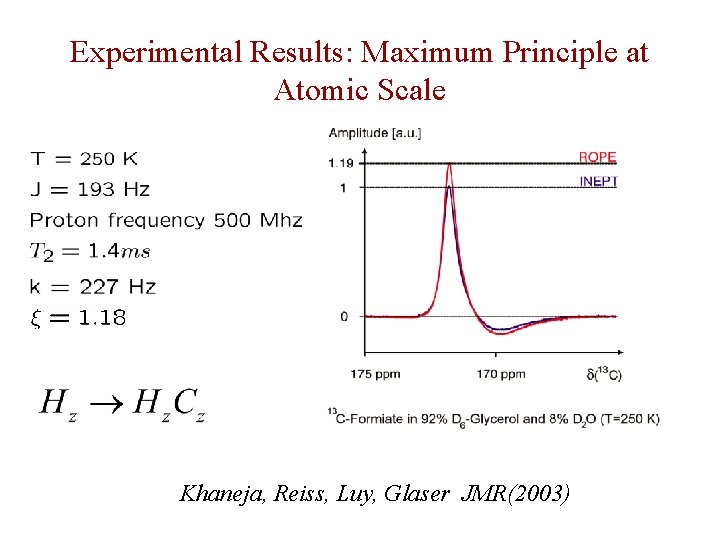
Experimental Results: Maximum Principle at Atomic Scale Khaneja, Reiss, Luy, Glaser JMR(2003)

Control of Spin Networks are excellent examples of Bilinear Control systems with Dissipation. Computing reachable sets and optimal controls are of both practical and theoretical interest.

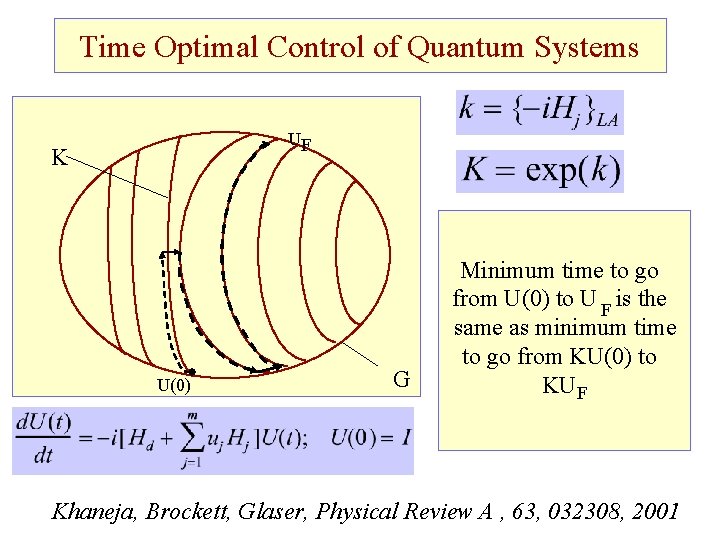
Time Optimal Control of Quantum Systems UF K U(0) G Minimum time to go from U(0) to U F is the same as minimum time to go from KU(0) to KUF Khaneja, Brockett, Glaser, Physical Review A , 63, 032308, 2001

Control Systems on Coset Spaces G/K is a Riemannian Symmetric Space The velocities of the shortest paths in G/K always commute!

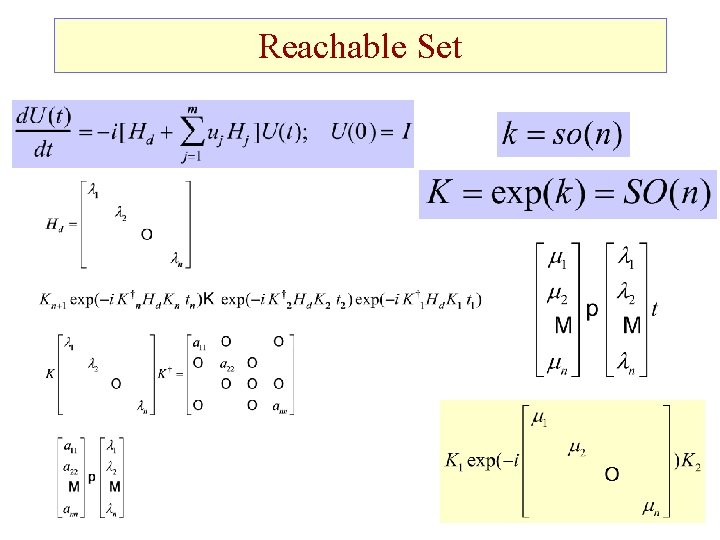
Reachable Set

Cartan Decompositions , Two-Spin Systems and Canonical Decomposition of SU(4)

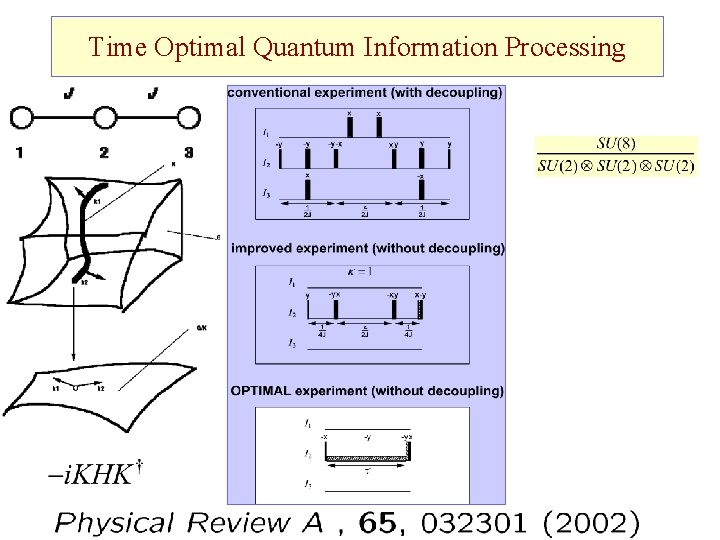
Time Optimal Quantum Information Processing

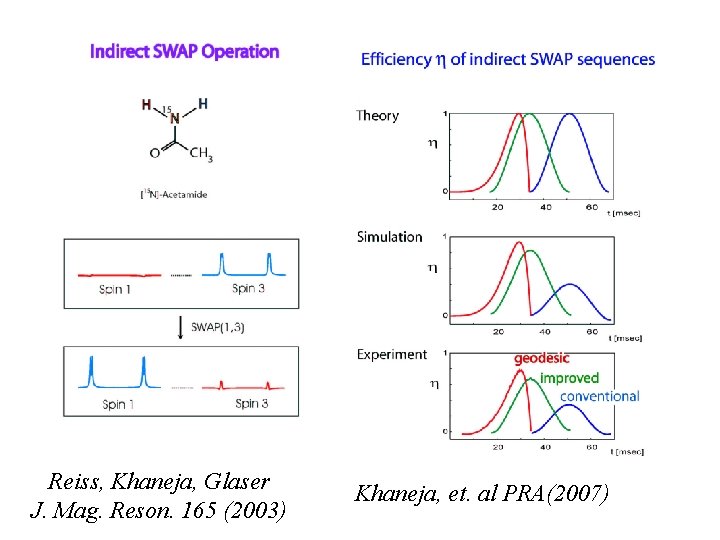
Reiss, Khaneja, Glaser J. Mag. Reson. 165 (2003) Khaneja, et. al PRA(2007)

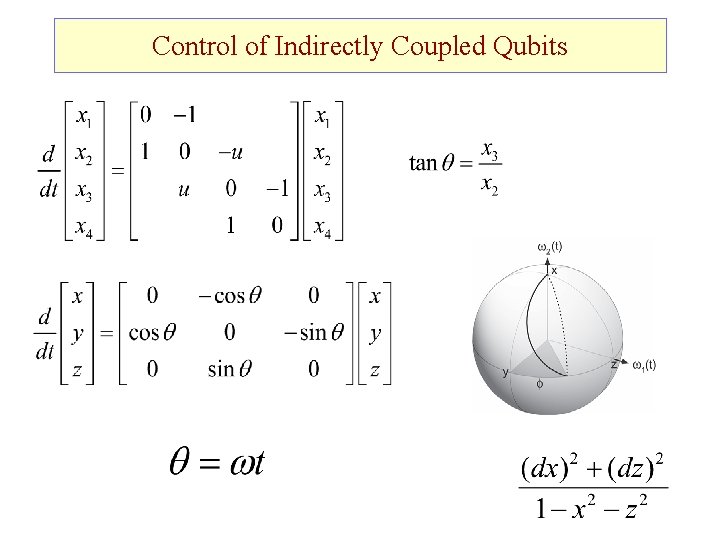
Control of Indirectly Coupled Qubits

Control of Indirectly Coupled Qubits

Dynamics of n-coupled Spins The dynamics of coupled spin ½ particles is described by an element of A basis of Lie algebra of can be expressed as tensor product of pauli spin matrices

• Control of Bilinear Control Systems with Periodic Drift

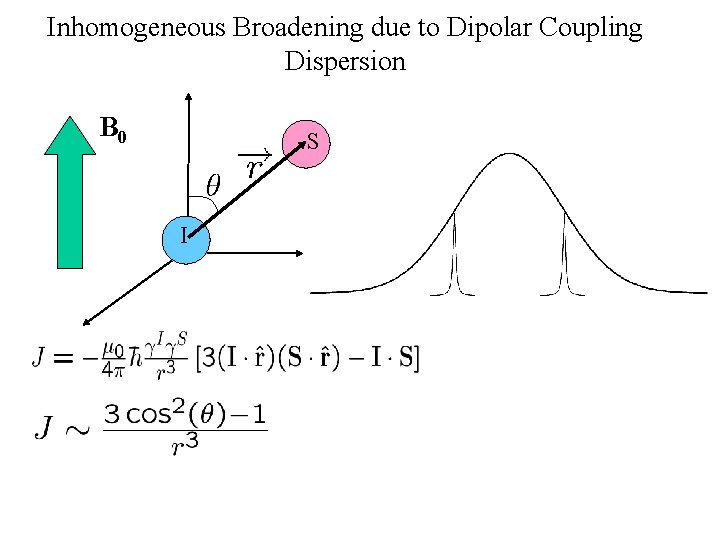
Inhomogeneous Broadening due to Dipolar Coupling Dispersion B 0 S I

Inhomogeneous broadening by chemical shift anisotropy axial symmetry (h = 0)

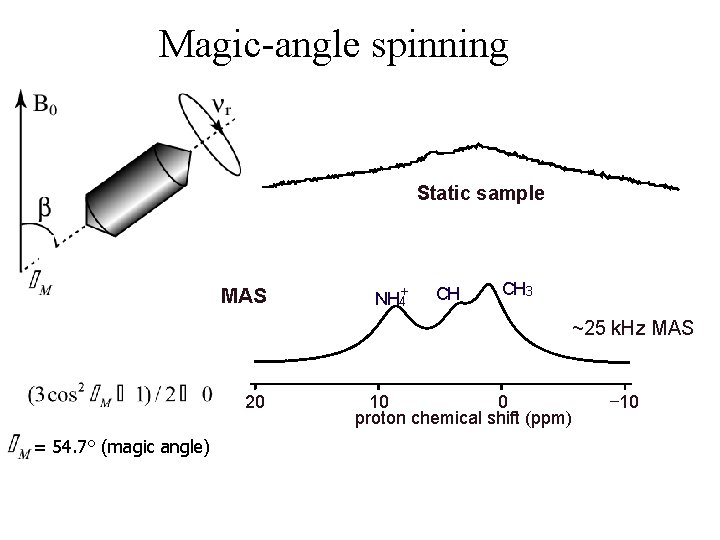
Magic-angle spinning Static sample MAS NH 4+ CH CH 3 ~25 k. Hz MAS 20 = 54. 7° (magic angle) 10 0 proton chemical shift (ppm) -10

x z y

Broadband Control x z y

Broadband control in biological solid-state NMR J. Am. Chem. Soc. , 126 (2005) Chem. Phys. Letter (2005) Journal of Chemical Physics (2006) B S OCDCP I DCP HORROROCHORROR

Conclusion • I hope, I may have convinced you that control and manipulation of spins is a fertile ground for new problems and developments in bilinear/geometric control theory. • We introduced and motivated the notion of ensemble controllability. • We showed how problems of control of dissipative bilinear control systems and time optimal control on Lie Groups arise naturally in control of spin systems. • If you find all this exciting, walk over to the chemistry or physics department and convince a colleague that you have a better pulse sequence than anything else in the field as it comes from maximum principle ! • We showed examples of Switched Control Systems and Bilinear Control Systems with periodic drift. • Thanks for your attention.