Nuclear Norm Heuristic for Rank Minimization Guaranteed MinimumRank

Nuclear Norm Heuristic for Rank Minimization Guaranteed Minimum-Rank Solutions of Linear Matrix Equations via Nuclear Norm Minimization Necessary and Sufficient Conditions for Success of the Nuclear Norm Heuristic for Rank Minimization Presenter: Zhen Hu

Outline ■ ■ ■ Introduction From Compressed Sensing to Rank Minimization Restricted Isometry and Recovery of Low-Rank Matrices Algorithms for Nuclear Norm Minimization Necessary and Sufficient Conditions for Success of the Nuclear Norm Heuristic for Rank Minimization ■ Discussion and Future Developments 2 2/21/2021

Introduction ■ An affine rank minimization problem ■ Minimization of the l 1 norm is a well known heuristic for the cardinality minimization problem. ■ L 1 heuristic can be a priori guaranteed to yield the optimal solution. ■ The results from the compressed sensing literature might be extended to provide guarantees about the nuclear norm heuristic for the more general rank minimization problem. 3 2/21/2021

From Compressed Sensing 4 2/21/2021

Matrix Norm ■ Frobenius Norm ■ Operator Norm ■ Nuclear Norm 5 2/21/2021

Convex Envelopes of Rank and Cardinality Functions 6 2/21/2021

Additive of Rank and Nuclear Norm 7 2/21/2021

Nuclear Norm Minimization ■ This problem admits the primal-dual convex formulation ■ The primal-dual pair of semidefinite programs 8 2/21/2021

Restricted Isometry and Recovery of Low Rank Matrices 9 2/21/2021

Nearly Isometric Families 10 2/21/2021

11 2/21/2021

Main Results 12 2/21/2021

Main Results 13 2/21/2021

The trade-offs between computational speed and guarantees on the accuracy of the resulting solution. Algorithms for Nuclear Norm Minimization ■ Interior Point Methods for Semidefinite Programming □ For small problems where a high-degree of numerical precision is required, interior point methods for semidefinite programming can be directly applied to solve affine nuclear minimization problems. ■ Projected Subgradient Methods ■ Low-rank Parametrization ■ SDPLR and the Method of Multipliers 14 2/21/2021

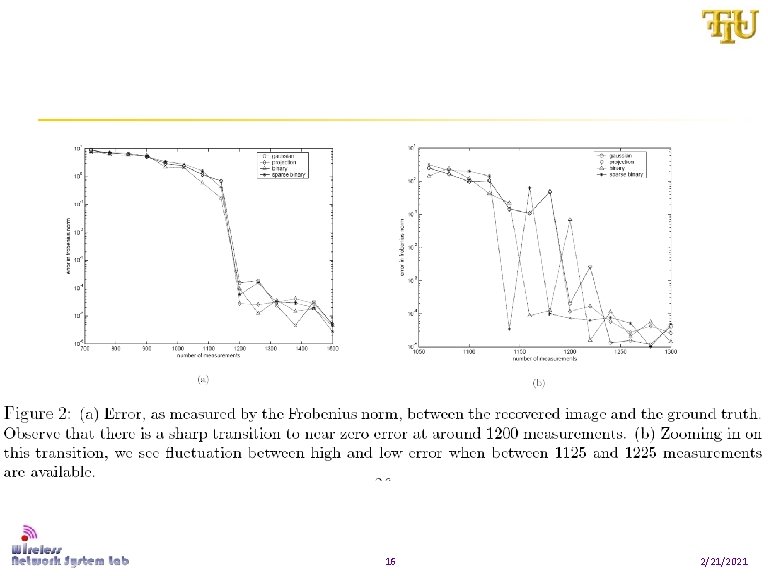
Numerical Experiments 15 2/21/2021

16 2/21/2021

Necessary and Sufficient Conditions ■ The authors present a necessary and sufficient condition for the solution of the nuclear norm heuristic to coincide with the minimum rank solution in an affine space. ■ The condition characterizes a particular property of the null space of the linear map which defines the affine space. ■ The authors also present a reduction of the standard Linear Matrix Inequality (LMI) constrained rank minimization problem to a rank minimization problem with only equality constraints. 17 2/21/2021

■ Moreover, the authors show that when the linear map defining the constraint set is generated by sampling its entries independently from a Gaussian distribution, the null-space characterization holds with overwhelming probability provided the dimensions of the equality constraints are of appropriate size. ■ The authors provide numerical experiments demonstrating that even when matrix dimensions are small, the nuclear norm heuristic does indeed always recover the minimum rank solution when the number of constraints is sufficiently large. 18 2/21/2021

Necessary and Sufficient Conditions ■ The main optimization problem under study is ■ The main concern is when the optimal solution coincides with the optimal solution of 19 2/21/2021

20 2/21/2021

Theorem 3. 1 ■ The following theorem generalizes this null-space criterion to a critical property that guarantees when the nuclear norm heuristic finds the minimum rank solution of A(X)=b for all values of the vector b. A particular property of the null space of the linear map 21 2/21/2021

Lemma 4. 1 ■ For the proof of Theorem 3. 1 22 2/21/2021

Theorem 3. 2 Reduction to the affine case! 23 2/21/2021

Weak Bound 24 Probabilistic generation of constraints satisfying null space characterization 2/21/2021

Strong Bound 25 2/21/2021

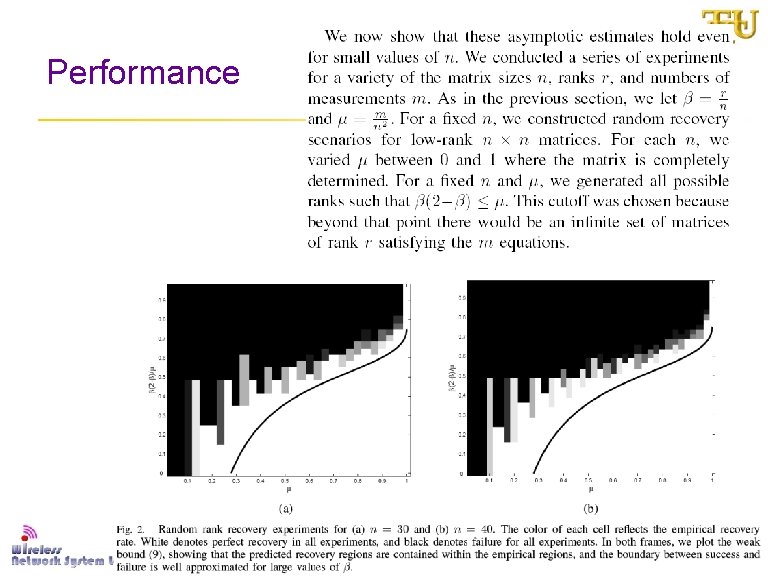
Performance 26 2/21/2021

Discussion ■ Having illustrated the natural connections between affine rank minimization and affine cardinality minimization, we were able to draw on these parallels to determine scenarios where the nuclear norm heuristic was able to exactly solve the rank minimization problem. ■ Future developments □ □ □ Factored measurements and alternative ensembles Noisy measurements and low rank approximation Incoherent ensembles and partially observed transforms Alternative numerical methods Geometric interpretations Parsimonious models and optimization 27 2/21/2021

Question? 28 2/21/2021