Nuclear Magnetic Resonance ANIMATED ILLUSTRATIONS MS Powerpoint Presentation

Nuclear Magnetic Resonance ANIMATED ILLUSTRATIONS MS Powerpoint Presentation Files Uses Animation Schemes as available in MS XP or MS 2003 versions A class room educational material File-8 FT NMR-I http: //ugc-inno-nehu. com/links_from_web. html

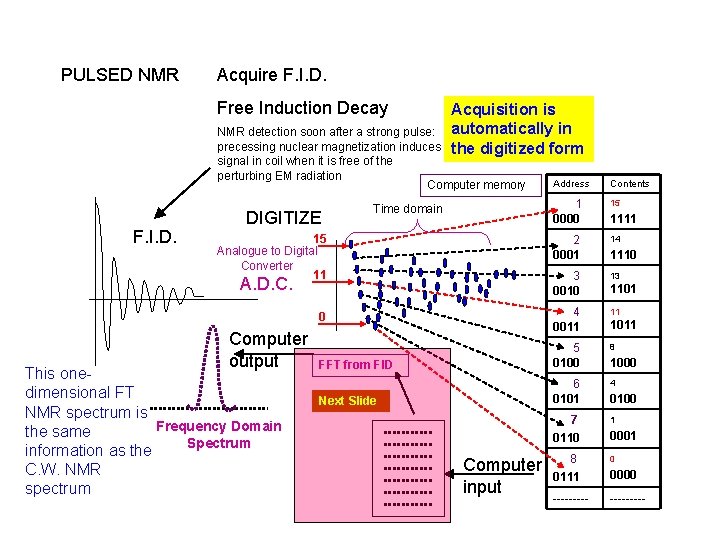
PULSED NMR Acquire F. I. D. Free Induction Decay Acquisition is NMR detection soon after a strong pulse: automatically in precessing nuclear magnetization induces a the digitized form signal in coil when it is free of the perturbing EM radiation F. I. D. Address Contents 1 0000 15 2 0001 14 3 0010 13 4 0011 11 8 FFT from FID 5 0100 4 Next Slide 6 0101 7 0110 1 8 0111 0 --------- DIGITIZE Computer memory Time domain 15 Analogue to Digital Converter 11 A. D. C. 0 Computer output This onedimensional FT NMR spectrum is Frequency Domain the same Spectrum information as the C. W. NMR spectrum Computer input 1111 1110 1101 1011 1000 0100 0001 0000

A program in Fortran for “Fast Fourier Transform” 1 11 Digitized FID Signal 13 Digital Computer -------------------------------------------------- FFT Program run OUTPUT 12 10 20 30 dimension A(50), B(50), Y(50), X(50) K=32 open (unit=1, file="output") Print 10, K DO 11 N=1, K X(N)=(N-1)*3. 5/K X(N)=EXP(-1. 0*X(N)) Y(N)=X(N)*(COS(2*3. 14*(N-1)*10. 0/K)+ COS(2*3. 14*(N-1)*4. 0/K)) write (1, 20) N, Y(N) DO 12 M=1, K A(M)=0 B(M)=0 DO 13 N=1, K-1 A(M)=A(M)+Y(N)*COS(2*3. 14*(M-1)*(N-1)/K) B(M)=B(M)+Y(N)*SIN(2*3. 14*(M-1)*(N-1)/K) A(M)=A(M)/K B(M)=B(M)/K M 2=M/2 write (1, 30) M 2, A(M 2), B(M 2) FORMAT(1 x, I 2, 2 x, F 10. 5) close (unit=1) STOP END

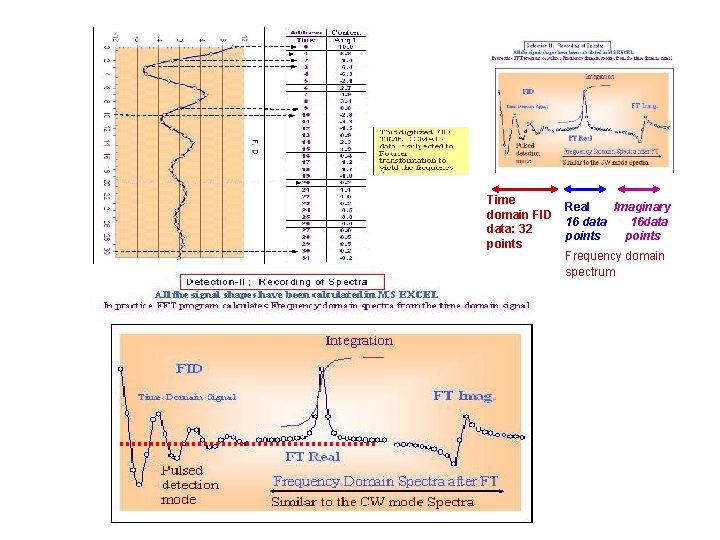
Time domain FID data: 32 points Real Imaginary 16 data 16 data points Frequency domain spectrum

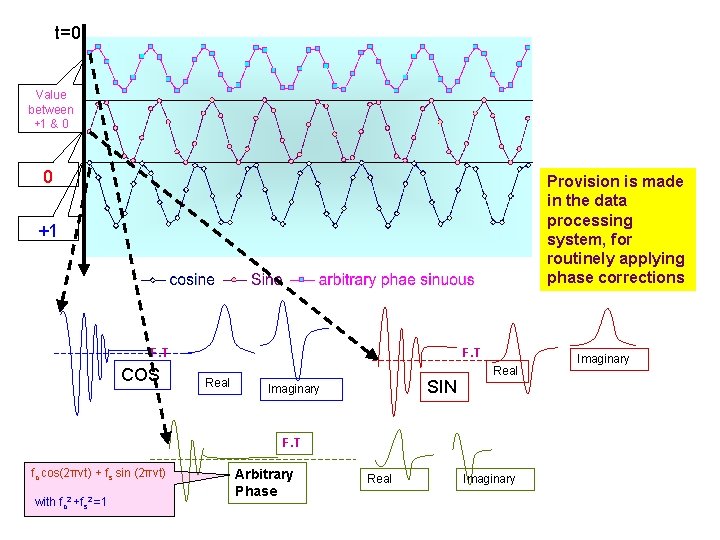
t=0 Value between +1 & 0 0 Provision is made in the data processing system, for routinely applying phase corrections +1 F. T COS F. T Real SIN Imaginary Real F. T fc cos(2πνt) + fs sin (2πνt) with fc 2 +fs 2 =1 Arbitrary Phase Real Imaginary