Nuclear Data and Materials Irradiation Effects Analysis of

Nuclear Data and Materials Irradiation Effects - Analysis of irradiation damage structures and multiscale modeling - Toshimasa Yoshiie Research Reactor Institute, Kyoto University

Comparison of irradiation effects between different facilities • Power reactors Research reactors • Neutron irradiation Ion irradiation Electron irradiation DPA (Displacement per atom) The number of displacement of one atom during irradiation DPA dose not represent the effect of cascades

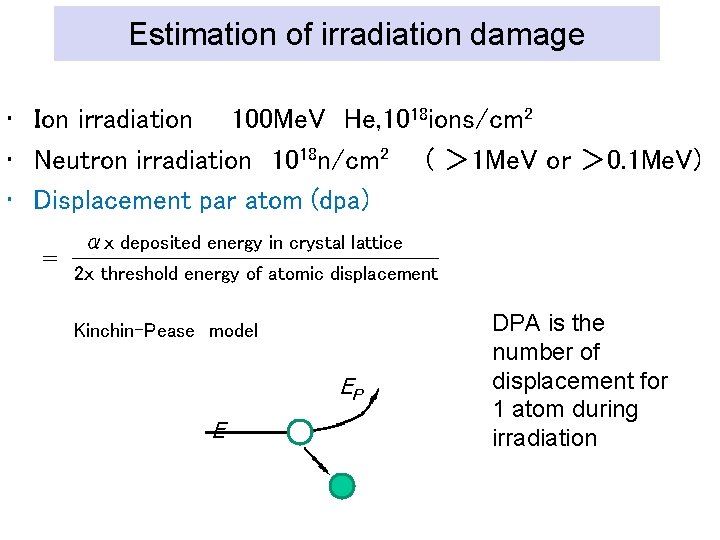
Estimation of irradiation damage • Ion irradiation　　100 Me. V　He, 1018 ions/cm 2 • Neutron irradiation　1018 n/cm 2　　( ＞ 1 Me. V or ＞ 0. 1 Me. V) • Displacement par atom (dpa) = αｘ deposited energy in crystal lattice 2ｘ threshold energy of atomic displacement 　　　　 Kinchin-Pease　model 　　　　EP E DPA is the number of displacement for 1 atom during irradiation

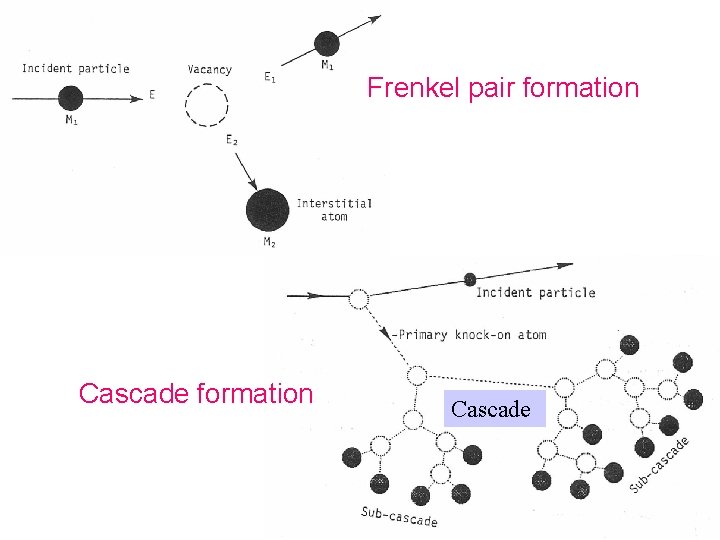
Frenkel pair formation Cascade

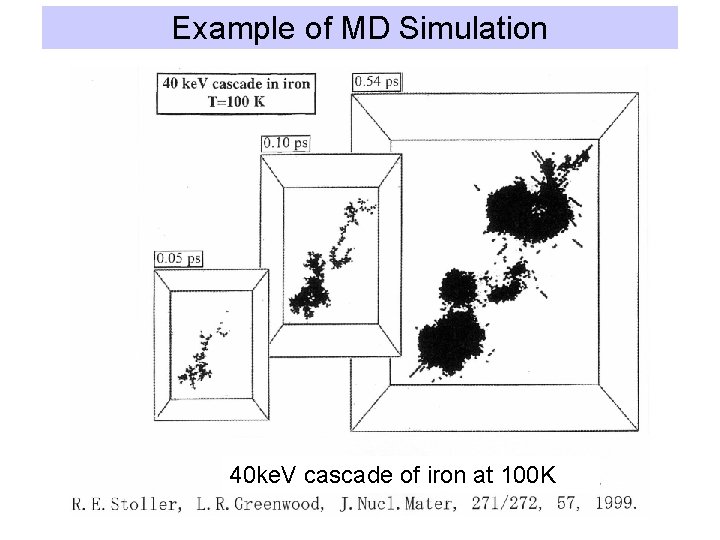
Example of MD Simulation 40 ke. V cascade of iron at 100 K

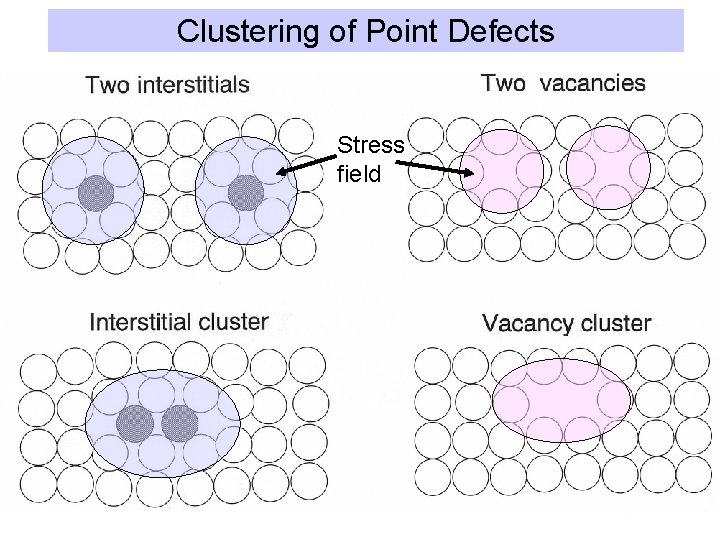
Clustering of Point Defects Stress field

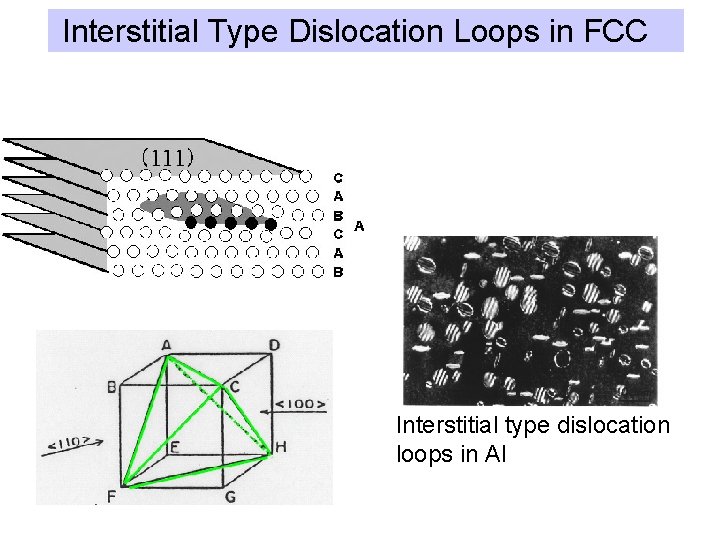
Interstitial Type Dislocation Loops in FCC　 Interstitial type dislocation loops in Al

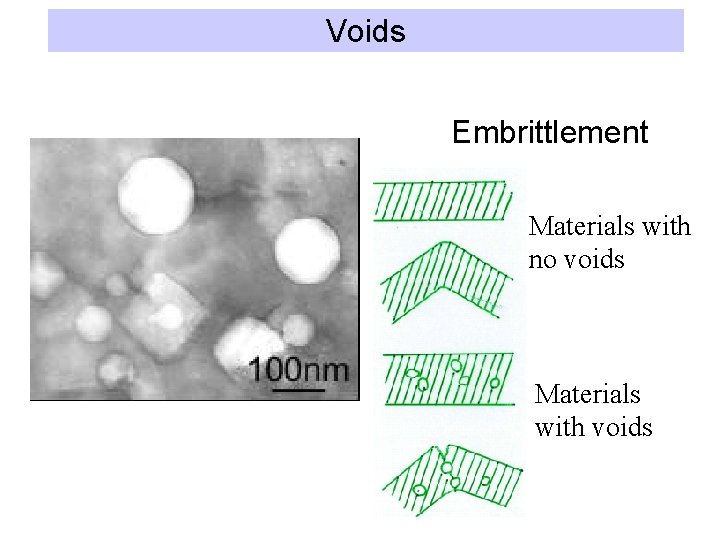
Voids Embrittlement Materials with no voids Materials with voids

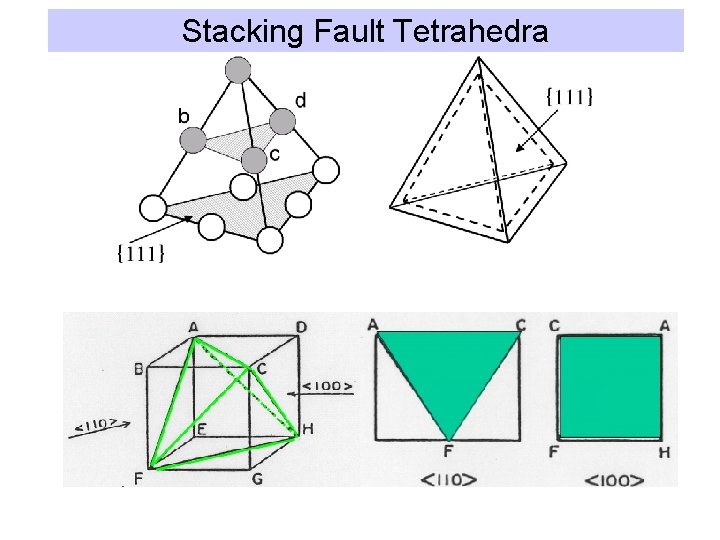
Stacking Fault Tetrahedra

Stacking Fault Tetrahedra

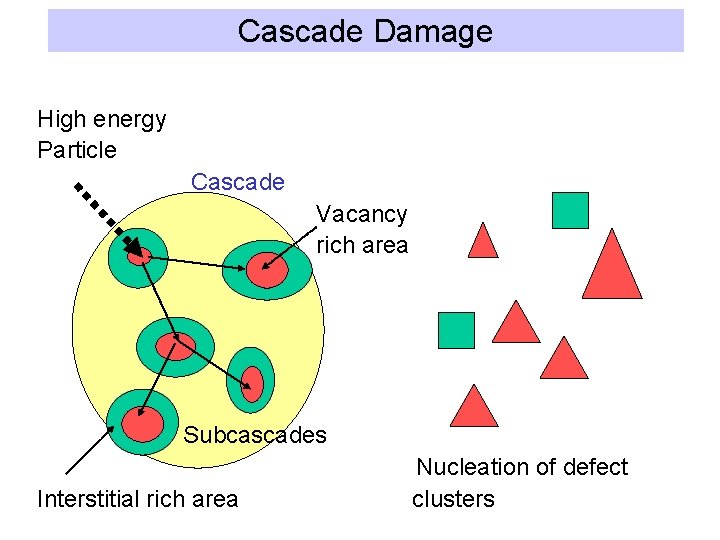
Cascade Damage High energy Particle Cascade Vacancy rich area Subcascades Interstitial rich area Nucleation of defect clusters

Comparison of Subcascade Structures by Thin Foil Irradiation 14 Me. V neutrons at 300 K. Neutron PKA

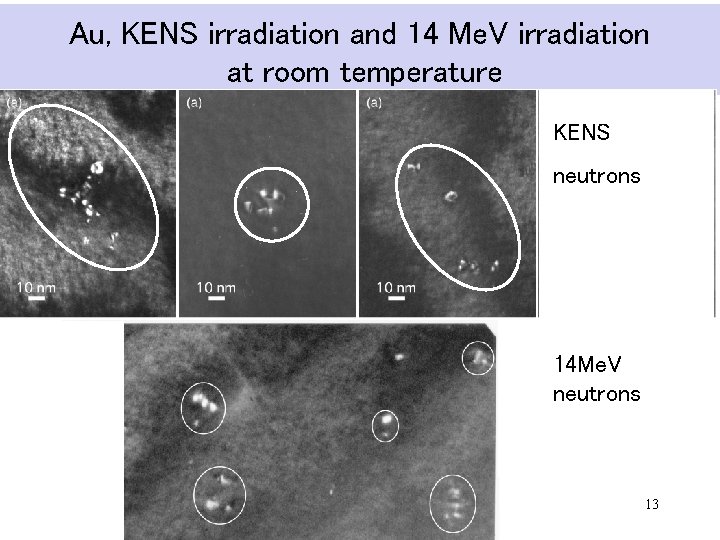
Au, KENS irradiation and 14 Me. V irradiation at room temperature KENS neutrons 14 Me. V　 neutrons 13

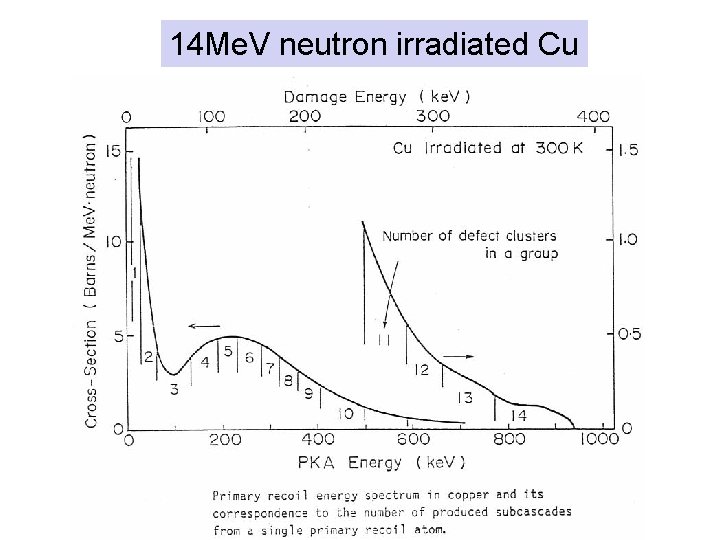
14 Me. V neutron irradiated Cu

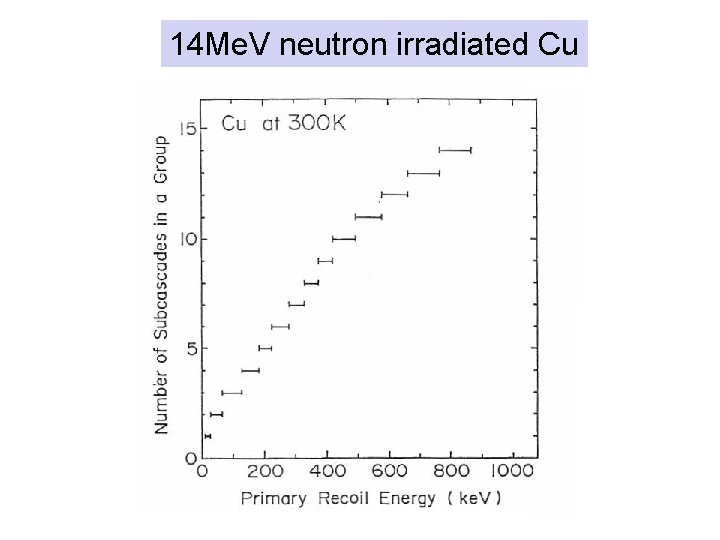
14 Me. V neutron irradiated Cu

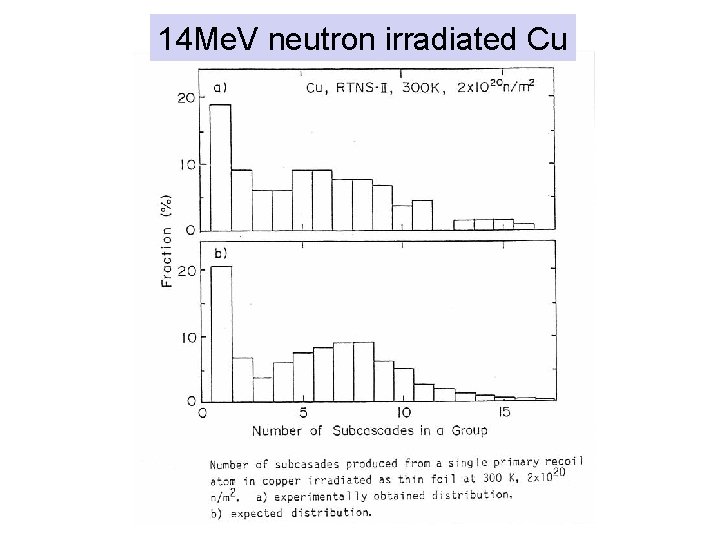
14 Me. V neutron irradiated Cu

14 Me. V neutron irradiated Cu

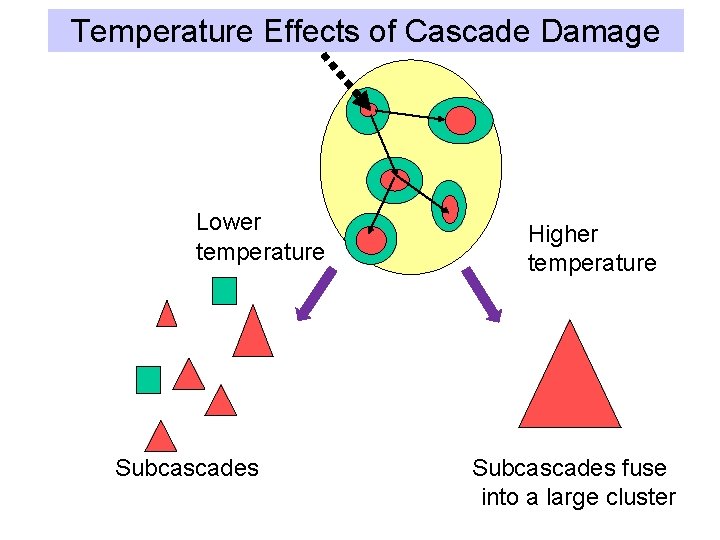
Temperature Effects of Cascade Damage Lower temperature Subcascades Higher temperature Subcascades fuse into a large cluster

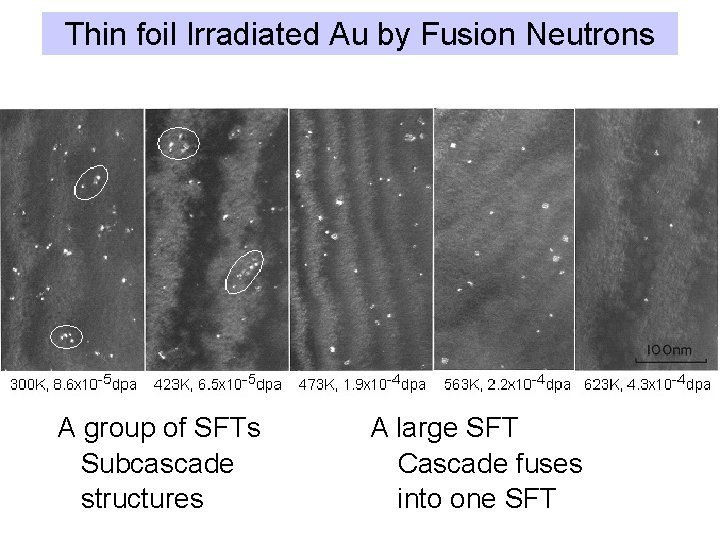
Thin foil Irradiated Au by Fusion Neutrons A group of SFTs Subcascade structures A large SFT Cascade fuses into one SFT

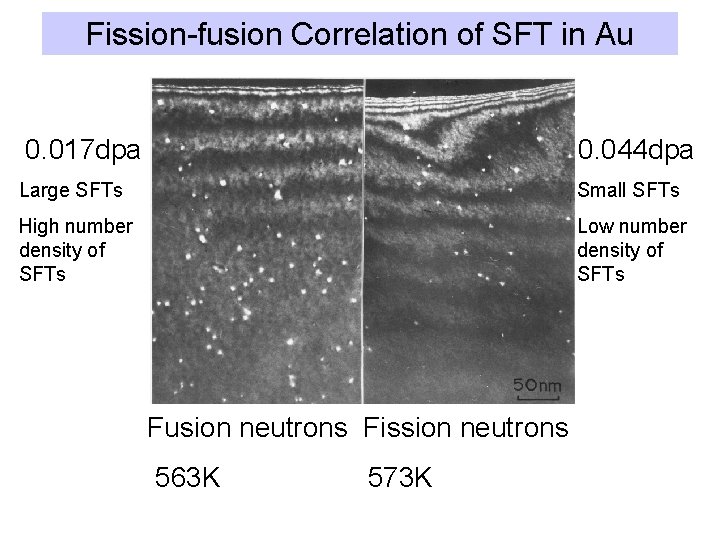
Fission-fusion Correlation of SFT in Au 0. 017 dpa 0. 044 dpa Large SFTs Small SFTs High number density of SFTs Low number density of SFTs Fusion neutrons Fission neutrons 563 K 573 K

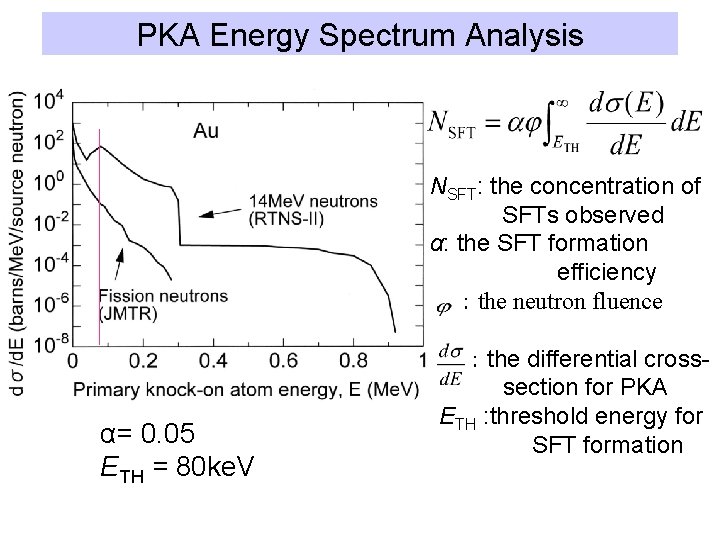
PKA Energy Spectrum Analysis NSFT: the concentration of 　　　SFTs observed α: the SFT formation 　　　efficiency ：the neutron fluence α= 0. 05 ETH = 80 ke. V 　：the differential crosssection for PKA ETH : threshold energy for SFT formation

MULTI-SCALE MODELING OF IRRADIATION EFFECTS IN SPALLATION NEUTRON SOURCE MATERIALS Toshimasa Yoshiie 1, Takahiro Ito 2, Hiroshi Iwase 3, Yoshihisa Kaneko 4, Masayoshi Kawai 3, Ippei Kishida 4, Satoshi 5 1 5 5, Kunieda , Koichi Sato 4 , Satoshi Shimakawa , Futoshi Shimizu 6, Tokio Fukahori 5, Satoshi Hashimoto , Naoyuki Hashimoto Yukinobu Watanabe 7, Qiu Xu 1, Shiori Ishino 8 2 Reactor Institute, Kyoto University　 Department of Mechanical Engineering, Toyohashi University of Technology High Energy Accelerator Research Organization Osaka City University 5 Japan Atomic Energy Agency 6 Hokkaido University 7 Kyushu University 8 Univerity of Tokyo 1 Research

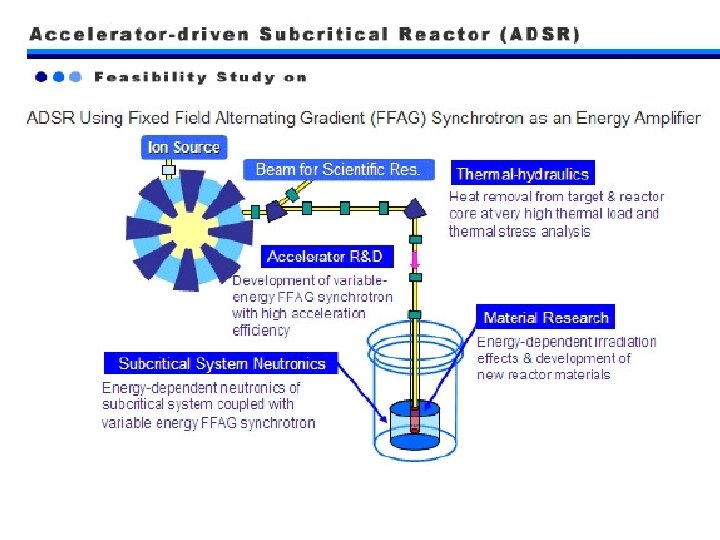
Motivation • Spallation neutron source and Accelerator Driven System (ADS) are a coupling of a target and a proton accelerator. High energy protons of Ge. V order irradiated in the target produce a large number of neutrons. • The beam window and the target materials thus subjected to a very high irradiation load by source protons and spallation neutrons generated inside the target. • At present, there are no materials that enable the window to be operational for the desired period of time without deterioration of mechanical properties.

Importance of Ge. V Order Proton Irradiation Effects in Materials • Spallation neutron source J-PARC (Japan) SNS (USA) • Accelerator driven system (in the planning stage ) 800 MW ADS (Minor Actinide transmutation, Japan Atomic Energy Agency) 5 MW Accelerator driven subcritical reactor (Kyoto University, neutron source)

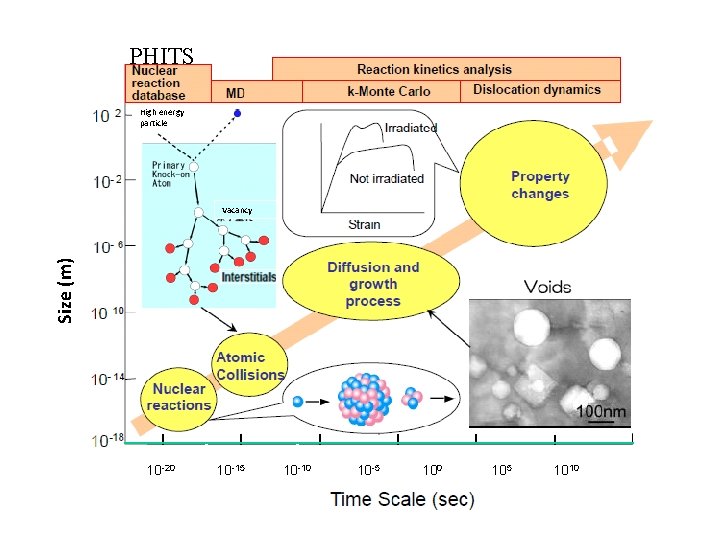
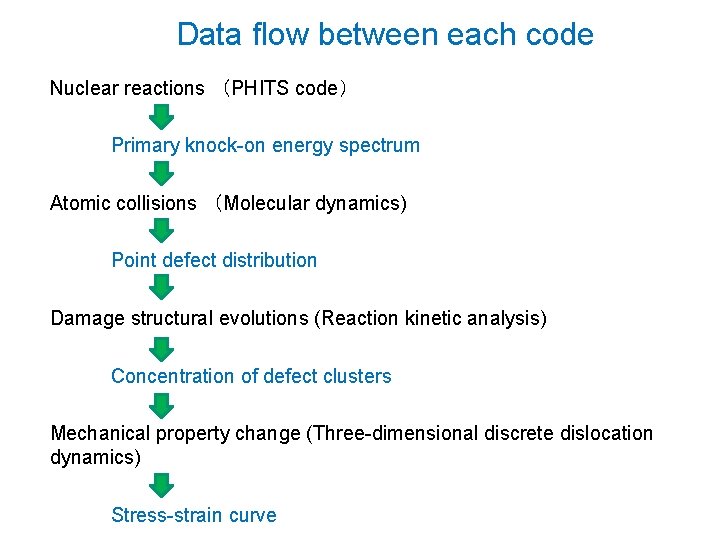
Purpose and outline • In this paper, mechanical property changes of nickel by 3 Ge. V protons were calculated by multi-scale modeling of irradiation effects. Nickel is considered to be a most simple model material of austenitic stainless steels used in beam window. The code consists of four parts. • Nuclear reaction, the interaction between high energy protons and nuclei in the target is calculated by PHITS code from 10 -22 s. • Atomic collision by particles which do not cause nuclear reactions is calculated by molecular dynamics and k-Monte Carlo. As the energy of particles is high, subcascade analysis is employed. In each subcascade, the direct formation of clusters and the number of mobile defects are estimated. • Damage structure evolution is estimated by reaction kinetic analysis. • Mechanical property change is calculated by using 3 D discrete dislocation dynamics (DDD). Stress-strain curves of high energy proton irradiated nickel are obtained.

PHITS High energy particle Size (m) Vacancy 　 10 -20　 10 -15　 10 -10　 10 -5　 100　 105　 1010

Data flow between each code Nuclear reactions （PHITS code） Primary knock-on energy spectrum Atomic collisions （Molecular dynamics) Point defect distribution Damage structural evolutions (Reaction kinetic analysis) Concentration of defect clusters Mechanical property change (Three-dimensional discrete dislocation dynamics) Stress-strain curve

1. Nuclear Reaction Nucleation rate of neutrons, photons, charged particles and PKA energy spectrum by them

Result of PHITS Simulation 3 Ge. V protons Ni Number of PKA energy (left) and energy deposition by PKA (right) in 3 Ge. V proton irradiated Ni of 3 mm in thickness.

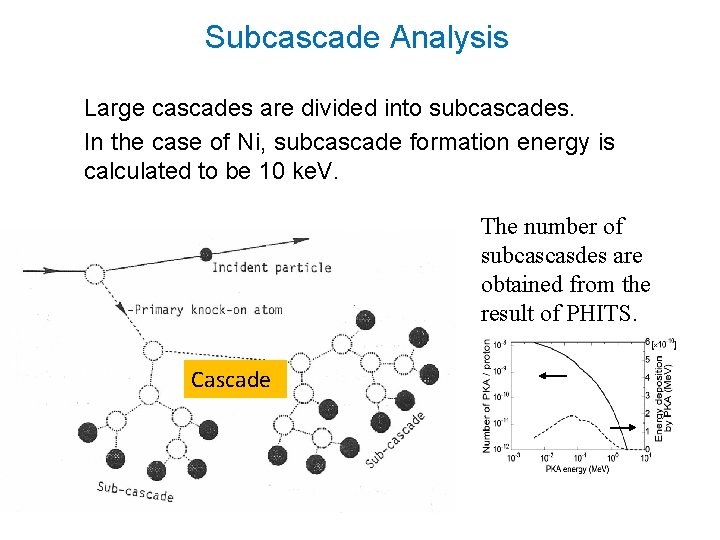
Subcascade Analysis Large cascades are divided into subcascades. In the case of Ni, subcascade formation energy is calculated to be 10 ke. V. The number of subcascasdes are obtained from the result of PHITS. Cascade

Number of subcascades by deposition of energy T 　　 TSC : Subcascade formation energy Total number of subcascades 　　　　　

2. Atomic Collision Simulation by MD Calculation Condition Ø Potential model by Daw and Baskes (1984) Ø NVE ensemble ( i. e. , number of the atoms, cell volume and energy were kept constant) Ø 35 x 35 lattices (171500 atoms) in a z simulation cell y Ø Periodic boundary condition for the x three directions 35 a 0 Ø Initial condition : equilibrium for 50 ps at 300 K, 0 MPa a 0 : lattice constant at 300 K Ø PKA energy： 10 ke. V Ø MD runs with different initial directions of PKA ( none of which were parallel to the lattice vector. )

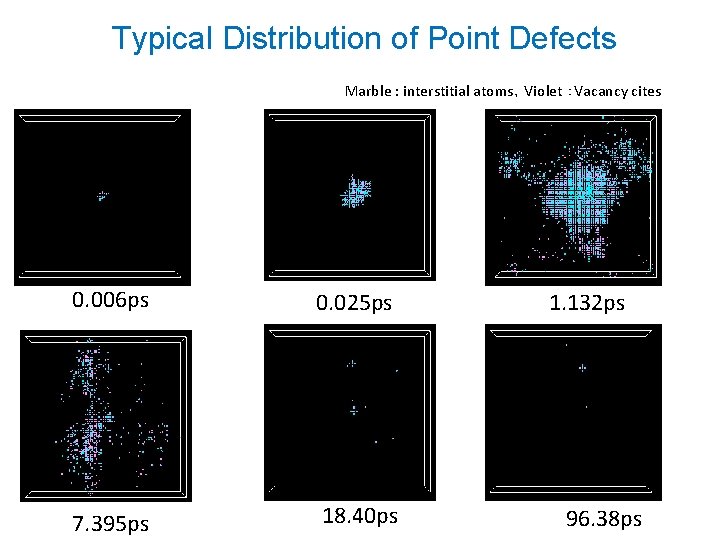
Typical Distribution of Point Defects Marble : interstitial atoms，Violet ：Vacancy cites 0. 006 ps 0. 025 ps 7. 395 ps 18. 40 ps 1. 132 ps 96. 38 ps

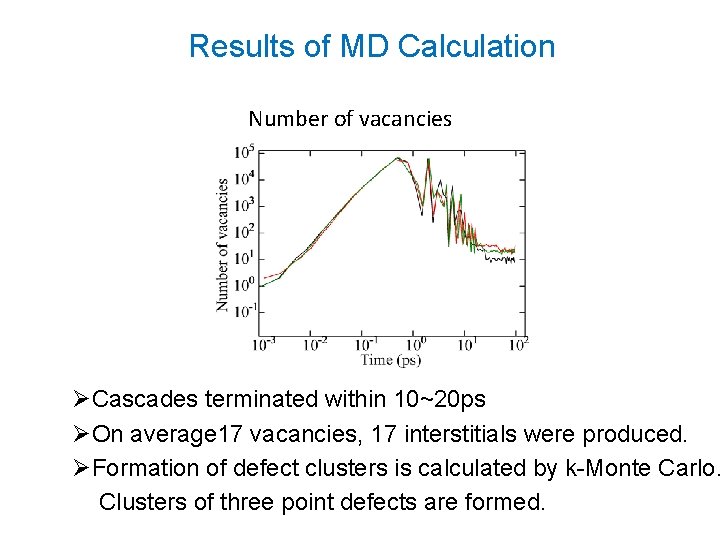
Results of MD Calculation Number of vacancies ØCascades terminated within 10~20 ps ØOn average 17 vacancies, 17 interstitials were produced. ØFormation of defect clusters is calculated by k-Monte Carlo. Clusters of three point defects are formed.

3. Damage Structure Evolution by Reaction Kinetic Analysis In order to estimate damage structural evolution, the reaction kinetic analysis is used. Assumptions used in the calculation are as follows: (1) Mobile defects are interstitials, di-interstitials, tri-interstitials, vacancies and divacancies. (2) Thermal dissociation is considered for di-interstitials, tri-interstitials di-vacancies and tri-vacancies, and point defect clusters larger than 4 are set for stable clusters. (3) Time dependence of 10 variables, concentration of interstitials, di-interstitials, triinterstitials, interstitial clusters (interstitial type dislocation loops), vacancies, divacancies, tri-vacancies, vacancy clusters (voids), total interstitials in interstitial clusters and total vacancies in vacancy clusters are calculated to 10 dpa. (4) Interstitial clusters (three interstitials) and vacancy clusters (three vacancies) are also formed directly in subcascades. (5) Materials temperature is 423 K during irradiation. The result is as follows, Formation of vacancy clusters of four vacancies, concentration: 0. 59 x 10 -3, Dislocation density: 1. 1 x 10 -9 cm/cm 3.

Reaction Kinetic Analysis CI : Interstitial concentration (fractional unit). CV : Vacancy concentration Z : Cross section of reaction M: Mobility damage production I-I recombination mutual annihilation　 absorption by loops absorption by voids annihilation of interstitials at sink

4. Estimation of Mechanical Property Changes (Plastic Deformation of Metals) t Plastic Deformation of Metals Dislocation Glide along Slip Planes t s Work Hardening ↓ Motions of Dislocation Lines e

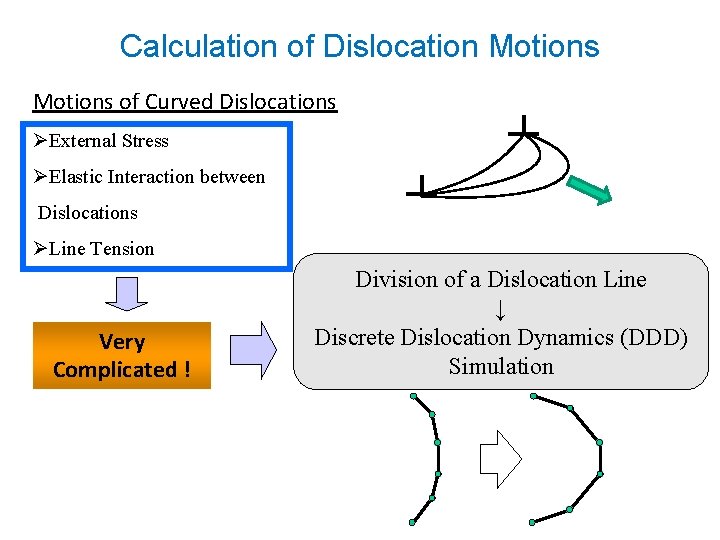
Calculation of Dislocation Motions of Curved Dislocations ØExternal Stress ØElastic Interaction between Dislocations ØLine Tension Very Complicated ! Division of a Dislocation Line ↓ Discrete Dislocation Dynamics (DDD) Simulation

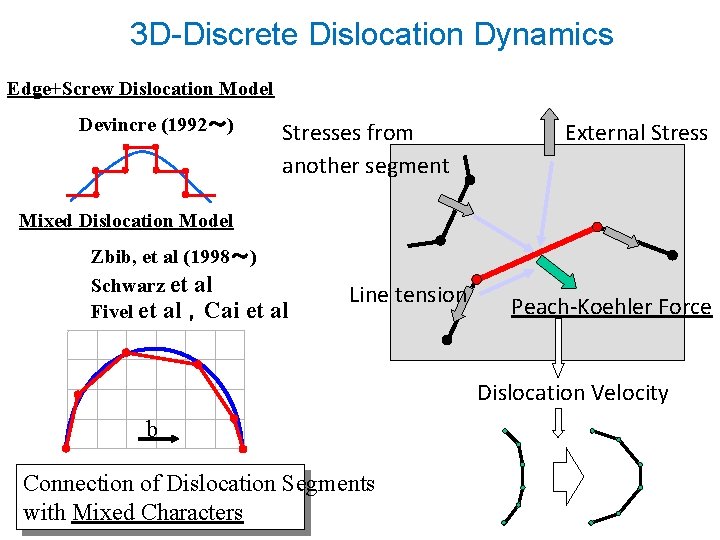
3 D-Discrete Dislocation Dynamics Edge+Screw Dislocation Model Devincre (1992～) Stresses from another segment External Stress Mixed Dislocation Model Zbib, et al (1998～) Schwarz et al Fivel et al ，Cai et al Line tension Peach-Koehler Force Dislocation Velocity b Connection of Dislocation Segments with Mixed Characters

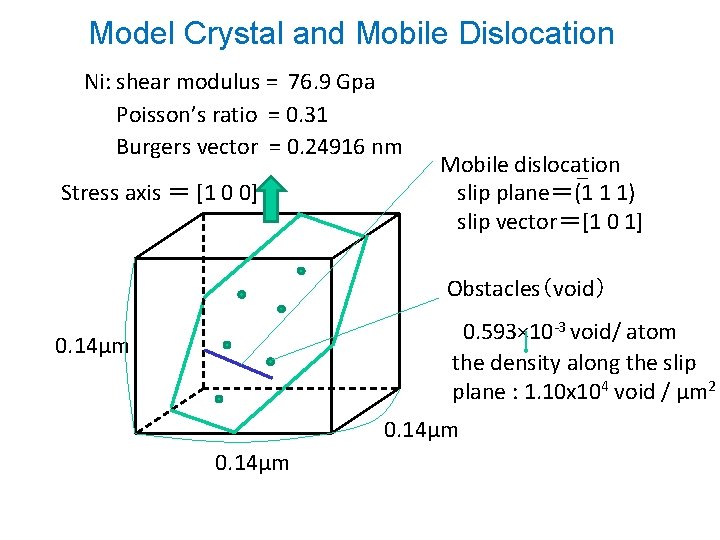
Model Crystal and Mobile Dislocation Ni: shear modulus = 76. 9 Gpa Poisson’s ratio = 0. 31 Burgers vector = 0. 24916 nm Stress axis ＝ [1 0 0] Mobile dislocation slip plane＝(1 1 1) slip vector＝[1 0 1] Obstacles（void） 　0. 593× 10 -3 void/ atom the density along the slip plane : 1. 10 x 104 void / μm 2 0. 14μm

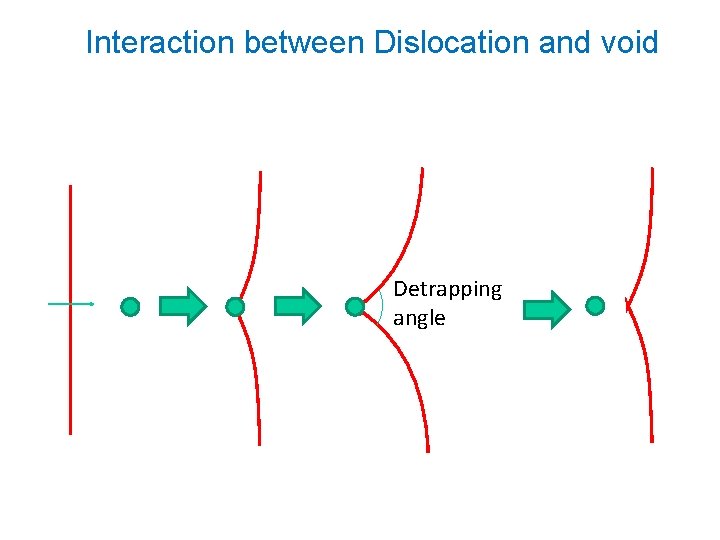
Interaction between Dislocation and void Detrapping angle

Determination of Detrapping Angle (Statistic Energy Calculation Method) ( l l l) void (Ī Ī 2) (Ī l 0) [lll] [ Ī Ī 2] [ Ī l 0] Stress Size and orientation of model lattice used for Static energy calculation of dislocation movement. b is the Burgers vector. Stable atomic position is determined by an effective medium theory (EMT) potential for Ni fitted by Jacobsen et al. [K. W. Jacobsen, P. Stoltze, J. K. Norskov, Surf. Sci. 366 (1996) 394].

Determination of Detrapping Angle between Edge Dislocations and 4 Vacancies Motion of dislocation near the slip plane under shear stress. X axis and Y axis are by atomic distance. In the left figure, a dislocation is separated into two partials. Four vacancies are at (16. 0, 0. 722, -0. 408), (15. 5, -0. 144, -0. 408), (16. 0, 0. 144, 0. 408) and (15. 5, 1. 01, 0. 408). Other figures indicate only right partial. 65 °

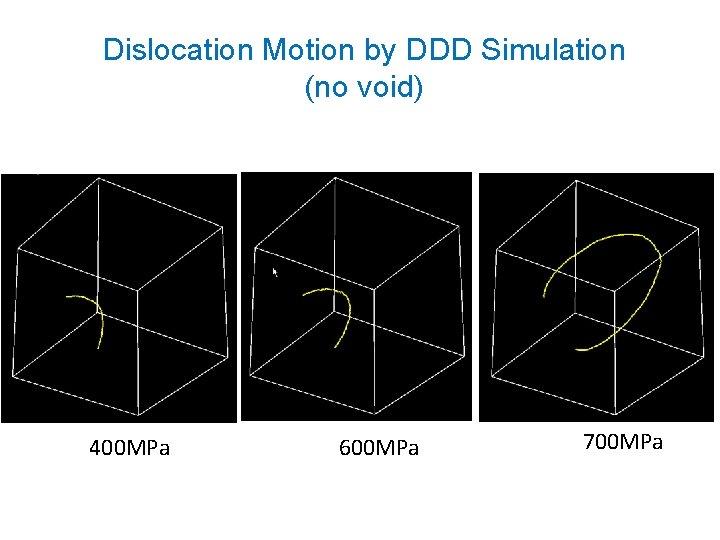
Dislocation Motion by DDD Simulation (no void) 400 MPa 600 MPa 700 MPa

Dislocation motion in the crystal with randomly-distributed voids Normal stress 0 MPa 200 MPa 300 MPa 400 MPa 500 MPa 650 MPa 700 MPa 750 MPa 800 MPa

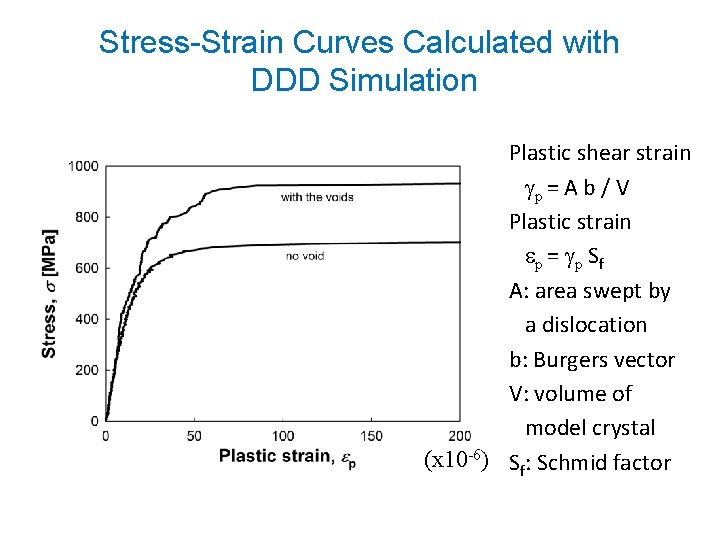
Stress-Strain Curves Calculated with DDD Simulation Plastic shear strain 　gp = A b / V Plastic strain 　ep = gp Sf A: area swept by 　a dislocation b: Burgers vector V: volume of 　model crystal (x 10 -6) Sf: Schmid factor

Summary Importance of nuclear data for materials irradiation effects was shown. DPA is not good measure of irradiation damage. PKA energy spectrum is more useful to analyze damage structures. As an example of the analysis, the mechanical property change in Ni by 3 Ge. V proton irradiation was calculated and preliminary results were obtained. Nuclear reactions : PHITS PKA energy spectrum Atomic collision : MD, k-Monte Carlo, Subcascade analysis. The number of point defects and clusters in the subcascade Damage structure evolution : Reaction kinetic analysis Void density, Dislocation density Mechanical properties : Discrete dislocation dynamics Statistic energy calculation Stress strain curve

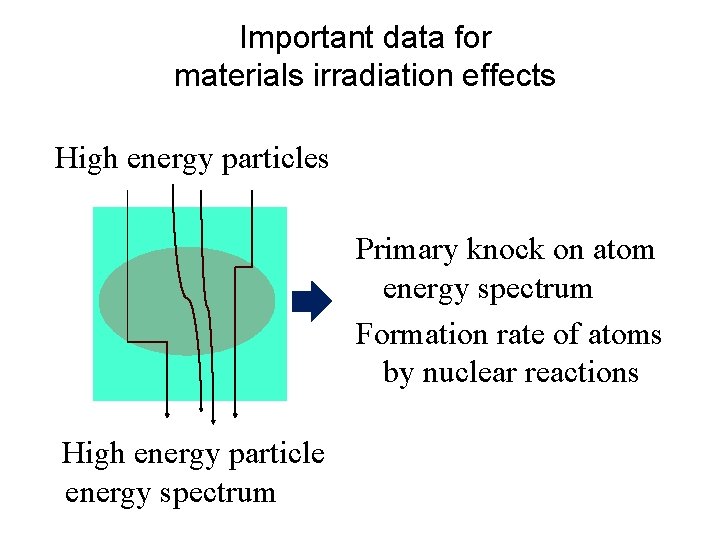
Important data for materials irradiation effects High energy particles Primary knock on atom energy spectrum Formation rate of atoms by nuclear reactions High energy particle energy spectrum