Nuclear Chemistry Types of Radiation Alpha a positively

Types of Radiation • Alpha (ά) – a positively charged (+2) helium isotope we

Other Nuclear Particles • Neutron • Positron – a positive electron • Proton –

Geiger Counter • Used to detect radioactive substances • Units of radiation is the

Half-Life • HALF-LIFE is the time that it takes for 1/2 a sample to

Half-Life Decay of 20. 0 mg of 15 O. What remains after 3 half-lives?

Kinetics of Radioactive Decay For each duration (half-life), one half of the substance decomposes.

Kinetics of Radioactive Decay A daughter N = N 0(1/2 )(t / t 1/2

A radioactive substance has a half-life of 20 minutes. If we begin with a

Now fill the first column with time increasing by half-life intervals Time elapsed 0

Now half the mass every time interval Time elapsed 0 20 40 60 80

The half-life of a material is 2 hours. If the initial count rate is

The half-life of a material is 3 hours. If the initial count rate is

Radiocarbon Dating 14 N 7 + 01 n 14 C 6 14 N 7

Learning Check! The half life of I-123 is 13 hr. How much of a

Slides: 20

Download presentation

Nuclear Chemistry

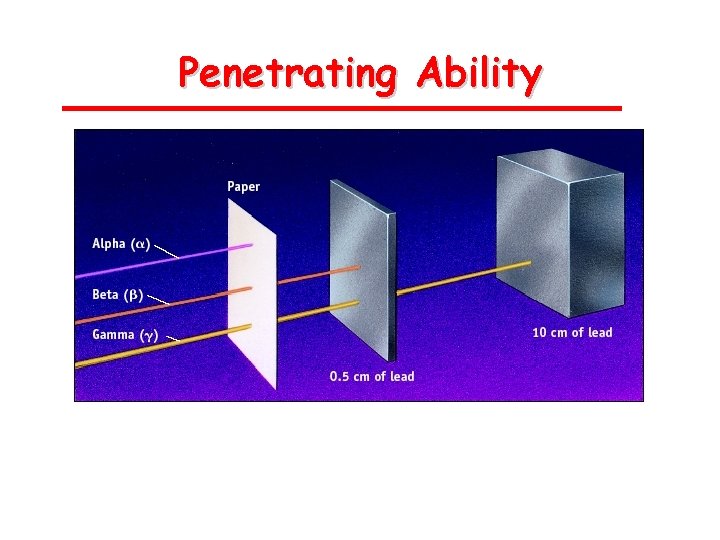
Types of Radiation • Alpha (ά) – a positively charged (+2) helium isotope we usually ignore the charge because it involves electrons, not protons and neutrons • Beta (β) – an electron • Gamma (γ) – pure energy; called a ray rather than a particle

Other Nuclear Particles • Neutron • Positron – a positive electron • Proton – usually referred to as hydrogen-1 • Any other elemental isotope

Penetrating Ability

Geiger Counter • Used to detect radioactive substances • Units of radiation is the Bacquerel Bq

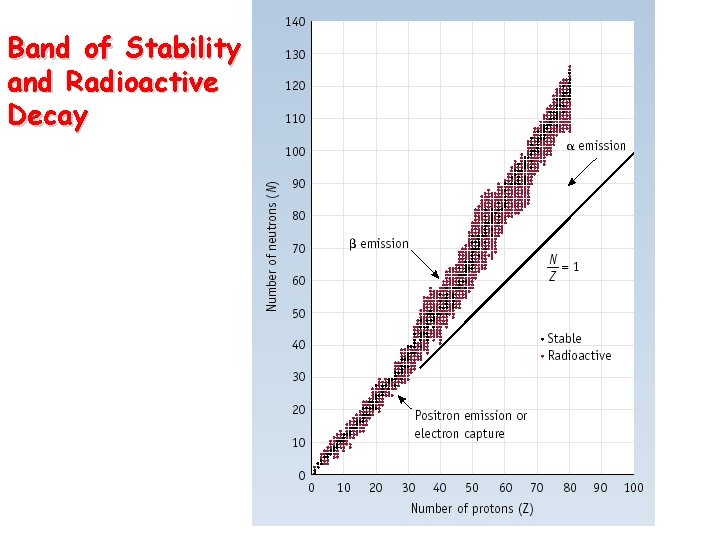
Band of Stability and Radioactive Decay

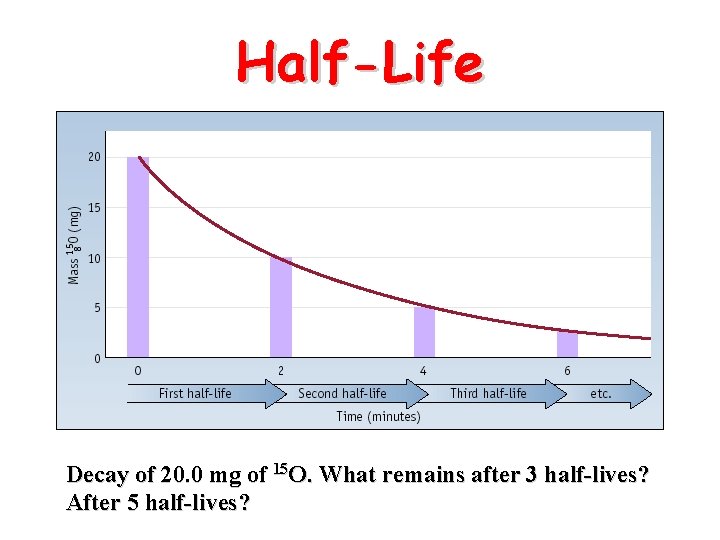
Half-Life • HALF-LIFE is the time that it takes for 1/2 a sample to transmute. • The rate of a nuclear transformation depends only on the “reactant” concentration.

Half-Life Decay of 20. 0 mg of 15 O. What remains after 3 half-lives? After 5 half-lives?

Kinetics of Radioactive Decay For each duration (half-life), one half of the substance decomposes. For example: Ra-234 has a half-life of 3. 6 days If you start with 50 grams of Ra-234 After 3. 6 days > 25 grams After 7. 2 days > 12. 5 grams After 10. 8 days > 6. 25 grams

Kinetics of Radioactive Decay A daughter N = N 0(1/2 )(t / t 1/2 ) Ra-234 has a half-life of 3. 6 days If you start with 50 grams of Ra-234

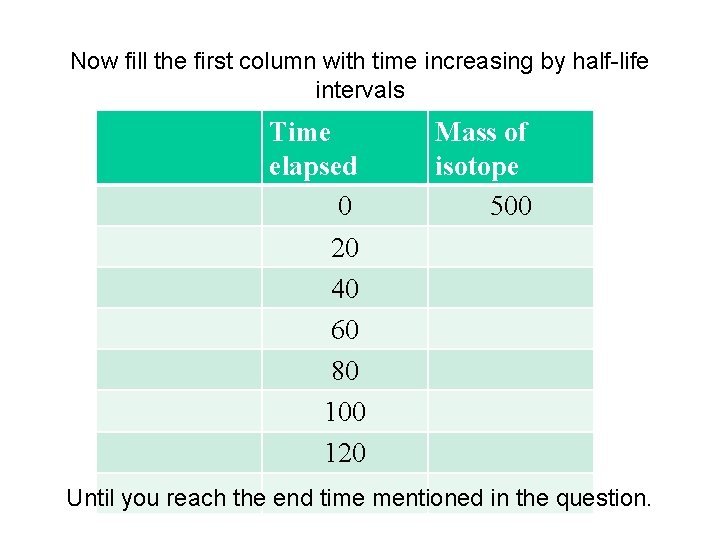
A radioactive substance has a half-life of 20 minutes. If we begin with a 500 g sample, how much of the original sample remains after two hours? Guestimation method Make a table with 2 columns First column time elapsed Second column mass of isotope Time elapsed 0 Mass of isotope 500

Now fill the first column with time increasing by half-life intervals Time elapsed 0 20 40 60 80 100 120 Mass of isotope 500 Until you reach the end time mentioned in the question.

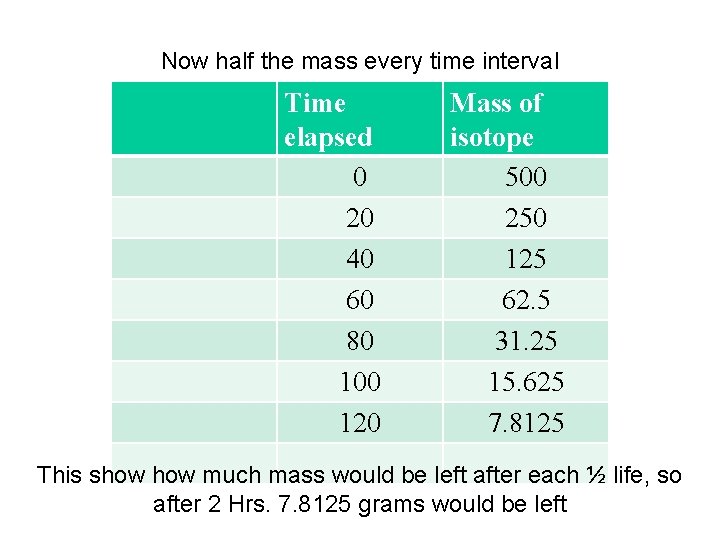
Now half the mass every time interval Time elapsed 0 20 40 60 80 100 120 Mass of isotope 500 250 125 62. 5 31. 25 15. 625 7. 8125 This show much mass would be left after each ½ life, so after 2 Hrs. 7. 8125 grams would be left

The half-life of a material is 2 hours. If the initial count rate is 864 Bq, how long will it take for the count rate to fall to 27 Bq Time elapsed 0 2 4 6 8 10 Mass of isotope 864

The half-life of a material is 3 hours. If the initial count rate is 544 Bq, what will the count rate be after 15 hours? Guestimation method Time 0 Count rate

Radiocarbon Dating 14 N 7 + 01 n 14 C 6 14 N 7 + 11 H + -10 b + n t½ = 5730 years Uranium-238 Dating 238 U 92 206 Pb 82 + 8 24 a + 6 -10 b t½ = 4. 51 x 109 years 23. 3

Learning Check! The half life of I-123 is 13 hr. How much of a 64 mg sample of I-123 is left after 31 hours?