ntrast Modification in Image Data togram Modification Rule

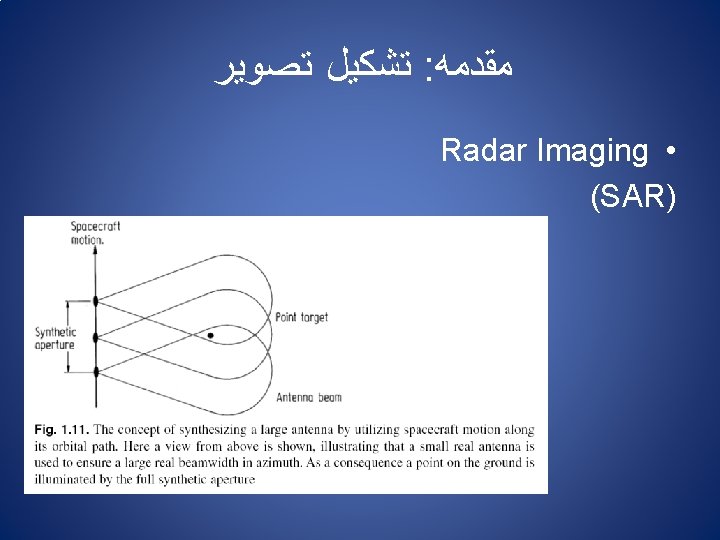
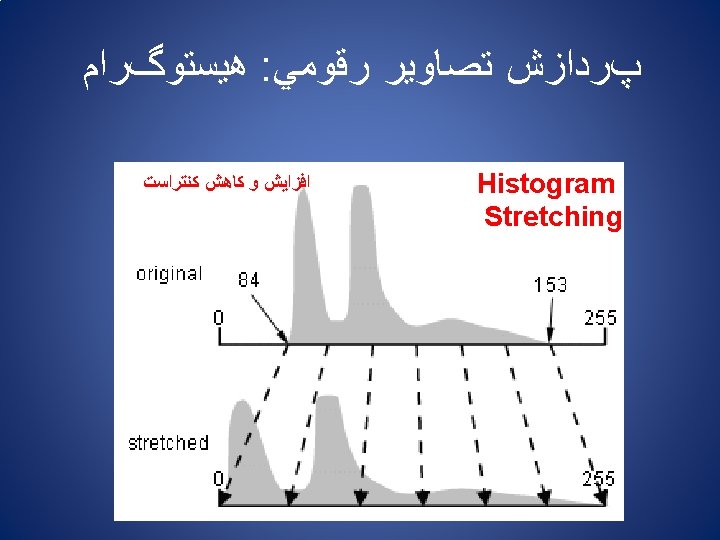
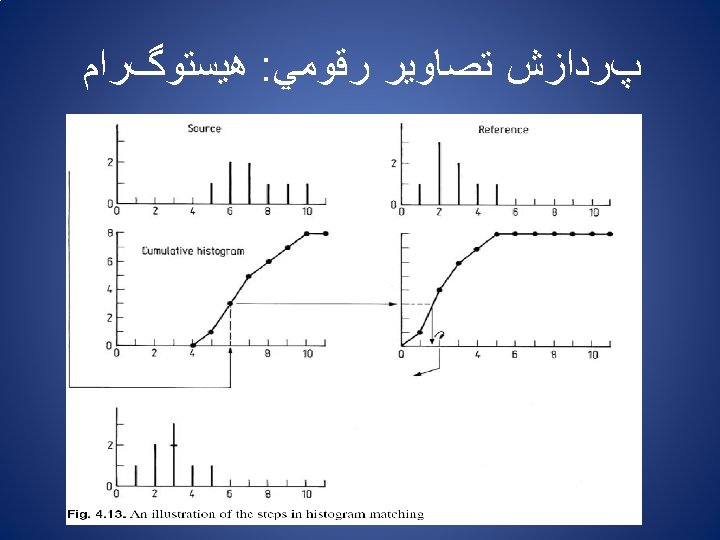
ﻫﻴﺴﺘﻮگﺮﺍﻡ : پﺮﺩﺍﺯﺵ ﺗﺼﺎﻭﻳﺮ ﺭﻗﻮﻣﻲ ntrast Modification in Image Data togram Modification Rule x : the old brightness value of a particular bar in the histogram y : the corresponding new brightness value

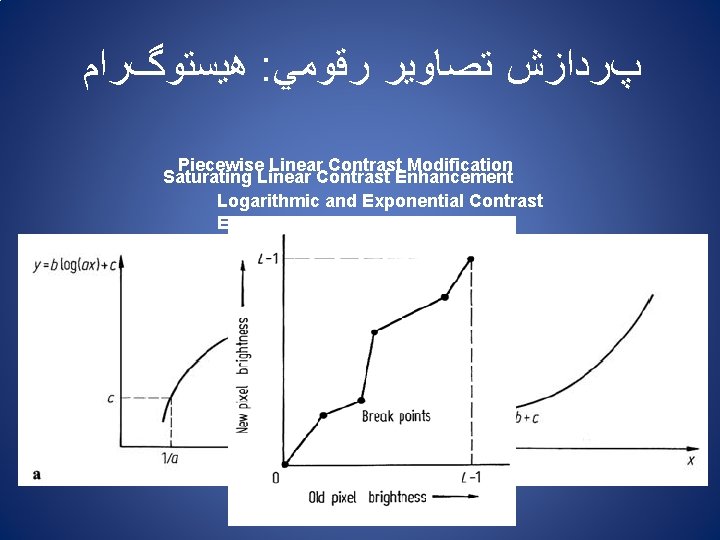
ﻫﻴﺴﺘﻮگﺮﺍﻡ : پﺮﺩﺍﺯﺵ ﺗﺼﺎﻭﻳﺮ ﺭﻗﻮﻣﻲ Piecewise Linear Contrast Modification Saturating Linear Contrast Enhancement Logarithmic and Exponential Contrast Enhancement

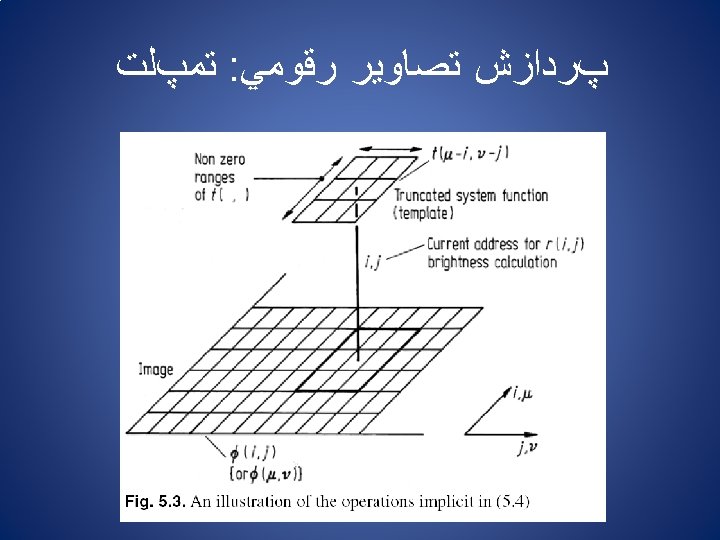
پﺮﺩﺍﺯﺵ ﺗﺼﺎﻭﻳﺮ ﺭﻗﻮﻣﻲ Neighbourhood Operations (Template Operators)

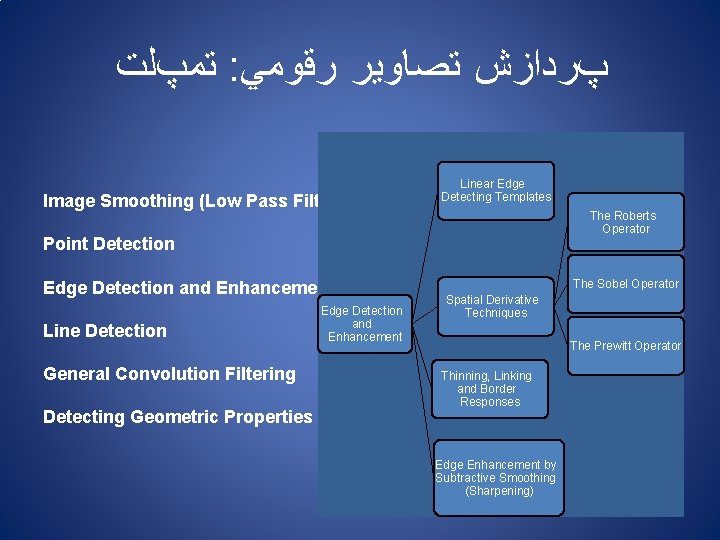
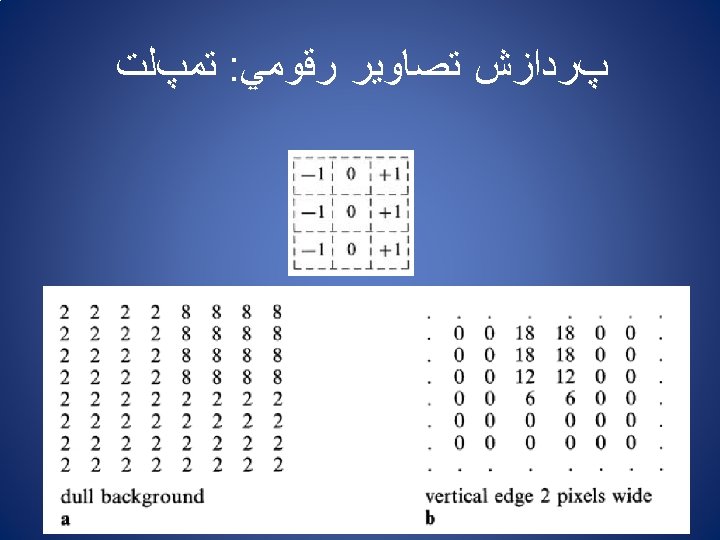
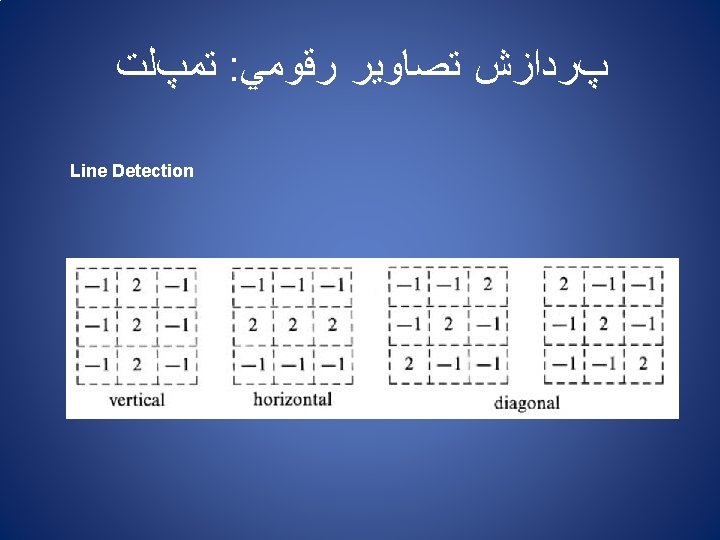
ﺗﻤپﻠﺖ : پﺮﺩﺍﺯﺵ ﺗﺼﺎﻭﻳﺮ ﺭﻗﻮﻣﻲ Image Smoothing (Low Pass Filtering) Linear Edge Mean Value Smoothing Detecting Templates Image Smoothing Point Detection Filtering Edge Detection and Enhancement Line Detection General Convolution Filtering Detecting Geometric Properties The Roberts Median Operator Edge Detection and Enhancement The Sobel Operator Spatial Derivative Techniques The Prewitt Operator Thinning, Linking and Border Responses Edge Enhancement by Subtractive Smoothing (Sharpening)

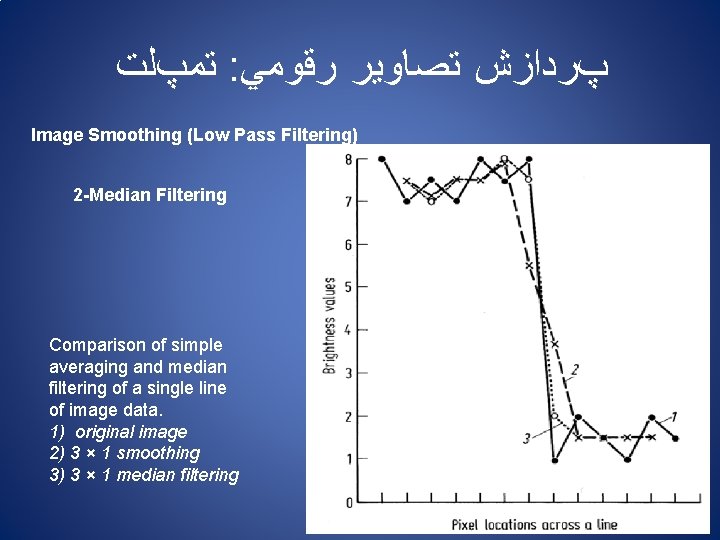
ﺗﻤپﻠﺖ : پﺮﺩﺍﺯﺵ ﺗﺼﺎﻭﻳﺮ ﺭﻗﻮﻣﻲ Image Smoothing (Low Pass Filtering) 1 - Mean Value Smoothing Modified Mean Value Smoothing Edges and Lines be saved Thresho ld

ﺗﻤپﻠﺖ : پﺮﺩﺍﺯﺵ ﺗﺼﺎﻭﻳﺮ ﺭﻗﻮﻣﻲ Illustration of the effect of median filtering on an image which contains impulsive noise. a Original image; b Image with noise; c Filtered image

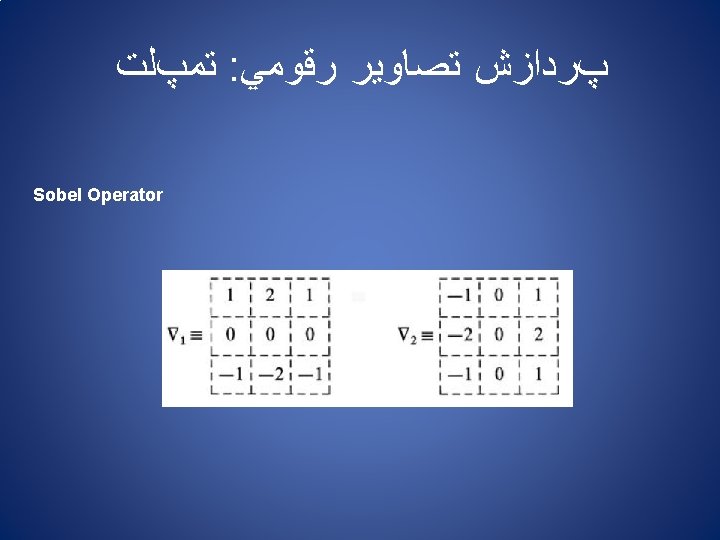
ﺗﻤپﻠﺖ : پﺮﺩﺍﺯﺵ ﺗﺼﺎﻭﻳﺮ ﺭﻗﻮﻣﻲ patial Derivative Techniques Roberts Operator Sobel Operator Response of a the Robert’s operator and b the Sobel

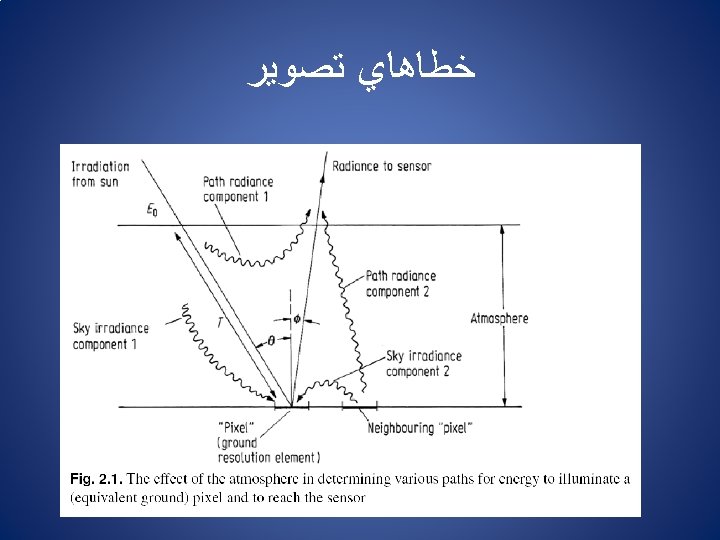
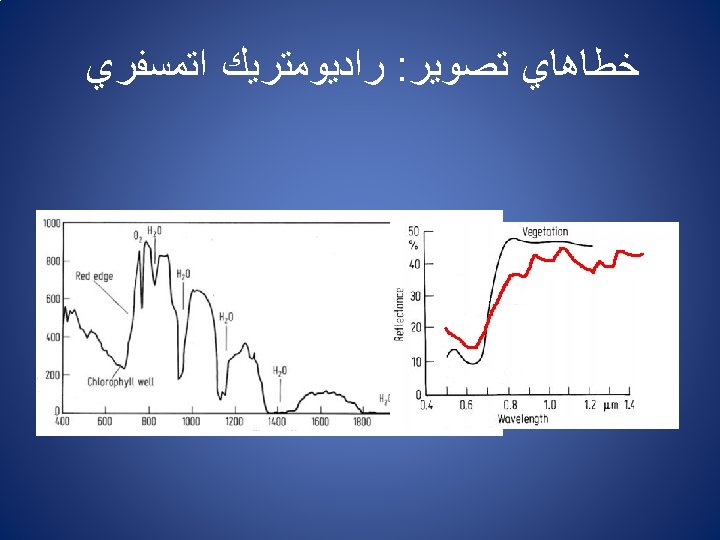
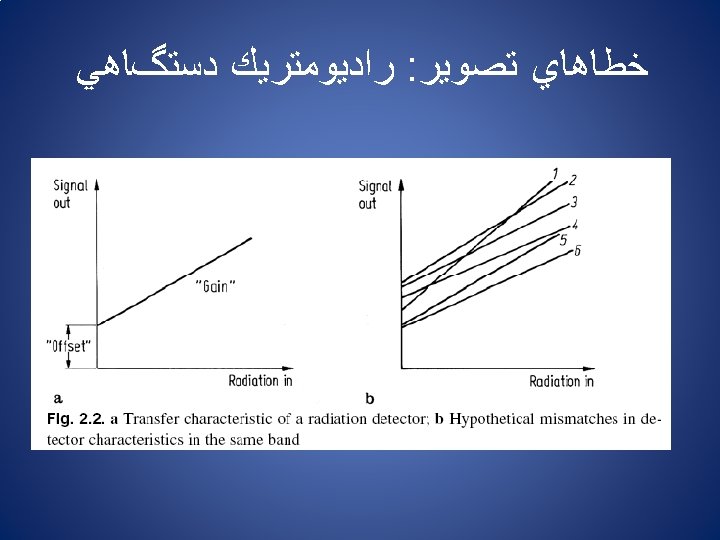
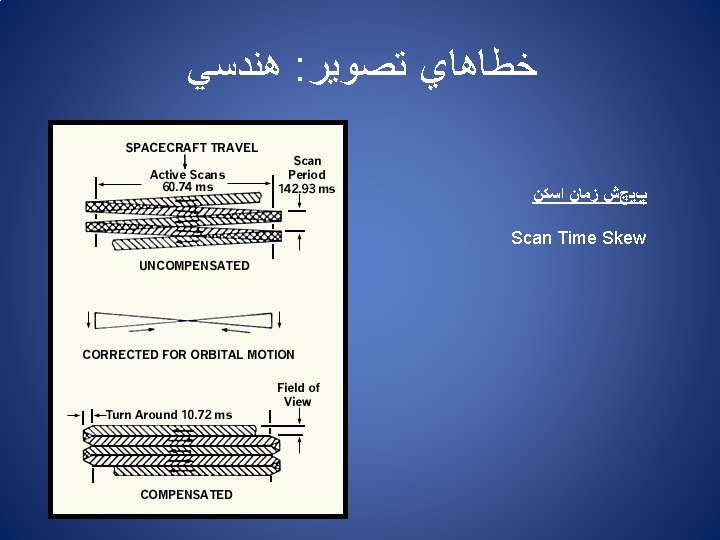
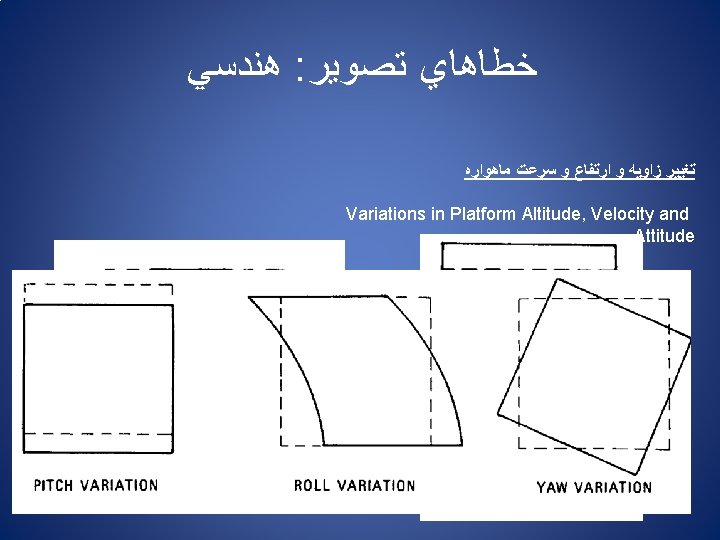
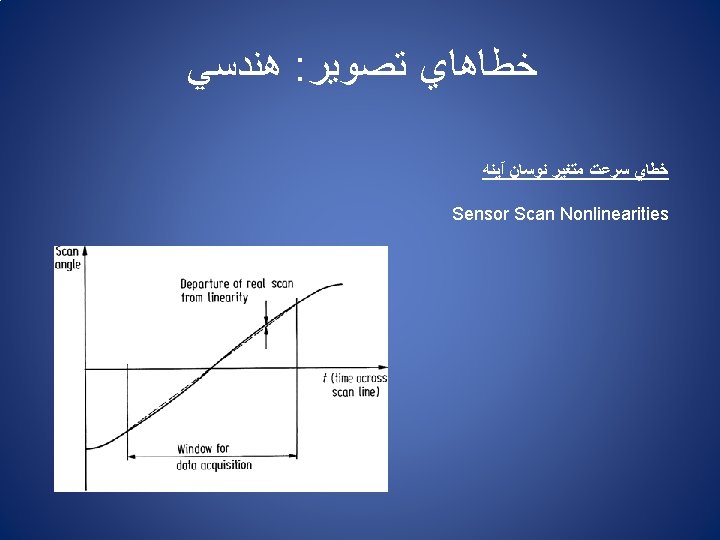
ﻫﻨﺪﺳﻲ : ﺧﻄﺎﻫﺎﻱ ﺗﺼﻮﻳﺮ Sources of Geometric Distortion:

ﻫﻨﺪﺳﻲ : ﺧﻄﺎﻫﺎﻱ ﺗﺼﻮﻳﺮ Image Geo. Referencing, Geo. Coding, Registration ﺗﺼﺤﻴﺢ ﺧﻄﺎﻱ ﻫﻨﺪﺳﻲ ﻓﺘﻮگﺮﺍﻣﺘﺮﻱ. 1 Colinearity • Rational Functions • ﺳﻨﺠﺶ ﺍﺯ ﺩﻭﺭ. 2 Polynomial • Special Functions • Rational o Functions Modified Colinearity o

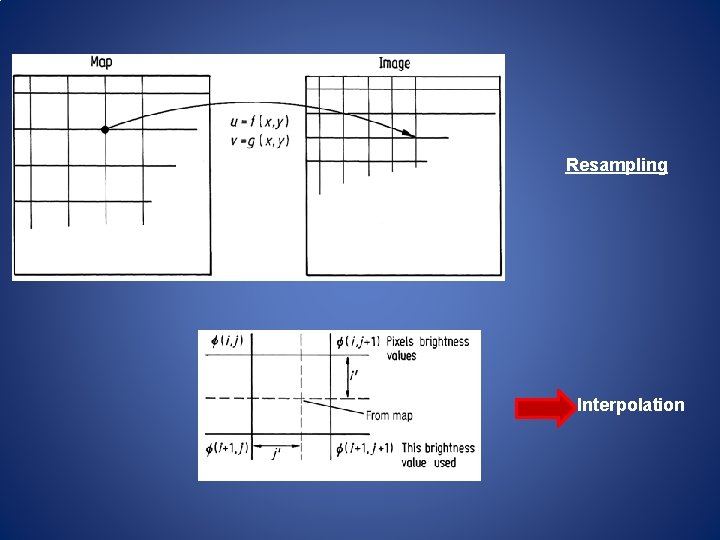
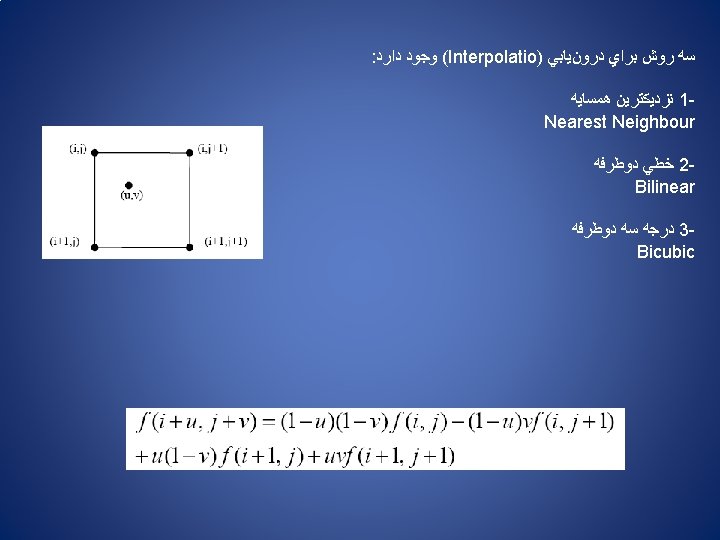
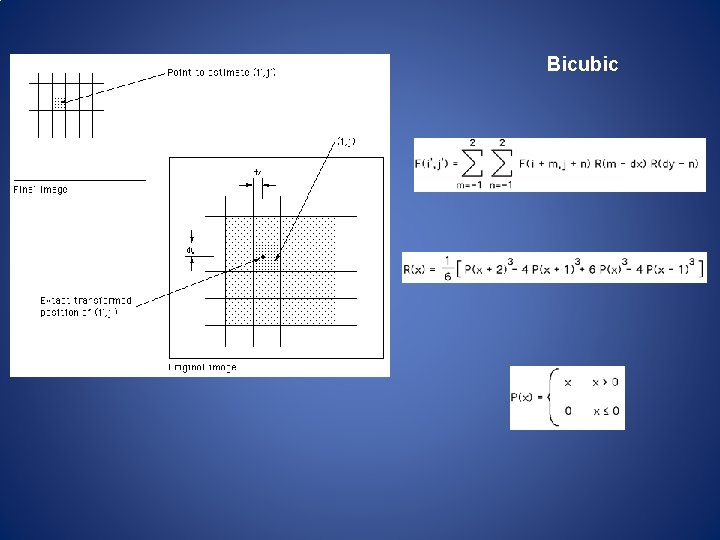
Resampling Interpolation

Bicubic

ﻫﻨﺪﺳﻲ : ﺧﻄﺎﻫﺎﻱ ﺗﺼﻮﻳﺮ Image Registration 1. Georeferencing and Geocoding 2. Image to Image Registration

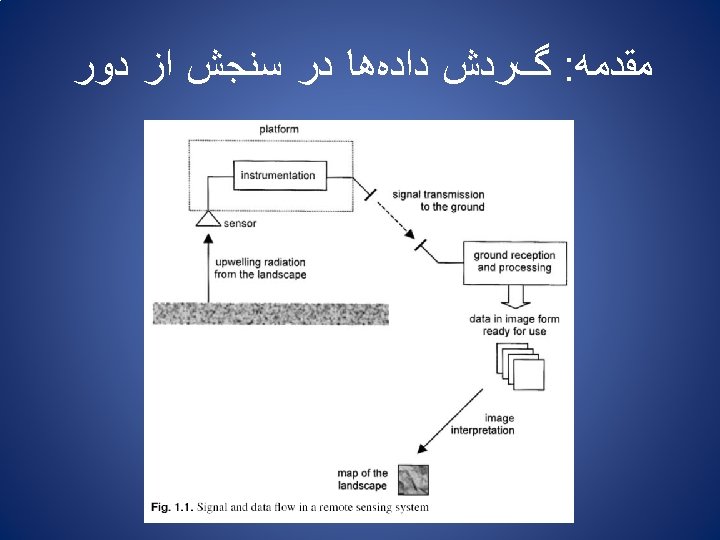
ﻫﻨﺪﺳﻲ : ﺧﻄﺎﻫﺎﻱ ﺗﺼﻮﻳﺮ Geocoding • ﺍﻣﻜﺎﻥ ﺑﻴﺎﻥ آﺪﺭﺱ ﻫﺮ پﻴﻜﺴﻞ ﺑﺎ ﻣﺨﺘﺼﺎﺕ ﺟﻐﺮﺍﻓﻴﺎﻳﻲ Georeferencing • ﺩﻳﺪﻥ ﺗﺼﻮﻳﺮ ﺑﺎﺯﻧﻤﻮﻧﻪﺑﺮﺩﺍﺭﻱ ﺷﺪﻩ ﺩﺭ گﺮﻳﺪ ﻣﺨﺘﺼﺎﺕ ﻧﻘﺸﻪ Geocoding: Expressing image pixel addresses in terms of a map coordinate Georeferencing: Geometrical error calculation/modeling followed by image resampling

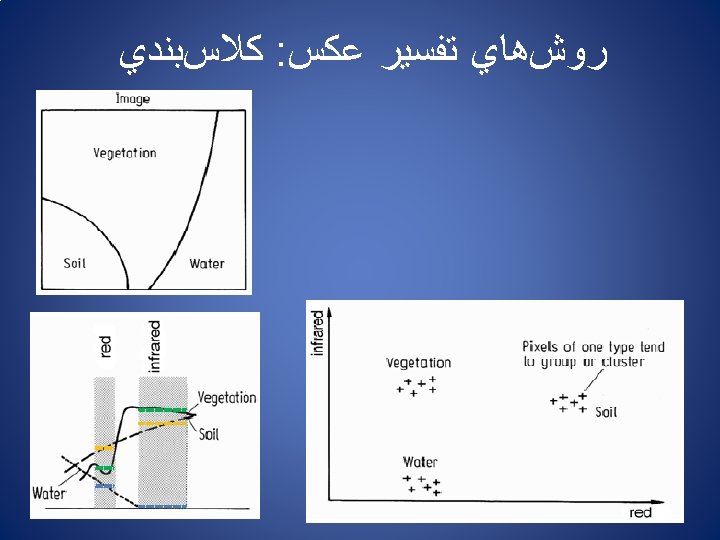
ﺭﻭﺵﻫﺎﻱ ﺗﻔﺴﻴﺮ ﻋﻜﺲ Approaches to Image Interpretation ﺗﻔﺴﻴﺮ Image interpretation ﻋﻜﺴﻲ ﺗﺤﻠﻴﻞ ﻋﺪﺩﻱ Quantitative analysis

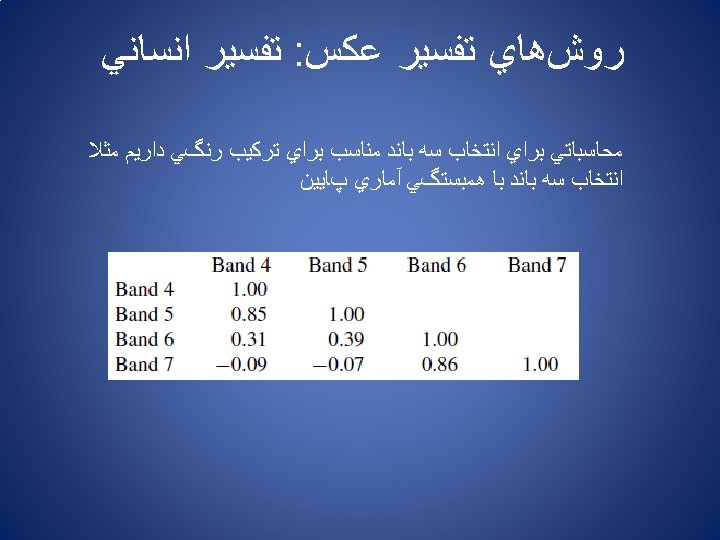
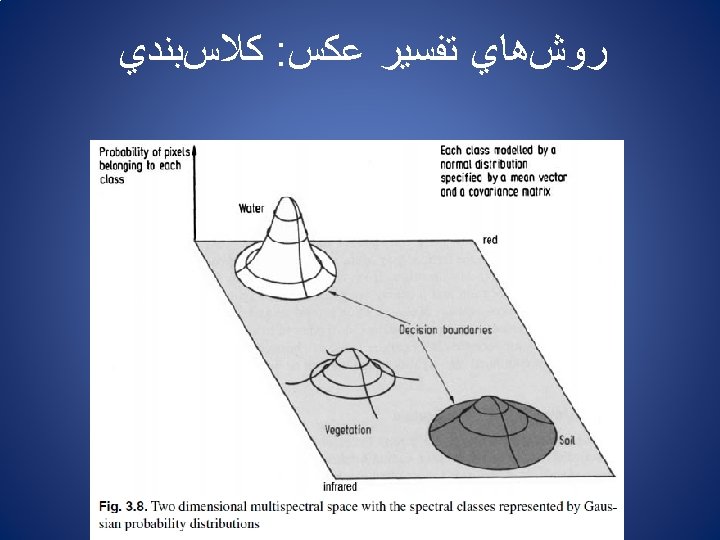
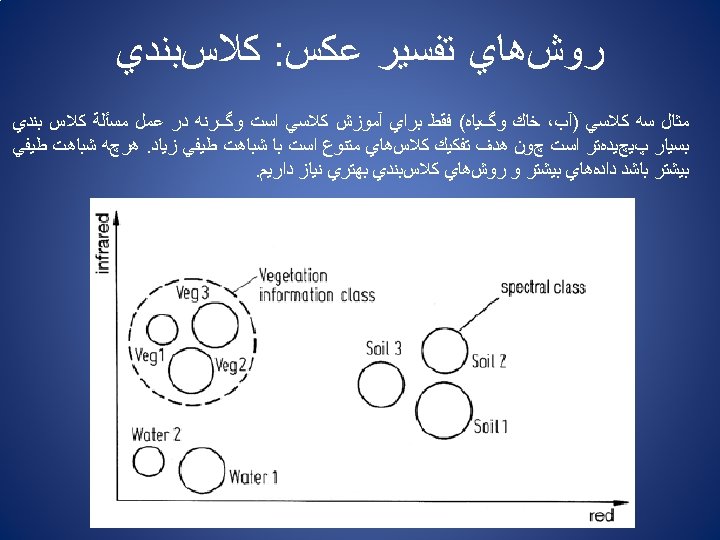
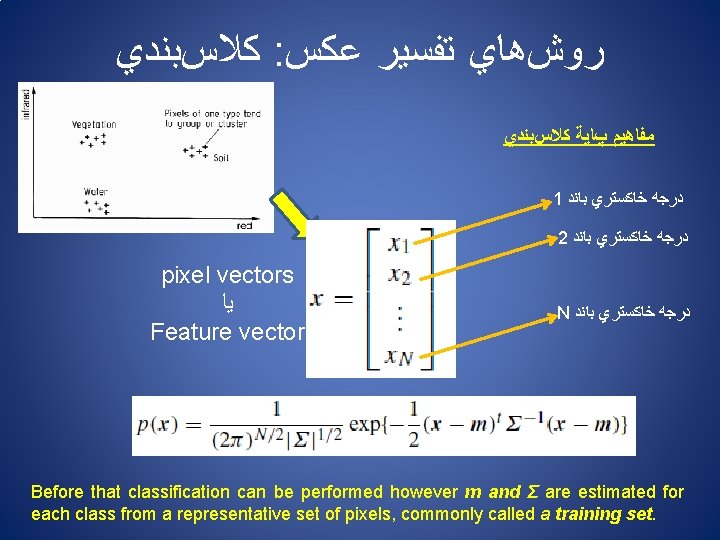
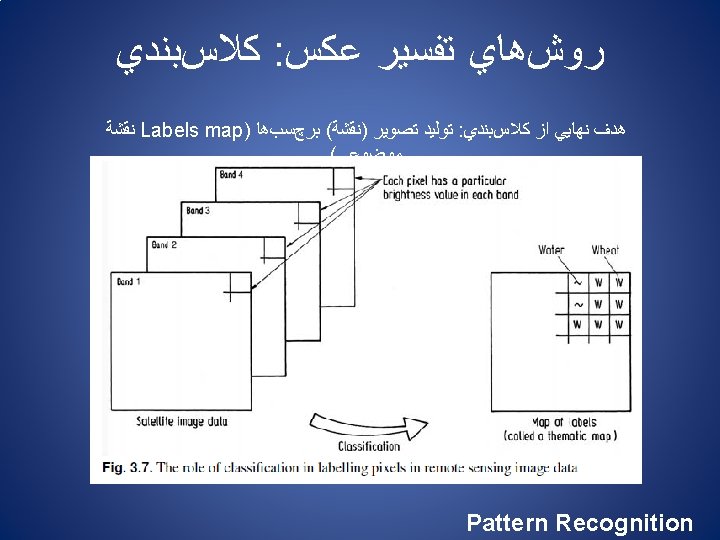
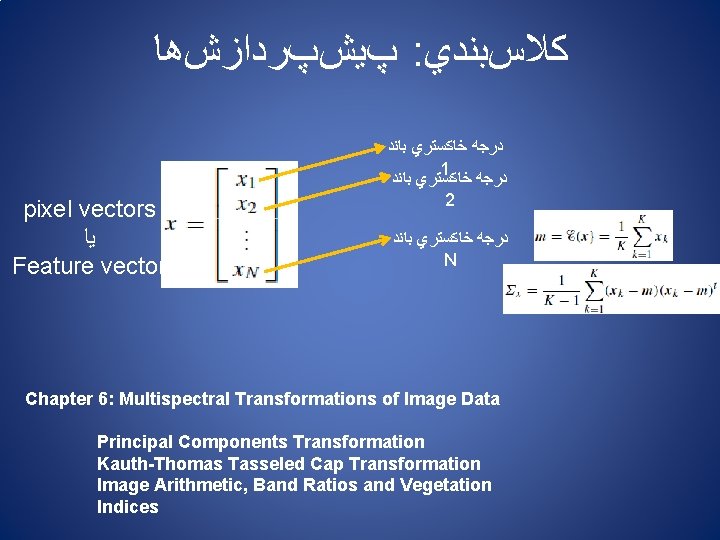
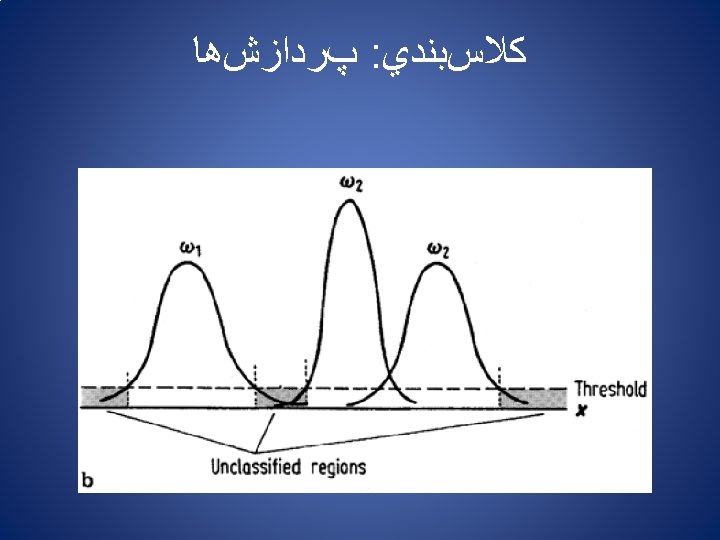
ﻛﻼﺱﺑﻨﺪﻱ : ﺭﻭﺵﻫﺎﻱ ﺗﻔﺴﻴﺮ ﻋﻜﺲ ﻣﻔﺎﻫﻴﻢ پﺎﻳﺔ ﻛﻼﺱﺑﻨﺪﻱ 1 ﺩﺭﺟﻪ ﺧﺎﻛﺴﺘﺮﻱ ﺑﺎﻧﺪ 2 ﺩﺭﺟﻪ ﺧﺎﻛﺴﺘﺮﻱ ﺑﺎﻧﺪ pixel vectors ﻳﺎ Feature vector N ﺩﺭﺟﻪ ﺧﺎﻛﺴﺘﺮﻱ ﺑﺎﻧﺪ Before that classification can be performed however m and Σ are estimated for each class from a representative set of pixels, commonly called a training set.

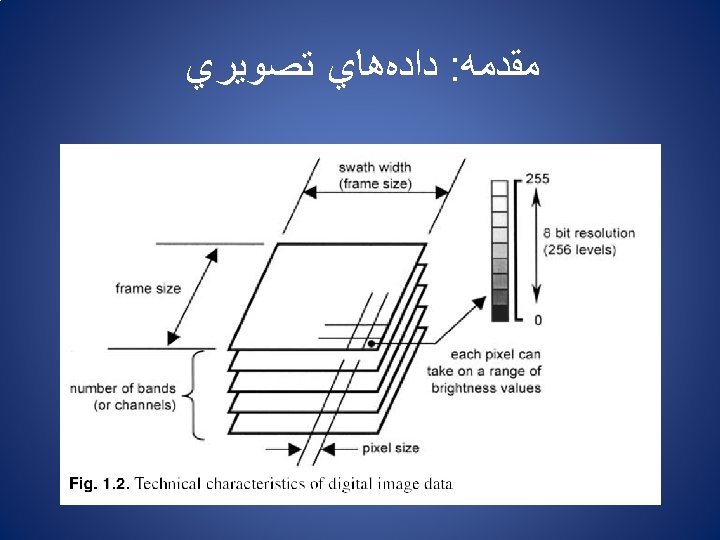
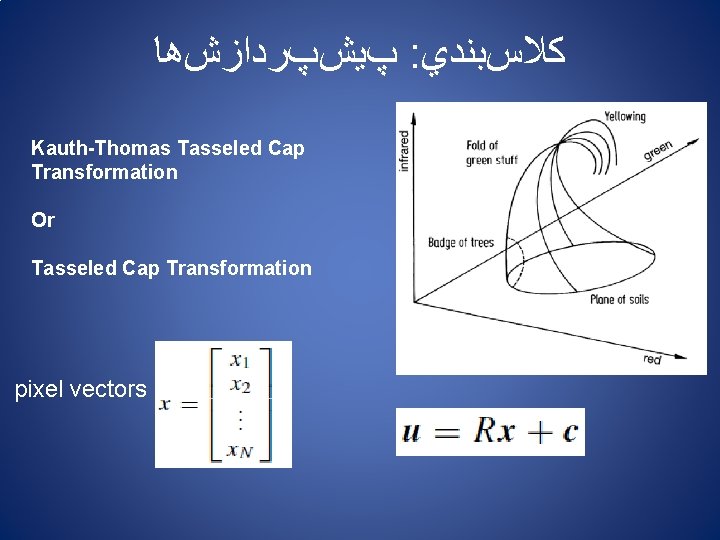
پﻴﺶپﺮﺩﺍﺯﺵﻫﺎ : ﻛﻼﺱﺑﻨﺪﻱ pixel vectors ﻳﺎ Feature vector ﺩﺭﺟﻪ ﺧﺎﻛﺴﺘﺮﻱ ﺑﺎﻧﺪ 1 ﺩﺭﺟﻪ ﺧﺎﻛﺴﺘﺮﻱ ﺑﺎﻧﺪ 2 ﺩﺭﺟﻪ ﺧﺎﻛﺴﺘﺮﻱ ﺑﺎﻧﺪ N Chapter 6: Multispectral Transformations of Image Data Principal Components Transformation Kauth-Thomas Tasseled Cap Transformation Image Arithmetic, Band Ratios and Vegetation Indices

پﻴﺶپﺮﺩﺍﺯﺵﻫﺎ : ﻛﻼﺱﺑﻨﺪﻱ Principal Components Transformation

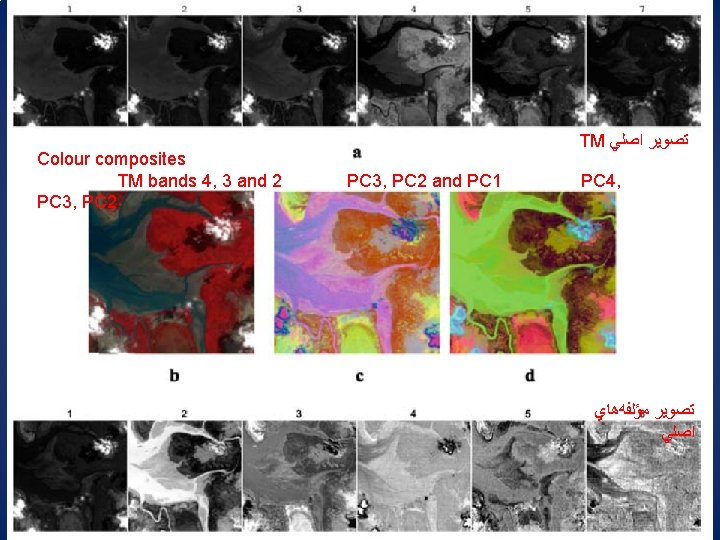
Colour composites TM bands 4, 3 and 2 PC 3, PC 2 TM ﺗﺼﻮﻳﺮ ﺍﺻﻠﻲ PC 3, PC 2 and PC 1 PC 4, ﺗﺼﻮﻳﺮ ﻣﺆﻠﻔﻪﻫﺎﻱ ﺍﺻﻠﻲ

پﻴﺶپﺮﺩﺍﺯﺵﻫﺎ : ﻛﻼﺱﺑﻨﺪﻱ Kauth-Thomas Tasseled Cap Transformation Or Tasseled Cap Transformation pixel vectors

پﺮﺩﺍﺯﺵﻫﺎ : ﻛﻼﺱﺑﻨﺪﻱ Steps in Supervised Classification 1. Decide the set of ground cover types (for example: water, urban regions, croplands, rangelands, etc. ) 2. Choose prototype pixels (training data) from each of the desired classes using site visits, maps, air photographs or even photointerpretation. 3. Use the training data to estimate the parameters of the particular classifier. The set of parameters for a given class is sometimes called the signature of that class. 4. Using the trained classifier, label or classify every pixel in the image into one of the desired ground cover types (information classes). 5. Produce tabular summaries or thematic (class) maps. 6. Assess the accuracy of the final product using a labelled testing data set.

پﺮﺩﺍﺯﺵﻫﺎ : ﻛﻼﺱﺑﻨﺪﻱ Maximum Likelihood Classification Bayes’ Classification

پﺮﺩﺍﺯﺵﻫﺎ : ﻛﻼﺱﺑﻨﺪﻱ Number of Training Pixels Required for Each Class For an N dimensional multispectral space the covariance matrix is symmetric of size N × N. It has, therefore, 1/2 N(N + 1) distinct elements that need to be estimated from the training data. To avoid the matrix being singular at least N(N + 1) independent samples is needed. Fortunately, each N dimensional pixel vector in fact contains N samples (one in each waveband); thus the minimum number of independent training pixels required is (N+1). Because of the difficulty in assuring independence of the pixels, usually many more than this minimum number is selected. Swain and Davis (1978) recommend as a practical minimum that 10 N training pixels per spectral class be used, with as many as 100 N per class if possible.

پﺮﺩﺍﺯﺵﻫﺎ : ﻛﻼﺱﺑﻨﺪﻱ nimum Distance Classification

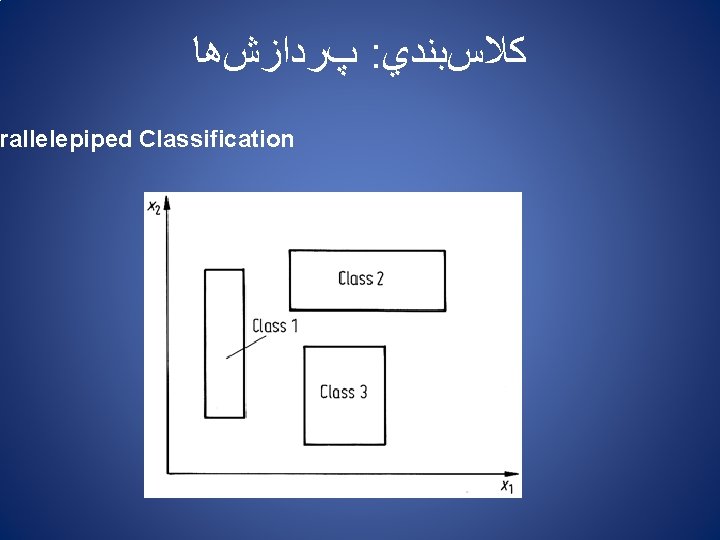
پﺮﺩﺍﺯﺵﻫﺎ : ﻛﻼﺱﺑﻨﺪﻱ rallelepiped Classification

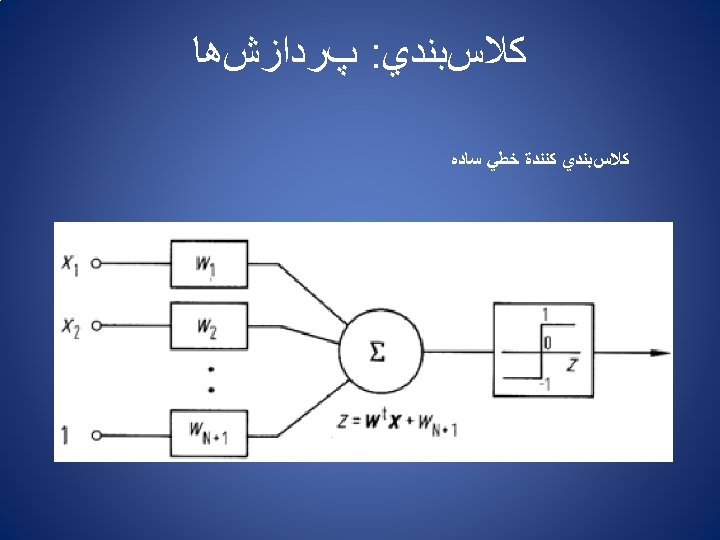
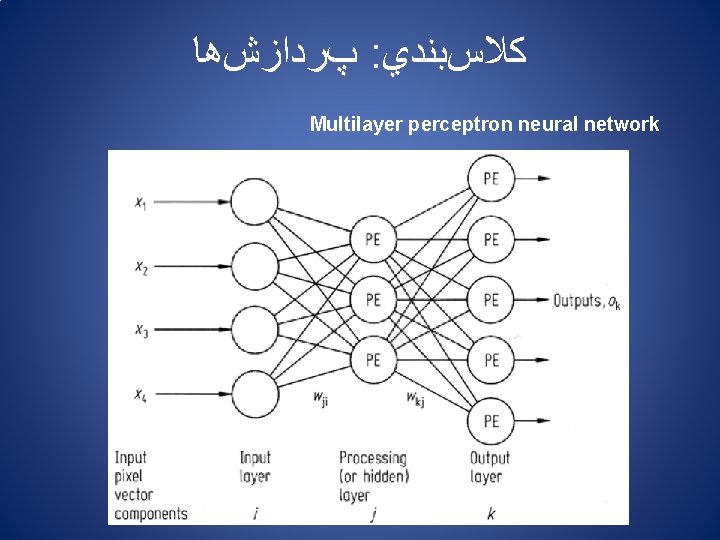
پﺮﺩﺍﺯﺵﻫﺎ : ﻛﻼﺱﺑﻨﺪﻱ Multilayer perceptron neural network

پﺮﺩﺍﺯﺵﻫﺎ : ﻛﻼﺱﺑﻨﺪﻱ ergings and Deletions tting Elongated Clusters