NS Equations in Einstein Notation P M V

N-S Equations in Einstein Notation P M V Subbarao Professor Mechanical Engineering Department I I T Delhi Being Useful to Society at Large……

Einstein Notation : Vector Calculus Gradient of a scalar, T Divergence of a vector Gradient of a vector

Special Notes • To avoid confusion between fixed and repeated indices or different repeated indices, etc, special notes are proposed. • Note 1: No index can be repeated more than twice. • Note 2: Number of free indices shows how many quantities are represented by a single term. • Note 3: If the equation looks like this:

Tensors : Vectors of Second Order • Second order vectors are more complex constructs. The three projections of this tensor, onto coordinate axes are obtained by inner product. These projections are vectors (not scalars!). In array form the three components of a tensor A are vectors denoted by

where each vector i has three components therefore is written in the matrix form

Stress Tensor in Einstein Notation

N-S Equations in Einstein Notation The Navier-Stokes equations, fundamental to the subject of viscousfluid flow. Considerable economy is achieved by rewriting them as a single vector equation, using the indicia 1 notation:

Fluid Mechanics Made Easy • Incompressibility is an excellent point of departure in theory of incompressible viscous flow. • It is essential to remember that it assumes constant viscosity too. • For non-isothermal flows, it may be a rather poor approximation. • This approximation is highly objectionable, particularly for liquids, whose viscosity is often highly temperature-dependent. • For gases, whose viscosity is only moderately temperaturedependent, this is a good approximation • This fails only when compressibility becomes important, i. e. , when v 0.

Incompressible Flow • If the fluid is assumed to be of constant density, divv vanishes due to the continuity equation. • The vexing coefficient disappears from Stoke's law. • NS Equations are not greatly simplified, if the first viscosity is allowed to vary with temperature and pressure. • This leads to assumption of is constant, many terms vanish. • A much simpler Navier-Stokes equation for constant viscosity is

Incompressible NS Equations in Cartesian Coordinate system

Incompressible NS Equations in Cylindrical Coordinate system Navier- Stokes equation in r-direction: Navier- Stokes equation in -direction:

Navier- Stokes equation in z-direction:

The Navier-Stokes Equations : : Thermodynamically Irreversible Flows • In thermodynamics view, these are inherently irreversible flows. • Friction & viscosity are basic culprits of irreversibility. • What if the viscosity is negligible?

Euler Equation of Motion • For the special case of inviscid flow (no viscosity), Replacing the convective by the following vector identity Identify that the convective acceleration is expressed in terms of the gradient of the kinetic energy

Simplification of Body Forces • First rearrange the gravitational acceleration vector by introducing a scalar surface potential z. • The gradient of z has the same direction as the unit vector in – x 3 direction. • Furthermore, it has only one component that points in the negative x 3 -direction. • As a result, we may write.

General Compressible Euler Equation of Motion Thus, the Euler equation of motion assumes the following form: Above equation shows that despite the inviscid flow assumption, fluid flow contains vorticities that are inherent in viscous flows but special in inviscid flows. The vortices cause additional entropy production in inviscid flows. This can be better explained using the first law of thermodynamics.

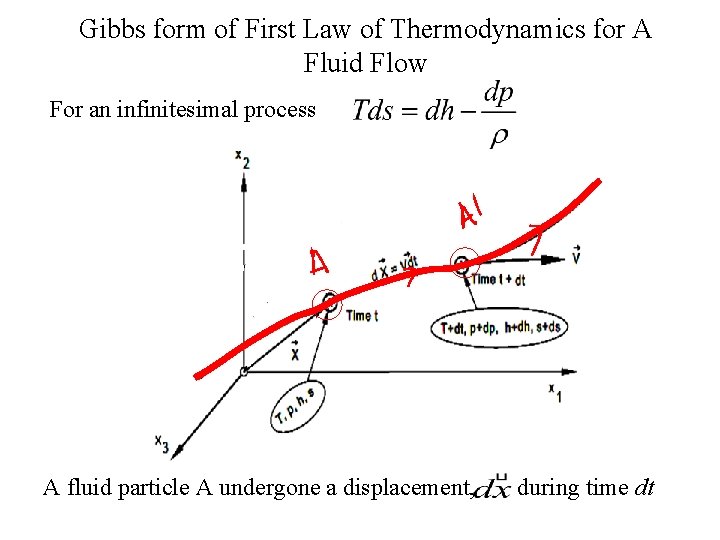
Gibbs form of First Law of Thermodynamics for A Fluid Flow For an infinitesimal process A fluid particle A undergone a displacement, during time dt