NPcompleteness Algorithms and Networks Today Complexity of computational

NP-completeness Algorithms and Networks

Today • Complexity of computational problems • Formal notion of computations • NP-completeness – Why is it relevant? – What is it exactly? – How is it proven? • P vs. NP • Some animals from the complexity zoo 2 Algorithms and Networks: NP-completeness

1 Introduction

Easy problems / Hard problems • Finding the shortest simple path between vertices v and w in a given graph • Determine if there is an Euler tour in a given graph • Testing 2 -colorability • Satisfiability when each clause has two literals 4 • Finding the longest simple path between vertices v and w in a given graph • Determine if there is a Hamiltonian circuit in a given graph • Testing 3 -colorability • Satisfiability when each clause has three literals Algorithms and Networks: NP-completeness

Fast and slow • Algorithms whose running time is polynomial in input size • Algorithms whose running time is exponential in input size • Or worse… Or in between? ? ? 5 Algorithms and Networks: NP-completeness

EXPTIME • Many problems appear not to have a polynomial time algorithm • For a few, we can proof that each algorithm needs exponential time: – EXPTIME hardness, in particular generalized games (Generalized Go, Generalized Chess) • For most, including many important and interesting problems, we cannot. 6 Algorithms and Networks: NP-completeness

NP-completeness • Theory shows relations and explains behavior of many combinatorial problems • From many fields: – – – 7 Logic Graphs, networks, logistics, scheduling Databases Compiler optimization Graphics … Algorithms and Networks: NP-completeness

We need formalisation! • Formal notion of – problem instance – decision problem – computation – running time 8 Algorithms and Networks: NP-completeness

2 Abstract and concrete problems

Different versions of problems • Decision problems – Answer is yes or no Focus on decision problems • Optimization problems – Answer is a number • Construction problems – Answer is some object (set of vertices, function, …) 10 Algorithms and Networks: NP-completeness

Abstract versus concrete problems • Abstract: – Talks about graphs, logic formulas, applications, . . . • Concrete: – Inputs are sets of strings in finite alphabet 11 Algorithms and Networks: NP-completeness

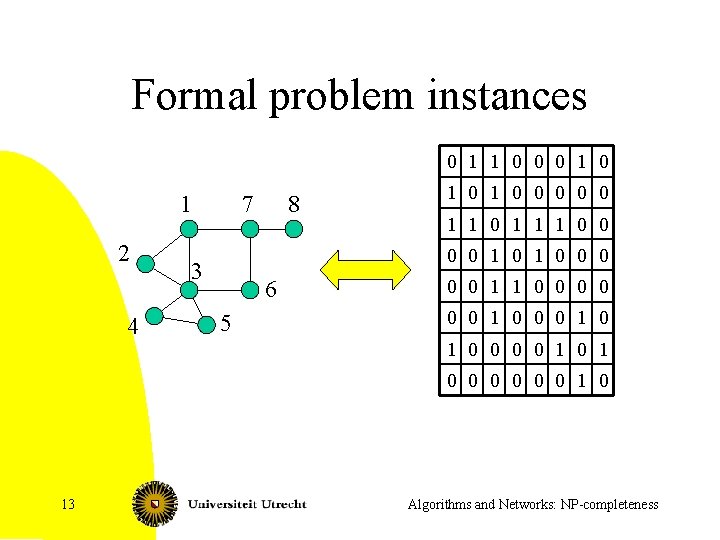
Abstract problem instances • Computers work with bit strings • Problems are described using objects: – G is a graph, … – Given a logic formula, … – Is there a clique of size at least k, . . . • We must map objects to bit strings (or another encoding like Gödel numbers. . . ) 12 Algorithms and Networks: NP-completeness

Formal problem instances 0 1 1 0 0 0 1 2 4 7 8 1 0 0 0 1 1 1 0 0 0 3 6 5 0 0 1 1 0 0 0 1 0 1 0 0 0 0 13 Algorithms and Networks: NP-completeness

Abstract decision problems • Abstract decision problem: – Set of instances I • Objects like graphs, integers, logic formulas, etc. – Subset of I: instances where the answer to the problem is YES. 14 Algorithms and Networks: NP-completeness

Encoding / concrete problem • Encoding: mapping of set of instances I to bitstrings in {0, 1}* • Concrete (decision) problem: – Subset of {0, 1}* • With encoding, an abstract decision problem maps to a concrete decision problem 15 Algorithms and Networks: NP-completeness

3 P and NP

Complexity Class P FORMAL • Class of languages L, for which there exists a deterministic Turing Machine deciding whether i L, using running time O(p(|i|)) for some polynomial p 17 INFORMAL • Class of decision problems that have polynomial time algorithms solving them Algorithms and Networks: NP-completeness

P • An algorithm solves a problem – Decides if string in {0, 1}* belongs to subset • Time: deterministic, worst case • Algorithm uses polynomial time, if there is a polynomial p such that on inputs of length n the algorithm uses at most p(n) time. – Size of input x is denoted |x|. • P is the class of decision problems that have an algorithm that solves it in polynomial time 18 Algorithms and Networks: NP-completeness

Using P for abstract problems • Abstract problem (with encoding) is in P, if the resulting problem is in P • In practice: encoding and corresponding concrete problem is assumed very implicitly • For polynomiality, encoding does not matter! – If we can transform encodings in polynomial time to each other • Details: see e. g. , chapter 34 of Introduction to Algorithms 19 Algorithms and Networks: NP-completeness

Language of a problem • Decision problem as a language: – Set of all yes-instances • P is the set of all languages that have a polynomial time decision algorithm 20 Algorithms and Networks: NP-completeness

Verification algorithm • Verification algorithm has two arguments: – Problem input – Certificate (“solution”) • Answers “yes” or “no” • Checks if 2 nd argument is certificate for first argument for studied problem • The language verified by the verification algorithm A is – {i | there is an c with A(i, c)= true} 21 Algorithms and Networks: NP-completeness

Complexity Class NP Two equivalent definitions of NP • Class of languages L, for which there exists a Non-Deterministic Turing Machine deciding whether i L, using running time O(p(|i|)) • Class of languages L, for which there exists a Deterministic Turing Machine verifying whether i L, using a polynomial sized certificate c, and using running time O(p(|i|)) – 22 This definition we use: details follow Algorithms and Networks: NP-completeness

NP • Problems with polynomial time verification algorithm and polynomial size certificates • Problem L belongs to the class NP, if there exists a 2 -argument algorithm A, with – A runs in polynomial time – There is a constant d such that for each i, i is a yesinstance to L, if and only if there is a certificate c with • A(i, c) = true • |c| = O(|i|d) 23 Algorithms and Networks: NP-completeness

Many problems are in NP • Examples: Hamiltonian Path, Maximum Independent Set, Satisfiability, Vertex Cover, … • Al of these have trivial certificates (set of vertices, truth assignment, …) • In NP (not trivial): Integer Linear Program 24 Algorithms and Networks: NP-completeness

P Í NP • If A decides L in polynomial time, then as verification algorithm, compute – B(i, c) = A(i) – “We do not need a certificate”. • Famous open problem: P = NP ? ? Or not? ? 25 Algorithms and Networks: NP-completeness

4 Reducibility

Reducibility • Language L 1 is polynomial time reducible to language L 2 (or: L 1 £P L 2 ), if there exists a polynomial time computable function f : {0, 1}* ® {0, 1}* such that – For all x {0, 1}*: • x L 1 if and only if f(x) L 2 27 Algorithms and Networks: NP-completeness

Lemma: If L 1 £P L 2 then if L 2 Î P, then L 1 Î P. Proof-idea: run an algorithm for L 2 on f(i) for input i to problem L 1. Also: If L 1 £P L 2 then if L 2 NP, then L 1 NP. 28 Algorithms and Networks: NP-completeness

5 NP-completeness and the Cook-Levin theorem

NP-completeness A language L is NP-complete, if 1. L NP 2. For every L’ NP: L’ £P L A language L is NP-hard, if 1. For every L’ NP: L’ £P L • 30 NP-hardness sometimes also used as term for problems that are not a decision problem, and for problems that are ‘harder than NP’ Algorithms and Networks: NP-completeness

What does it mean to be NP-complete? • Evidence that it is (very probably) hard to find an algorithm that solves the problem – Always – Exact – In polynomial time 31 Algorithms and Networks: NP-completeness

CNF-Satisfiability • Given: expression over Boolean variables in conjunctive normal form • Question: Is the expression satisfiable? (Can we give each variable a value true or false such that the expression becomes true). – CNF: “and” of clauses; each clause “or” of variables or negations (xi or not(xj)) 32 Algorithms and Networks: NP-completeness

Cook-Levin theorem • Satisfiability is NP-complete – Most well known is Cook’s proof, using Turing machine characterization of NP. 33 Algorithms and Networks: NP-completeness

Brief sketch of ideas in proof of Cook-Levin theorem • Suppose problem Q is in NP • Build a Turing Machine that – gets on an input tape a string (i, c), with c a certificate of size O(|i|d) – Runs the verification algorithm A in O(|i|q) time – d, q constants • Make a logic formula that expresses “A halts in an accepting state on (i, c)” – Variables: • a(t, r, s): true if at time t, the r’s symbol on the tape is symbol s • b(t, a): true if the machine is at time t at state a • c(t, r): true if at time t, the reading head at the tape is at position r – Lots of clauses that express that the variable act like a Turing Machine tells them to do 34 Algorithms and Networks: NP-completeness

5 Proving that problems are NP-complete

Proving problems NP-complete Lemma 1. Let L’ £P L and let L’ be NP-complete. Then L is NP-hard. 2. Let L’ £P L and let L’ be NP-complete, and L NP. Then L is NP-complete. 36 Algorithms and Networks: NP-completeness

3 -Sat • 3 -Sat is the special case of CNF-Satisfiability where each clause has exactly three literals • Lemma: CNF-Satisfiability £P 3 -Sat – Clauses with one or two literals: • Use two extra variables p and q • Replace 2 -literal clause (x or y) by (x or y or p) and (x or y or not(p)) • Similarly, replace 1 -literal clause by 4 clauses – Clauses with more than three literals: • Repeat until no such clauses – For (l 1 or l 2 or … lr) add new variable t and take as replacement clauses (l 1 or l 2 or t) and (not(t) or l 3 or … or lr) 37 Algorithms and Networks: NP-completeness

3 -Sat is NP-complete • Membership in NP • Reduction – 3 -Sat is important starting problem for many NP-completeness proofs 38 Algorithms and Networks: NP-completeness

Clique • Given: graph G=(V, E), integer k • Question: does G have a clique with at least k vertices? Clique is NP-complete. In NP … easy! NP-hardness: using 3 -sat. 39 Algorithms and Networks: NP-completeness

Reduction for Clique Clause: {x 1, not(x 2), x 3} • One vertex per literal x 1 not(x 2) x 3 per clause • Edges between x 1 vertices in different … clauses, except edges x 2 between xi and not(xi) not(x 3) • If m clauses, look for Clause: {x 1, x 2, not(x 3)} clique of size m 40 Algorithms and Networks: NP-completeness

Correctness • There is a satisfying truth assignment, if and only if there is a clique with m vertices • =>: Select from each clause the true literal. The corresponding vertices form a clique with m vertices. • <=: Set variable xi to true, if a vertex representing xi is in the clique, otherwise set it to false. This is a satisfying truth assignment: – The clique must contain one vertex from each 3 vertices representing a clause. – It cannot contain a vertex representing xi and a vertex representing not(xi). 41 Algorithms and Networks: NP-completeness

Independent set • Independent set: set of vertices W Í V, such that for all v, w W: {v, w} Ï E. • Independent set problem: – Given: graph G, integer k – Question: Does G have an independent set of size at least k? • Independent set is NP-complete 42 Algorithms and Networks: NP-completeness

Independent set is NP-complete • In NP. • NP-hard: transform from Clique. • W is a clique in G, if and only if W is an independent set in the complement of G (there is an edge in Gc iff. there is no edge in G). 43 Algorithms and Networks: NP-completeness

How do I write down this proof? • Theorem. Independent Set is NP-complete. • Proof: The problem belongs to NP: as certificates, we use sets of vertices; we can check in polynomial time for a set that it is a clique, and that its size is at least k. To show NP-hardness, we use a reduction from Clique. Let (G, k) be an input to the clique problem. Transform this to (Gc, k) with Gc the complement of G. As G has a clique with at least k vertices, if and only if Gc has an independent set with k vertices, this is a correct transformation. The transformation can clearly be carried out in polynomial time. QED 44 Algorithms and Networks: NP-completeness

Writing an NP-completeness proof • State theorem • Proof starts (or ends) with showing that problem belongs to NP. – Sometimes (e. g. , in journal paper: trivial). Only if it is. – Otherwise, explain the certificates and how / that they can be checked in polynomial time • State which known NP-complete problem you transform from – Careful: do not go in the wrong direction • Explain the transformation • Give the proof: input to original problem is Yes-instance, if and only if transformed input is Yes-input for known NP-complete problem – Note: you need to proof this in two directions • Phrase: transformation can be carried out in polynomial time, hence problem is NP-complete QED 45 Algorithms and Networks: NP-completeness

Vertex Cover • Set of vertices W Í V with for all {x, y} E: x W or y W. • Vertex Cover problem: – Given G, find vertex cover of minimum size = vertex cover 46 Algorithms and Networks: NP-completeness

Vertex cover is NP-complete • In NP. • NP-hard: transform from independent set. • W is a vertex cover in G, if and only if V-W is an independent set in G. 47 Algorithms and Networks: NP-completeness

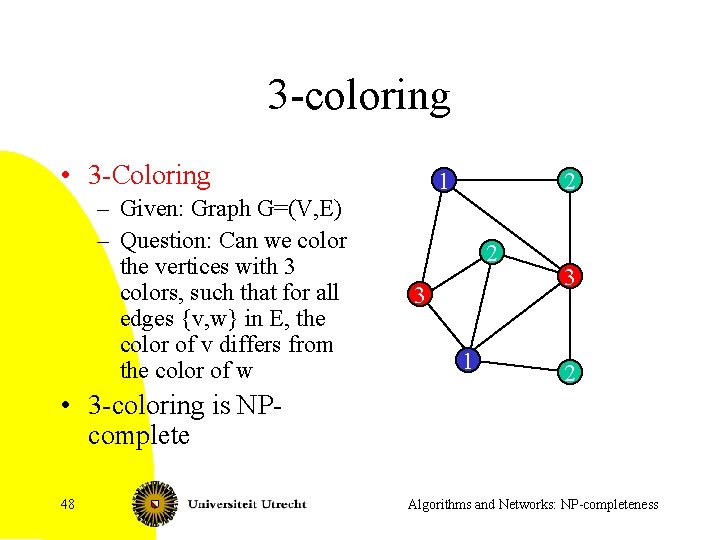
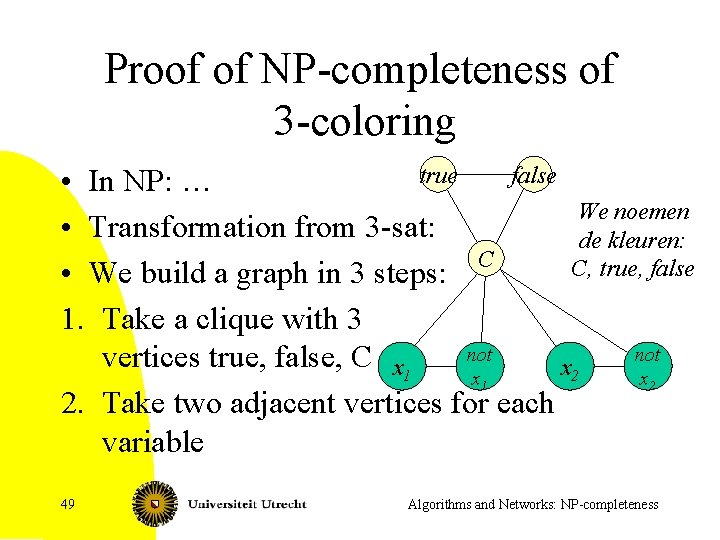
3 -coloring • 3 -Coloring – Given: Graph G=(V, E) – Question: Can we color the vertices with 3 colors, such that for all edges {v, w} in E, the color of v differs from the color of w 1 2 2 3 1 3 2 • 3 -coloring is NPcomplete 48 Algorithms and Networks: NP-completeness

Proof of NP-completeness of 3 -coloring true false • In NP: … We noemen • Transformation from 3 -sat: de kleuren: C C, true, false • We build a graph in 3 steps: 1. Take a clique with 3 not vertices true, false, C x 1 x 2 2. Take two adjacent vertices for each variable 49 Algorithms and Networks: NP-completeness

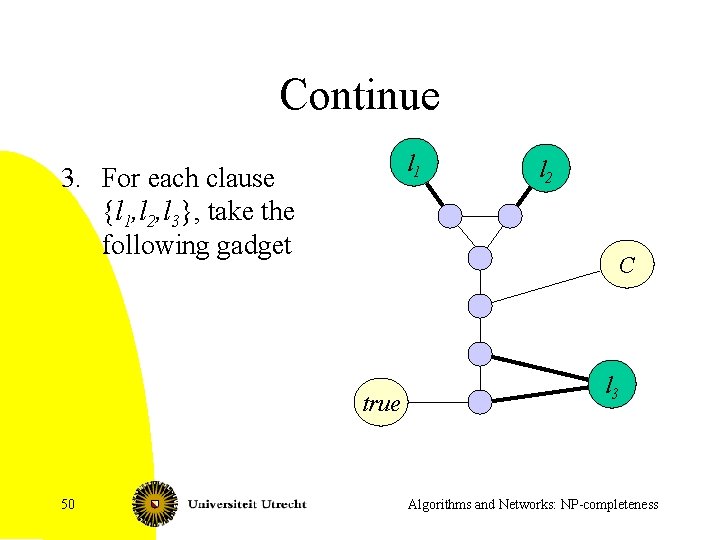
Continue l 1 3. For each clause {l 1, l 2, l 3}, take the following gadget C true 50 l 2 l 3 Algorithms and Networks: NP-completeness

Finish • One can show: • If the formula is satisfiable, then there is a 3 coloring of G • If there is a 3 -coloring of G, then the formula is satisfiable • In both cases, the intuition is a literal vertex is colored true, iff we take it to be true in the formula • … argue transformation takes polynomial time; QED 51 Algorithms and Networks: NP-completeness

6 Three techniques for NPcompleteness proofs Algorithms and Networks: NP-completeness

Techniques for proving NP-hardness 1) Local replacement 2) Restriction 3) Component Design 53 Algorithms and Networks: NP-completeness

6. 1 Local replacement proofs

Technique 1: Local replacement • Form an instance of our problem by – Taking an instance of a known NP-complete problem – Making some change “everywhere” – Such that we get an equivalent instance, but now of the problem we want to show NP-hard 55 Algorithms and Networks: NP-completeness

Examples of Local Replacement • We saw or will see: – 3 -Satisfiability – Independent Set – TSP – Vertex Cover 56 Algorithms and Networks: NP-completeness

Example Local Replacement • Planar 3 -coloring – Given: Planar graph G=(V, E) – Question: Can we color the vertices of G with 3 colors, such that adjacent vertices have different colors? • Plan: transform from 3 -coloring – – 57 Take arbitrary graph G Draw G on the plane So, we possibly get some crossings Replace the crossings by something clever Algorithms and Networks: NP-completeness

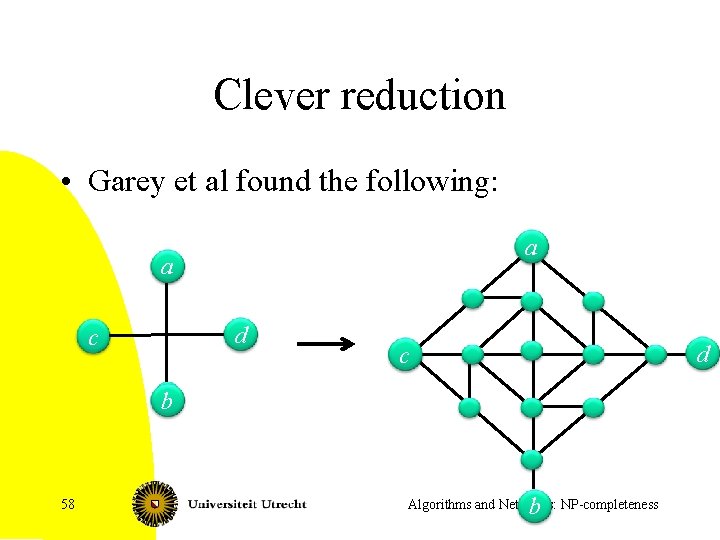
Clever reduction • Garey et al found the following: a a d c b 58 b Algorithms and Networks: NP-completeness

Property of the gadget • If a and b have the same color, we cannot color the gadget with 3 colors • If c and d have the same color, we cannot color the gadget with 3 colors • Otherwise, we can • . . . Some additional details (basically, repeat the step) when an edge has more than one crossing … 59 Algorithms and Networks: NP-completeness

7 Restriction proofs

Technique 2: Restriction • Take the problem. • Add a restriction to the set of instances. NOT to the problem definition! • Show that this is a known NP-complete problem 61 Algorithms and Networks: NP-completeness

Restriction: Weighted Vertex Cover • Weighted vertex cover – Given: Graph G=(V, E), for each vertex v V, a positive integer weight w(v), integer k. – Question: Does G have a vertex cover of total weight at most k? • NP-complete – In NP. – NP-hardness: set all weights to 1 (VC). 62 Algorithms and Networks: NP-completeness

Restriction: Knapsack • Knapsack – Given: Set S of items, each with integer value v and integer weight w, integers W and V. – Question: is there a subset of S of weight no more than W, with total value at least V? • NP-complete – In NP – NP-hardness: set all weights equal to their values (Subset sum) 63 Algorithms and Networks: NP-completeness

9 Component design proofs

Technique 3: Component design • Build (often complicated) parts of an instance with certain properties • Glue them together in such a way that the proof works • Examples: Clique, Hamiltonian Circuit 65 Algorithms and Networks: NP-completeness

Hamiltonian circuit • Given: Graph G • Question: does G have a simple cycle that contains all vertices? 66 Algorithms and Networks: NP-completeness

NP-completeness of Hamiltonian Circuit • HC is in NP. • Vertex Cover £P Hamiltonain Circuit: complicated proof (component design) – Widgets – Selector vertices – Given a graph G and an integer k, we construct a graph H, such that H has a HC, if and only if G has a VC of size k. 67 Algorithms and Networks: NP-completeness

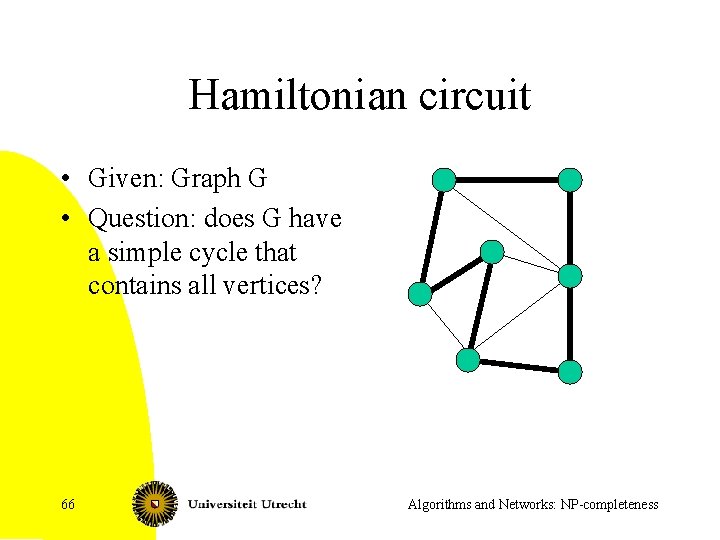
Widget • For each edge {u, v} [u, v, 1] we have a widget Wuv [v, u, 1] [u, v, 6] [v, u, 6] 68 Algorithms and Networks: NP-completeness

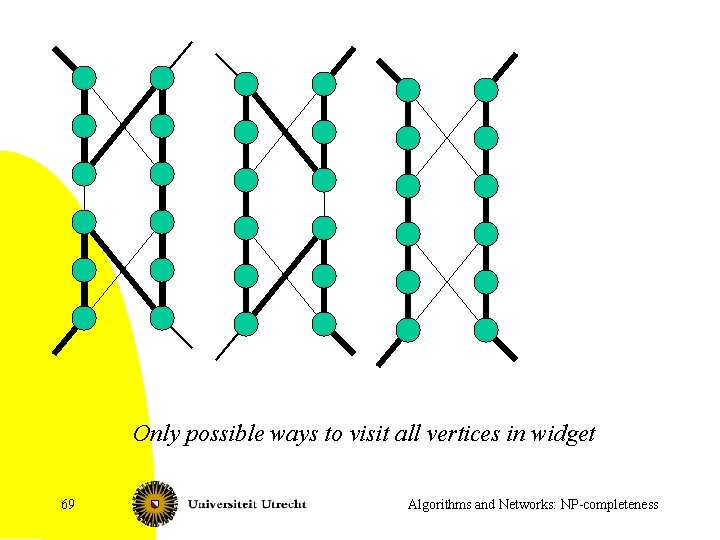
Only possible ways to visit all vertices in widget 69 Algorithms and Networks: NP-completeness

Selector vertices • We have k selector vertices s 1, …, sk • These will represent the vertices selected for the vertex cover 70 Algorithms and Networks: NP-completeness

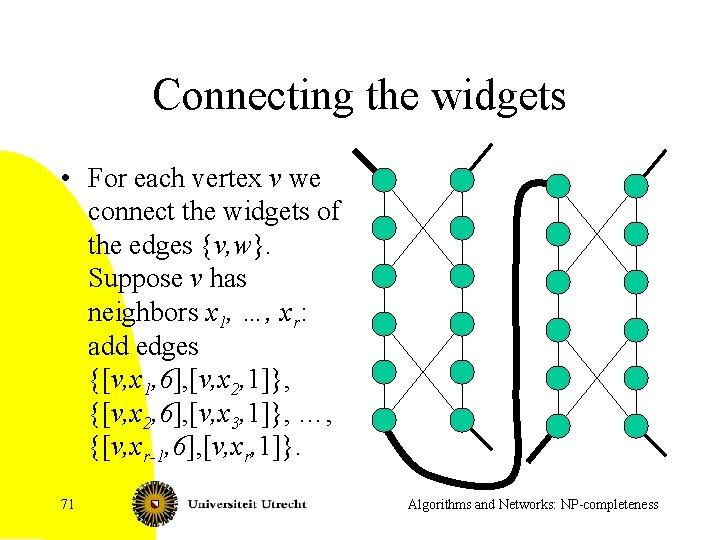
Connecting the widgets • For each vertex v we connect the widgets of the edges {v, w}. Suppose v has neighbors x 1, …, xr: add edges {[v, x 1, 6], [v, x 2, 1]}, {[v, x 2, 6], [v, x 3, 1]}, …, {[v, xr-1, 6], [v, xr, 1]}. 71 Algorithms and Networks: NP-completeness

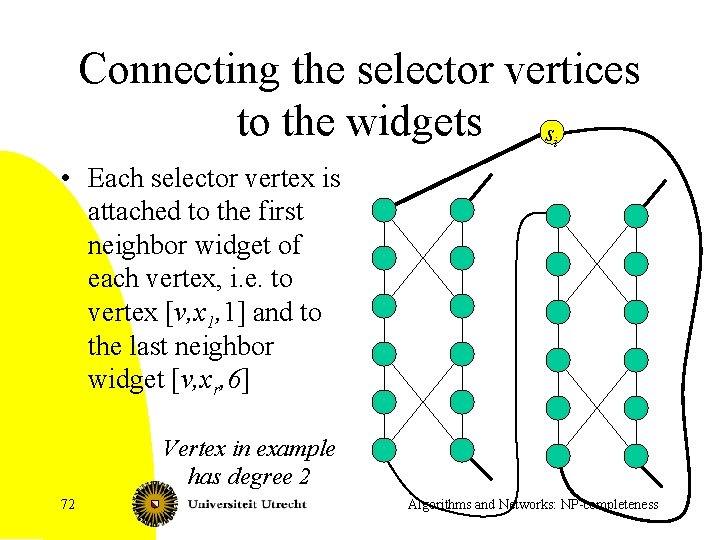
Connecting the selector vertices to the widgets s i • Each selector vertex is attached to the first neighbor widget of each vertex, i. e. to vertex [v, x 1, 1] and to the last neighbor widget [v, xr, 6] Vertex in example has degree 2 72 Algorithms and Networks: NP-completeness

Correctness of reduction • Lemma: G has a vertex cover of size (at most) k, if and only if H has a Hamiltonian circuit. 73 Algorithms and Networks: NP-completeness

Finally • The reduction takes polynomial time. • So, we can conclude that Hamiltonian Circuit is NP-complete. 74 Algorithms and Networks: NP-completeness

TSP • NP-completeness of TSP by local replacement: – In NP. – Reduction from Hamiltonian Circuit: • • Take city for each vertex Take cost(i, j) = 1 if {i, j} Ï E Take cost(i, j) = 0, if {i, j} E G has HC, if and only if there is a TSP-tour of length 0. • Remark: variant with triangle inequality: use weights 2, 1 and n 75 Algorithms and Networks: NP-completeness

10 Weak and strong NP-completeness Algorithms and Networks: NP-completeness

Problems with numbers • Strong NP-complete: – Problem is NP-complete if numbers are given in unary • Weak NP-complete: – Problem is NP-complete if numbers are given in binary, but polynomial time solvable when numbers are given in unary 77 Algorithms and Networks: NP-completeness

Examples • Subset-sum – Given: set of positive integers S, integer t. – Question: Is there a subset of S with total sum t? • Weak NP-complete. (Solvable in pseudo-polynomial time using dynamic programming: O(nt) time…) • 3 -Partition – Given: set of positive integers S, (integer t). – Question: can we partition S into sets of exactly 3 elements each, such that each has the same sum (t)? • Strong NP-hard. • t must be the sum of S divided by |S|/3 = number of groups • Starting point for many reductions 78 Algorithms and Networks: NP-completeness

Remark • Easily made mistake: reductions from subset sum that create exponentially large instances • Subgraph Isomorphism for degree 2 graphs – Given: Graphs G and H, such that each vertex in G and H has degree at most 2 – Question: Is G a subgraph of H? • NP-hardness proof can be done with 3 -PARTITION 79 Algorithms and Networks: NP-completeness

Subgraph isomorphism forests • Input: Forest F =(V, E), forest H = (W, F) • Question: Is there an injection f: W -> V, such that for all {v, w} in F, {f(v), f(w)} is in E, i. e. , is H isomorphic to a subgraph of F? • Theorem: Subgraph isomorphism forests is NP-complete 80 Algorithms and Networks: NP-completeness

Proof • In NP • NP-complete: transform from 3 -partition • Suppose we have numbers a(1), …, a(3 m) with total sum mt. • F is forest with m paths, each with t vertices • H is forest with 3 m paths, with lengths a(1), …, a(3 m) 81 Algorithms and Networks: NP-completeness

11 Some discussion

How to prove NP-completeness • Is there an easy proof by reduction? • Is there a problem that “looks like our problem” – try to do local replacement • Try component design: – Good starting problems are: 3 -Sat; special cases of 3 -sat; 3 -partition; subset sum; simple graph problems (like clique, IS, VC, Coloring) – … puzzle … 83 Algorithms and Networks: NP-completeness

Discussion • Is P ¹ NP? (who thinks so? ) • www. claymath. org/prizeproblems/pvsnp. htm : one of the millennium problems • Why so hard to prove? P • What to do with problems that are NPNP NP-complete? complete • Other complexity notions… 84 Algorithms and Networks: NP-completeness

P vs NP is hard to prove • P = NP? Hard to design poly algorithm. . . • Current mathematical knowledge does not suffice to prove P != NP: – “Natural Proofs” can not separate P from NP (Razborov & Rudich, 1993) – PA = NPA, but PB != NPB for some oracles A and B, so diagonalisation can not separate P from NP (Baker, Gill, & Solovay, 1975) 85 Algorithms and Networks: NP-completeness

12 A Few Animals from The Complexity Zoo

Much more classes • In Theoretical Computer Science, a large number of other complexity classes have been defined • Here, we give an informal introduction to a few of the more important ones • There is much, much more… 87 Algorithms and Networks: NP-completeness

co. NP • Complement of a class: switch “yes” and “no” • co. NP: complement of problems in NP, e. g. : NOT-HAMILTONIAN – Given: Graph G – Question: Does G NOT have a Hamiltonian circuit UNSATISFIABLE – Given: Boolean formula in CNF – Question: Do all truth assignments to the variable make the formula false? 88 Algorithms and Networks: NP-completeness

PSPACE • All decision problems solvable in polynomial space • Unknown: is P=PSPACE? • Savitch, 1970: PSPACE = NPSPACE – NPSPACE: solvable with non-deterministic program in polynomial time • PSPACE-complete, e. g. , – generalized Tic-Tac-Toe, generalized Reversi, – Some puzzles that need an exponential number of moves – Quantified Boolean formula’s (QBF): 89 Algorithms and Networks: NP-completeness

EXPTIME • Decision problems that can be solved in exponential time • P is unequal EXPTIME (Stearns, Hartmanis, 1965) • EXPTIME complete problems: – Generalized chess, generalized checkers, generalized go (Japanese drawing rule) – Given a Turing Machine M and integer k, does M halt after k steps? 90 Algorithms and Networks: NP-completeness

And a few more • NEXPTIME: non-deterministic exponential time • EXPSPACE = NEXPSPACE: exponential space 91 Algorithms and Networks: NP-completeness

Graph Isomorphism • Discussed in another lecture • Given two graphs, are they isomorphic? • In NP, not known to be NP-complete; not known to be in P • Several problems are equaly hard: Isomorphism-complete 92 Algorithms and Networks: NP-completeness

NC • NC: “Nicks class”, after Nick Pippinger • Talks about the time to solve a problem with a parallel machine • Model: we have a polynomial number of processors, that use the same memory – Variants depending on what happens when processors try to read or write the same memory location simultaneously 93 Algorithms and Networks: NP-completeness

NC – the definition • NC: decision problems that can be solved with a PRAM (Parallel Random Access Machine) with polynomial number of processors in polylogarithmic time – O( (log n)d) for some constant d • Unknown: P=NC? • P-complete problems are expected not to be in NC. An example is – Linear Programming (formulated as decision problem) 94 Algorithms and Networks: NP-completeness

Counting • #P: (“Sharp-P”) • Problems that outputs a number • The precise definition will not be given here. Think as: “what is the number of certificates for this instance”, with polynomial checking of certificates • #P-complete e. g. : – Number of satisfying truth assignments of 3 SAT-formula – Number of Hamiltonian circuits in a graph – Number of perfect matchings in a given graph • PP is a related class (vaguely: “decide if the number of solutions is at most given number k”) 95 Algorithms and Networks: NP-completeness

On PP and #P • Inference: – Given: probabilistic network, observations O, variable X, value x, value p in [0, 1] – Question: Pr(X = x | O ) <= p? • Decision variant of problem from course Probabilistic Reasoning • Is PP-complete; variants are #P-complete • PP-hard and #P-hard problems are probably not polynomial. . . 96 Algorithms and Networks: NP-completeness

LSPACE or L • Problems can be solved with only logarithmic extra space: – You can read the input as often as you want – You may use only O(log n) extra memory • E. g. : Q(1) pointers to your input • NL: non-deterministic logspace. . . 97 Algorithms and Networks: NP-completeness

More • The Polynomial Time Hierarchy • Oracles • UP: unique solutions 98 Algorithms and Networks: NP-completeness